4. Распределение Эрланга. Является результатом суммирования целого числа независимых и одинаково распределенных экспоненциальных СВ. Используется в теории массового обслуживания, когда исследуется выполнение работ в течение экспоненциально распределенных промежутков времени.
5. Распределение Пуассона.
Является
дискретным и обычно связано с числом результатов за определенный период
времени. Если продолжительность интервалов времени между результатами
распределена экспоненциально и в каждый момент времени может произойти только
один результат, то число результатов на фиксированном интервале времени
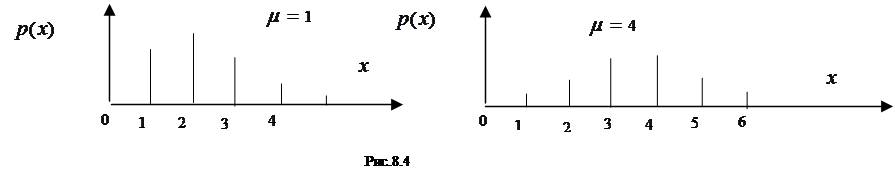
распределено по закону Пуассона. При больших значениях ![]() пуассоновское распределение
аппроксимируется нормальным законом (рис.8.4):
пуассоновское распределение
аппроксимируется нормальным законом (рис.8.4):
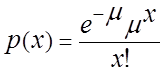 ;
; ![]() ,1,2… ;
,1,2… ; ![]() =
= ![]() ;
;
 |
|||||||
|
|||||||
|
|||||||
|
|||||||
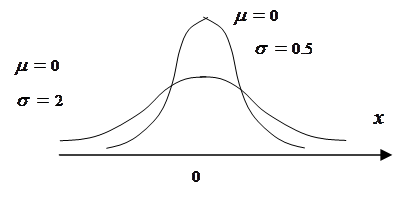
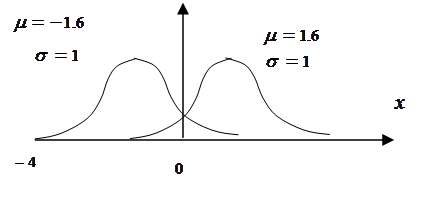
6. Нормальный (гауссовский) закон (рис.8.5):
![]() =
= 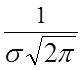 exp
exp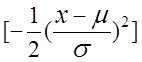 .
.
|
|
 |
|||||
 |
|||||
|
|||||
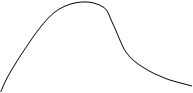
7. ![]() (хи-квадрат)-распределение (рис.8.6).
Пусть
(хи-квадрат)-распределение (рис.8.6).
Пусть ![]() ,…,
,…,![]() -
независимые СВ (например, стаж работы
-
независимые СВ (например, стаж работы ![]() любых
сотрудников учреждения) и
любых
сотрудников учреждения) и ![]() Î
Î ![]() , где
, где ![]() означает нормальное распределение
переменной
означает нормальное распределение
переменной ![]() (величина стажа) признака
(величина стажа) признака ![]() (стажа) в генеральной совокупности
(все сотрудники учреждения);
(стажа) в генеральной совокупности
(все сотрудники учреждения); ![]() ,
, ![]() - параметры распределения. Тогда
распределение величины
- параметры распределения. Тогда
распределение величины
![]()
![]() =
= ![]()
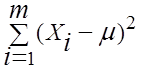
![]()
|
|
![]()
|
|
распределения равна ![]() (вероятность),
(вероятность),
называется квантилем ![]() (условный порог
(условный порог
значимости). С учетом ![]() удобнее записывать квантиль
удобнее записывать квантиль
![]() как
как
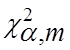 или
или ![]() (
(![]() ) (иногда вместо
) (иногда вместо ![]() употребляют выражение 1-
употребляют выражение 1-![]() ).
).
8.
Распределение Стьюдента (![]() -распределение)
- рис.8.7. Распределение Стьюдента в общем случае оценивает разность между
средними значениями двух независимых нормально распределенных величин
-распределение)
- рис.8.7. Распределение Стьюдента в общем случае оценивает разность между
средними значениями двух независимых нормально распределенных величин ![]() и
и ![]() ,
где
,
где ![]() ,
, ![]() -
объемы выборок соответственно для
-
объемы выборок соответственно для ![]() и
и ![]() :
:
|
|
|
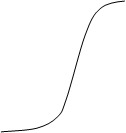

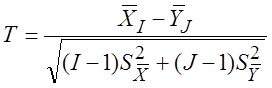
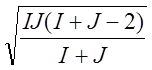 .
.
Число степеней свободы в данном случае
![]()
![]()
![]()
![]()
![]() =
=![]() +
+![]() -2.
Квантиль
-2.
Квантиль ![]() =
= ![]() (
(![]() ) - это значение
) - это значение ![]() ,
,
|
|
|
часто пишут ![]() /2 ).
/2 ).
|
![]() =
= 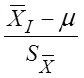
также подчиняется ![]() -распределению. Здесь
-распределению. Здесь ![]() = (
= (![]() -1).
-1).
8.4. ГЕНЕРАЦИЯ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
Наиболее часто применимым на практике методом получения СВ являются генерация одной или нескольких СВ, равномерно распределенных на интервале [0,1] (базовая СВ или БСВ), и последующее преобразование БСВ в новую СВ, распределенную по нужному закону.
Из всех методов получения
СВ предпочтение отдается применению рекурсивных формул, по которым на основании
![]() -й СВ вычисляется (
-й СВ вычисляется (![]() +1)-я СВ. Наилучшим образом
требованиям СВ удовлетворяет конгруэнтный метод:
+1)-я СВ. Наилучшим образом
требованиям СВ удовлетворяет конгруэнтный метод:
![]() = (
= (![]()
![]() +
+![]() )
)![]() ,
, ![]() =0,1,2,…,
=0,1,2,…,
![]() =
= ![]() /
/![]() ,
,
где ![]() ,
, ![]() ,
, ![]() -
константы;
-
константы; ![]() - ненормализованная СВ;
- ненормализованная СВ; ![]() - нормализованная СВ в интервале [0,1]; (
- нормализованная СВ в интервале [0,1]; (![]()
![]() +
+![]() )
)![]() означает, что
означает, что
![]() = (
= (![]()
![]() +
+![]() )
-
)
- ![]() {
{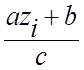 },
},
где {} -
целая часть; ![]() =
=![]() -
корень. Числа
-
корень. Числа ![]() являются не точно
случайными (псевдослучайными) и могут повторяться (имеют период числового
ряда). Для данных конгруэнтных генераторов полный период
являются не точно
случайными (псевдослучайными) и могут повторяться (имеют период числового
ряда). Для данных конгруэнтных генераторов полный период ![]() (
(![]() -
разрядность ЭВМ) соответствует
-
разрядность ЭВМ) соответствует ![]() =
=![]() ,
, ![]() -
простое к
-
простое к ![]() число (наибольший общий делитель
равен 1),
число (наибольший общий делитель
равен 1), ![]() =1+4
=1+4![]() ,
где
,
где ![]() - целое число.
- целое число.
Для параллельных
случайных потоков можно использовать один и тот же генератор с разными ![]() .
.
Фундаментальным методом
получения СВ с заданным законом распределения ![]() является
метод обратной функции:
является
метод обратной функции:
![]() =
= ![]() ,
,
где ![]() -
БСВ,
-
БСВ, ![]() - функция от
- функция от ![]() ,
вычисляемая из уравнения
,
вычисляемая из уравнения
![]() =
= ![]() .
.
Если функцию ![]() найти не удается, используют
процедуры (программы) случайной выборки:
найти не удается, используют
процедуры (программы) случайной выборки:
1) равномерное распределение:
![]() =
= ![]() ;
;
2) треугольное распределение:
![]() =
= ![]() ;
;
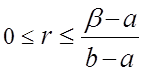 ,
,
![]() =
= ![]() ;
;
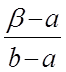 <
<![]() £
1;
£
1;
3) экспоненциальное распределение:
![]() =
= ![]() ;
;
4)
распределение Пуассона: найти первое значение ![]() ,
когда
,
когда
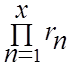 ³
³
![]() >
>
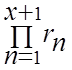 ;
;
5) нормальное
распределение (процедура RNORM(![]() ):
а)
):
а) ![]() -1 б)
-1 б) ![]() -1
в)
-1
в) ![]() г) если
г) если ![]() >1, повторить а,….; если
>1, повторить а,….; если ![]() £1,
то генерация парами:
£1,
то генерация парами: ![]() =
=![]() ;
;
![]() =
=![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.