Приборы и устройства для формирования видимого изображения: Учебное пособие, страница 10

Траекторный пробег вычисляется, согласно классическим представлениям, по формуле:

                 ,                                                           (2.2)

где  - атомный номер материала в таблице Менделеева,  - концентрация атомов в твердом теле (5×10²² ат/см³), - диэлектрическая постоянная, - заряд электрона.

Значения глубины полной диффузии Х_Д и диффузионного радиуса  достаточно просто определяются в модели Арчарда, которую иллюстрирует рис. 2.1.

Феноменологическая модель Арчарда  предполагает, что электроны сначала проходят некоторый путь Х_Д без рассеяния, а затем изотропно (диффузно) рассеиваются. Для случая когда диаметр меньше величины проекционного пробега , поглощение энергии происходит в сфере радиусом :

                          ,                                                     (2.3)

                          .                                                (2.4)

Распределение электронов по глубине при  можно найти по формуле Ленарда:

                      ,                                               (2.5)

где - количество электронов у поверхности.

Потери энергии, вызванные всеми типами неупругих процессов, удобно описывать уравнением, предложенным Бете:

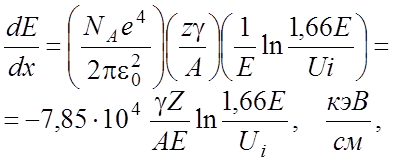                                                      (2.6)

где Е - энергия электрона, кэВ;   - длина пути, см; U_i - средний потенциал (энергия) ионизации,  кэВ.

Так как катодолюминофоры представляют собой многокомпонентные соединения, то при анализе движения электронов  необходимый для расчета эффективный атомный номер определяется из соотношения:

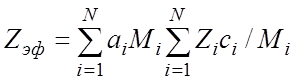                      ,                                              (2.7)

где 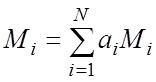,  - атомная концентрация элемента, - атомная масса, - массовая концентрация элемента, 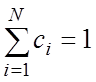, - число компонентов.

Расчеты по формулам показывают , что при энергиях в единицы и десятки кэВ глубина проникновения электронов в твердое тело и область выделения энергии составляет единицы мкм.

Знание глубины проникновения и закономерностей выделения энергии позволяет рекомендовать толщину слоя люминофора. С одной стороны, она должна быть не менее рассчитанной, а с другой – избыточная толщина приводит к уменьшению прозрачности слоя и потере излучения. Кроме того, при разных способах нанесения (пульверизация, трафаретная печать или иной способ)  слой имеет разную шероховатость, разную площадь поверхности, плотность, проводимость, теплопроводность и т.п. Поэтому на практике толщина подбирается эмпирически. Установлено, что одним из самых лучших является метод электрофоретического нанесения из органических суспензий порошка кристаллофосфора. Хорошие результаты получены и при использовании трафаретной печати.

Экстраполяция приведенных выше зависимостей на энергии в (10-100) эВ позволяет считать, что глубина проникновения  должна быть соизмеримой с межатомными расстояниями. Прямые эксперименты подтверждают, что по порядку значений глубины проникновения медленных электронов составляют  сотые и тысячные доли микрометра. Поэтому при ВВК основная доля электронных возбуждений происходит в объеме кристалла люминофора, а при НВК зона непосредственного возбуждения охватывает лишь несколько приповерхностных атомных слоев, хотя миграция генерируемых здесь дырок и электронов расширяет зону свечения за пределы непосредственного возбуждения.

Кроме того, условный квантовый выход ВВК на 2..4 порядка больше, чем НВК. Это обусловлено тем, что один электрон с энергией порядка 10 кэВ может возбудить несколько тысяч квантов излучения с энергией около 3 эВ. Все это приводит к тому, что для достижения одинаковой яркости свечения в устройствах НВК необходимо обеспечить среднюю плотность тока на люминофор на 2-4 порядка больше, чем при ВВК. Так как при малых напряжениях коэффициент вторичной электронной эмиссии у подавляющего большинства веществ меньше единицы, то при НВК люминесцентный слой должен иметь достаточно высокую электропроводность и располагаться на токопроводящей подложке.

Существенно различаются также функции возбуждения при ВВК и НВК. Для  ВВК обычно используется функция следующего вида:

                                         ,                                     (2.8)                               

где - ²мертвый² потенциал, определяемый энергией, затрачиваемой  бомбардирующим электроном на то, чтобы пробиться через малоактивную приповерхностную зону и достигнуть нормально люминесцирующих областей кристалла; - плотность тока; - постоянная, характеризующая данный кристаллофосфор; - коэффициент нелинейности.

Экспериментальные исследования ВВК для катодолюминофора ZnO×Zn дают значения ²мертвого² потенциала 10..20 эВ, а величины =1,5. Для ZnS×Ag  соответственно 50..500 В и =1,6..1,8.

Экспериментальные исследования закономерностей НВК на примере ZnO×Zn показали, что описать функцию возбуждения одним уравнением во всем интервале малых энергий не удается. Однако с точностью, достаточной при практическом применении эффекта в технике, может быть использована следующая  зависимость, справедливая при напряжениях 10100 эВ:

                                                 .                                            (2.9)

2.1. Высоковольтные катодолюминесцентные индикаторы

и  УОИ на их основе

К индикаторам этого типа относят чёрно-белые и цветные кинескопы, осциллографические трубки, электронно-оптические преобразователи и другие приборы. В настоящее время именно цветные кинескопы являются наиболее широко применяемым типом индикатора для телевизоров, терминалов ЭВМ, автоматизированных систем разного назначения.

Современный цветной кинескоп - это сложный электровакуумный прибор, основными элементами которого являются следующие:

-стеклянный корпус (колба), в котором создан и поддерживается вакуум (10^-4 -10^-5 ) Па,

-катодолюминофоры основных цветов, нанесённые на внутреннюю поверхность экрана, преобразующие энергию электронного пучка в видимое излучение соответствующего цвета,

-электронно-оптическая система с тремя (или одной) электронными пушками с оксидным катодом, формирующая электронные пучки и ускоряющая электроны до энергий 25-30 кэВ,