Преобразование сигналов измерительной информации: Методические указания к лабораторным работам

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ 

АКАДЕМИЯ

ПРЕОБРАЗОВАНИЕ

 СИГНАЛОВ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ

Методические указания  к лабораторным работам

Рязань 2005

УДК 681.317.3

       Преобразование  сигналов измерительной информации: Методические указания  к лабораторным работам  /   Рязан.  гос.  радиотехн. акад. / Сост.

Г.А. Садовский.  Рязань, 2005. 16 с.  

         Изучаются представление периодических сигналов  рядом Фурье, интеграл Фурье, преобразование сигналов в линейных цепях (амплитудные и фазовые искажения сигналов прямоугольной и треугольной формы), рассматриваются спектры модулированных сигналов (АМ, ЧМ, ФМ, АИМ, ШИМ, ЧИМ).

         Предназначено для студентов специальностей 1906 ”Инженерное дело в медико-биологической практике” и 1909 ”Информационно-измерительная техника и технологии”.

      Библиогр.: 9 назв.

     Частота, амплитуда, фаза, спектр, преобразование, синтез частотные, фазовые  искажения, модуляция, демодуляция, глубина модуляции, индекс модуляции.

           Печатается по решению методического совета Рязанской государственной радиотехнической академии.

              Рецензент:  кафедра информационно-измерительной и биомедицинской техники РГРТА  (зав. кафедрой  доцент  В.И.Жулев ).

Преобразование сигналов измерительной информации

Составитель С а д о в с к и й Гардон Антонович

Редактор   Е.В.Игнатова

Корректор С.В.Макушина

Подписано в печать   06.05.05.   Формат бумаги 60х84 1/16.

Бумага газетная.   Печать трафаретная.    Усл.  печ. л. 1.0

Уч.-изд. л.1.0.   Тираж  30 экз.  Заказ         .  

Рязанская государственная радиотехническая академия.

390005, Рязань, ул. Гагарина, 59/1.

Редакционно-издательский центр РГРТА.

 Лабораторная работа № 1.  Преобразование сигналов в линейных цепях

    Цель работы: изучение ортогонального представления сигналов, анализ и синтез сигналов рядом Фурье, преобразование сигналов в линейных цепях, амплитудные и фазовые искажения сигналов.

1.  Теоретическая часть

1.1 . Спектры периодических сигналов.  Ряд Фурье

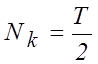         Для описания периодических сигналов широко используется ортогональная система тригонометрических функций  Тригонометрические функции ортогональны на периоде  основной частоты  Норма тригонометрических функций :     при                                 при               

         Описание сигналов тригонометрическими функциями называется обобщенным рядом Фурье  и представляет собой разложение  сигнала на спектральные составляющие: 

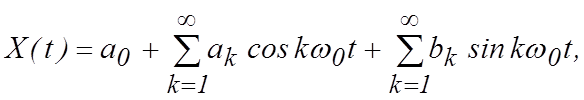                           (1.1.1)

где    - постоянная составляющая (среднее значение) сигнала, и        - амплитуды соответственно косинусной и синусной составляющих -й гармоники основной частоты.

      Коэффициенты разложения определяются интегралом по периоду

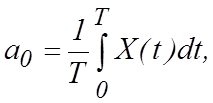
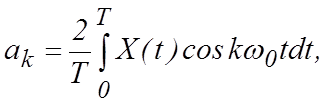
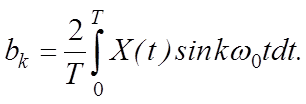      (1.1.2)

        Косинусные и синусные составляющие в (1.1.1) можно объединить. Тогда ряд Фурье принимает вид

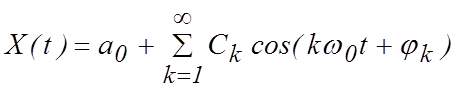         ,                                     (1.1.3)

где   и   – соответственно амплитуда  и начальная фаза  -й гармоники.

   Разложив косинус суммы  в (1.1.3), получаем

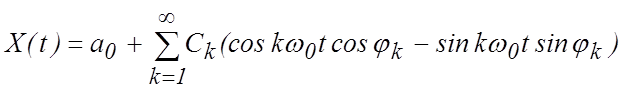.                       (1.1.4)

   Отсюда находим

       

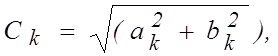
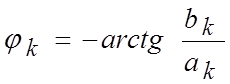                    _.                      (1.1.5)

   Ряд Фурье в комплексной форме принимает вид

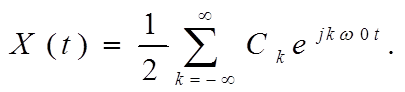                                                      (1.1.6)

    Значения комплексных коэффициентов Фурье

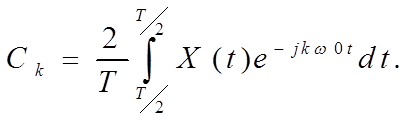                             (1.1.7)

        Соотношения (1.1.6 )  и  (1.1.7 ) образуют пару преобразования Фурье (прямое и обратное) для периодических сигналов.

       Особенности представления сигналов рядом Фурье

1.  Спектр периодических сигналов дискретный.

2.  Расстояние между спектральными составляющими равно частоте  периодической последовательности сигналов.

3.  Математический спектр простирается по всей оси частот от минус до плюс бесконечности.

4.  Физический спектр имеет место на положительной полуоси частот (физически невозможно определить отрицательные частоты).

5.  Размерность спектральных коэффициентов совпадает с размерностью представляемой физической величины.

6.  Амплитудный спектр – четная функция частоты.

7.  Фазовый спектр – нечетная функция частоты.

1.2. Спектры одиночных сигналов.  Интеграл Фурье

        Одиночный, непериодический сигнал можно представить в виде периодической последовательности с периодом следования не меньшим длительности сигнала и разложить его в ряд Фурье согласно (1.1.7).  Если непрерывно увеличивать период следования в пределе до бесконечности, то получается одиночный сигнал. При этом расстояние между спектральными составляющими стремится к нулю. Следовательно, спектр такого сигнала становится сплошным. С ростом периода ( → ∞ )  приращение частоты  стремится к бесконечно малой величине  :  → .       Частота близко стоящих гармоник переходит текущее значение непрерывной частоты: .  Дискретнаясумма    заменяется интегралом. Подставив значение комплексных коэффициентов    ,           умножив и разделив на   с   учетом сформулированных положений  и   → ∞ выражение  (1.1.7)  принимает вид

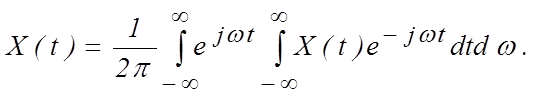                             (1.2.1)

        Внутренний интеграл имеет размерность преобразуемой физической величины, умноженную  на размерность времени или деленную на размерность частоты, что отражает значения амплитуд спектральных составляющих, приходящихся на единичную полосу частот. Эта величина называется спектром сигнала, полностью описывает сигнал в частотной области, определяется функциональной зависимостью сигнала от времени и равна   

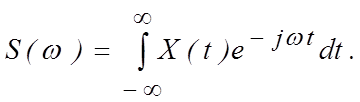                                                  (1.2.2)

     В свою очередь  сигнал, представленный во временной области, полностью определяется своим спектром.  Сигнал формируется непрерывными спектральными составляющими со своими начальными фазами

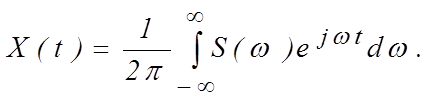                                                         (1.2.3)

     Преобразования  (1.2.2)  и  (1.2.3)  называются парой преобразования Фурье для одиночных сигналов.  Особенности спектров одиночных сигналов.

1.  Спектр одиночных сигналов сплошной (непрерывный) и бесконечный.

2.  Спектр в общем случае является комплексным.

3.  Математический спектр простирается по всей оси частот от минус до плюс бесконечности.

4.  Физический спектр имеет место на положительной полуоси частот.

5.  Размерность спектра одиночных сигналов равна размерности физической       величины, деленной на размерность частоты.

1.3.  Синтез сигналов рядом Фурье

       Периодическая последовательность импульсных сигналов может быть представлена (синтезирована) бесконечной суммой гармоник с амплитудами