Преобразование сигналов измерительной информации: Методические указания к лабораторным работам, страница 2

 и фазовыми сдвигами   

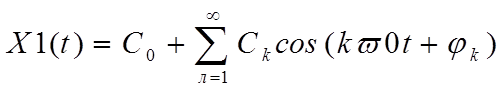                .                                 (1.3.1)

     Коэффициенты  - вещественные амплитуды гармоник с их знаками – можно вычислить по спектрам одиночных сигналов:

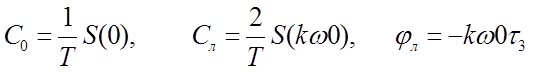,                      (1.3.2)

где    - запаздывание (смещение) центра сигналов относительно начала координат , равное  в конкретном случае половине длительности импульсов.

        Спектры одиночных прямоугольного и треугольного импульсов амплитудой  и длительностью  соответственно равны

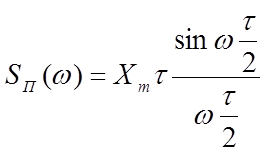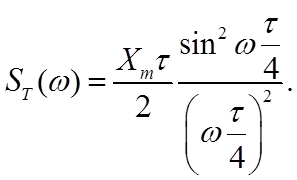 ;                          (1.3.3)        

           1.4.  Преобразование сигналов в линейных цепях

Амплитудные и фазовые искажения в линейных цепях определяются их амплитудно-частотной (частотной)  и фазочастотной (фазовой)  характеристиками.  Амплитуды  k-х гармоник изменяются в  раз, а начальные фазы смещаются на . Следовательно, на выходе линейной цепи получаем  новые значения амплитуд гармоник и фазовых сдвигов: . Синтезируемый сигнал принимает вид

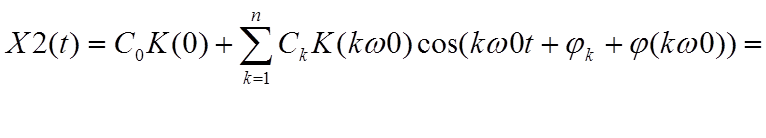
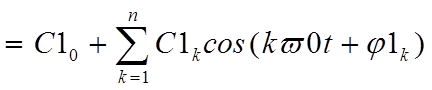.                          (1.4.1)

Частотная и фазовая характеристики линейных цепей первого порядка

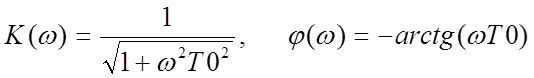,                    (1.4.2)

где Т0 – постоянная времени цепи.

2.  Моделирование искажений сигналов в линейных цепях

1.  Установить параметры (целесообразно нормированные) прямоугольного и треугольного сигналов, расположенных в начале координат (при t=0): амплитуда А=1, период следования Т=1, длительность t в пределах (0.1….0.5)Т. При этом следует иметь ввиду, что в описании представлены формулы, а не операторы системы.

2.  Ввести спектры прямоугольного и треугольного сигналов согласно (1.3.3).

3.  Задать число определяемых гармоник в пределах .

4.  Рассчитать вещественные значения коэффициентов Фурье   и начальные фазы (амплитуды   гармоник и их  фазовые сдвиги, k=0…n) для прямоугольного и треугольного сигналов:

,

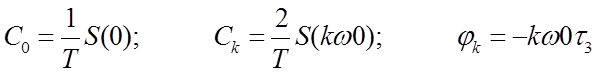где  - смещение (запаздывание) центра сигналов относительно начала                  координат (t=0), равное в данном случае половине длительности импульсов.

5.  Построить гистограммы массивов коэффициентов  и фаз .

6.  Синтезировать сигнал рядом Фурье:

.

7.  Синтезировать сигнал на выходе линейной цепи:  

.

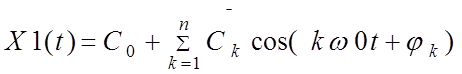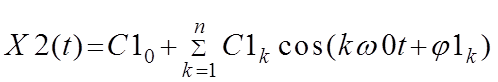8.   Синтезировать сигнал на выходе линейной цепи при равной нулю фазовой характеристики цепи  с целью оценки амплитудных искажений:

.    

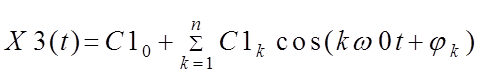9.   Синтезировать сигнал на выходе линейной цепи при постоянном коэффициенте передачи  ( и наличии  только фазовых сдвигов в цепи   с целью оценки фазовых искажений:

.      

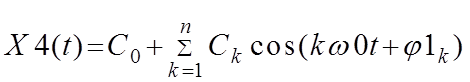10.  Построить графики и сравнить исходные и синтезированные сигналы  

      при разных значениях числа гармоник.

11.   Рассчитать погрешности  (дисперсии и средние квадратические

  отклонения) синтезированного сигнала  на выходе цепи.  Общая   

       расчетная формула для оценки погрешностей

.

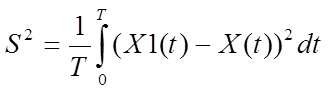12.   Изменяя длительности импульсов и постоянную времени цепи изучить

       зависимости искажений от сигналов от  параметров цепи.

13.  Повторить анализ преобразования, амплитудных и фазовых искажений 

сигналов в линейной цепи второго порядка при различных значениях     собственной частоты   и степени затухания :

.

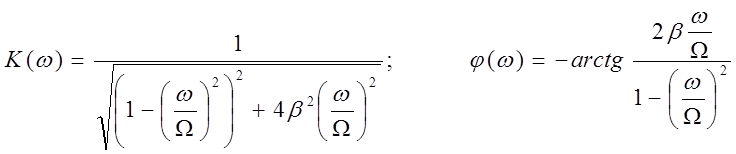Контрольные вопросы

1.  Ортогональные и ортонормированные системы базисных функций. Типовые системы ортогональных функций.

2.  Представление сигналов ортогональными системами функций и определение коэффициентов.

3.  Представление сигналов рядом и интегралом Фурье. Области применения.

4.  Принцип построения спектральных диаграмм базисных функций.

5.  Основные принципы анализа и синтеза сигналов.

6.  Частотные и фазовые характеристики линейных цепей.

7.  Оценка амплитудных и фазовых искажений сигналов в линейных цепях.

Библиографический список

1.  Баскаков С.И.  Радиотехнические цепи и сигналы. М.: Высшая школа, 1988. С. 38-55, 184-202.

2.  Гоноровский И.С.  Радиотехнические цепи и сигналы. М.: Радио и связь, 1986.     С. 16-67.

3.  Гутников В.С.  Фильтрация измерительных сигналов.

     Л.: Энергоатомиздат, 1990.

4.  Двайт Г.Б. Таблицы интегралов и другие математические формулы.

     М.: Наука, 1978.

5.  Орнатский П.П. Теоретические основы информационно-измерительной техники. Киев: Вища школа, 1983. С. 190-197.

6.  Садовский Г.А. Аналитическое описание сигналов. Рязань:  РРТИ,1987.

7.  Харкевич А.А. Спектры и анализ. М.: Физматгиз, 1962. С. 9-33.

Лабораторная работа №2.  Спектры модулированных сигналов

1. Теоретическая часть

1.1.   Модуляция и демодуляция

        Для передачи измерительной информации параметры сигнала-носителя подвергаются модуляции. Процесс управления (изменения) параметров несущего сигнала в соответствии со значением измеряемой (передаваемой, преобразуемой) величины называется модуляцией, управляющая величина - модулирующей, а сигнал-носитель - модулированным. Если модуляции подвергается только один параметр сигнала-носителя, имеет место однопараметрическая модуляция, в противном случае – многопараметрическая. Преобразователи, в которых осуществляется модуляция сигнала, называются модуляторами. Выделение модулирующей функции из модулированного сигнала – демодуляция, а преобразователи модулированного сигнала в модулирующий называются демодуляторами.

    Непрерывный гармонический сигнал-носитель описывается функцией

где амплитуда, круговая (угловая) частота (циклическая частота, период),  начальная фаза – постоянные параметры гармонического сигнала. Изменению (модуляции) могут подвергаться амплитуда амплитудная модуляция  (АМ), частота  частотная модуляция  (ЧМ),   фаза  фазовая модуляция  (ФМ).

При импульсном сигнале-носителе параметрами являются амплитуда  длительность импульсов  частота следования  или период  положение импульсов относительно тактовых сигналов и др. Модуляция одного из параметров приводит к амплитудно-импульсной (АИМ), широтно-импульсной  ( ШИМ)  и частотно-импульсной  (ЧИМ)  модуляциям. Возможны и другие виды модуляции: фазоимпульсная  (ФИМ),  кодо-импульсная  (КИМ) и т.д.

1.2.   Амплитудная модуляция

         При амплитудной модуляции (АМ) под действием управляющей функции  изменяется амплитуда гармонического сигнала-носителя в заданных пределах     Отношение изменения к начальному значению амплитуды называется глубиной модуляции:    Аналитическое описание  АМ-сигнала

                               (1.2.1)

При гармонической модулирующей функции   АМ-сигнал имеет вид

                    (1.2.2)

   По формулам преобразования произведения тригонометрических функций в суммы находим

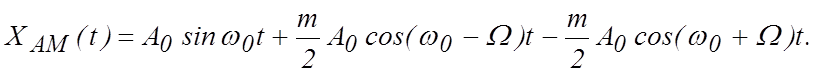     (1.2.3)