Проверил:
проф. Каширин И. Ю.
2010 г.
Введение. 3
Элементы теории. 5
Постановка задачи. 8
Интерфейс разработанной программы. 10
Программа поиска. 12
Поиск в глубину. 13
Поиск в ширину. 15
Поиск по градиенту. 17
Оценка эффективности поиска. 22
Заключение. 24
Искусственный интеллект — это раздел информатики, посвященный моделированию интеллектуальной деятельности человека. Зародившийся более 700 лет назад в средневековой Испании искусственный интеллект оформился в самостоятельную научную область в середине XX в. Пройдя сложный, извилистый путь многократных метаний между чрезмерным оптимизмом и необоснованным скептицизмом, в наши дни искусственный интеллект получил блестящие практические приложения, открывающие перспективы, без которых немыслимо дальнейшее развитие цивилизации.
Методы искусственного интеллекта позволили создать эффективные компьютерные программы в самых разнообразных, ранее считавшихся недоступными для формализации и алгоритмизации, сферах человеческой деятельности, таких как медицина, биология, зоология, социология, культурология, политология, экономика, бизнес, криминалистика и т.п. Идеи обучения и самообучения компьютерных программ, накопления знаний, приемы обработки нечетких и неконкретных знаний позволили создать программы, творящие чудеса. Компьютеры успешно борются за звание чемпиона мира по шахматам, моделируют творческую деятельность человека, создавая музыкальные и поэтические произведения, распознают образы и сцены, распознают, понимают и обрабатывают речь, тексты на естественном человеческом языке. Нейрокомпьютеры, созданные по образу и подобию человеческого мозга, успешно справляются с управлением сложными техническими объектами, диагностикой заболеваний человека, неисправностей сложных технических устройств; предсказывают погоду и курсы валют, результаты голосований; выявляют хакеров и потенциальных банкротов; помогают абитуриентам правильно выбрать специальность и т.д.
Мы уже привыкли к тому, что компьютеры «умнеют» буквально на глазах, а компьютерные программы становятся все более и более интеллектуальными. Само по себе понятие интеллекта постоянно претерпевает изменения по мере развития науки и человека. Давно уже не считаются интеллектуальными задачи, состоящие в выполнении арифметических операций сложения, умножения, деления. Не считается интеллектуальной задача интегрирования дифференциального уравнения, если для нее известен строго детерминированный алгоритм. В настоящее время принято считать интеллектуальными задачи, которые на современном этапе не поддаются алгоритмизации в традиционном смысле этого слова. Это задачи, для решения которых требуются манипуляции с нечеткими, неконкретными, ненадежными, расплывчатыми и даже нетрадиционными знаниями.
В данном курсовом проекте рассмотрен вариант решения такой интеллектуальной задачи, как отыскание роботом пути в лабиринте.
Дерево вариантов – дерево, вершины которого соответствуют ситуациям в предметной области для рассмотрения возможного изменения этих ситуаций для приближения к целевой ситуации.
Целевая ситуация – программная модель ситуации предметной области, которая должна быть достигнута для решения интеллектуальной задачи.
Деревья вариантов делятся на эксплицитные и имплицитные.
Эксплицитным является дерево, все вершины которого заранее известны.
Имплицитным является дерево с известной начальной ситуацией и известной процедурой определения целевой ситуации. Предполагается также, что известна порождающая процедура – это алгоритм порождения дочерней вершины в дереве вариантов (выполнение хода).
В зависимости от представления задачи и способов ее решения различают деревья вариантов в пространстве состояний и деревья вариантов в пространстве задач.
При поиске в пространстве задач вершины соответствуют подзадачам, решение которых необходимо для решения задач более верхнего уровня.
Для поиска в пространстве подзадач характерно применение «И»/»ИЛИ» деревьев. Они состоят из двух типов вершин: И – вершины соответствуют задаче для решения которой необходимо найти решения всех ее подзадач; ИЛИ – вершина соответствует задаче для решения которой необходимо решение хотя бы одной из подзадач.
Для поиска на деревьях вариантов существуют два основных метода: «поиск в глубину» и «поиск в ширину».
Поиск в глубину
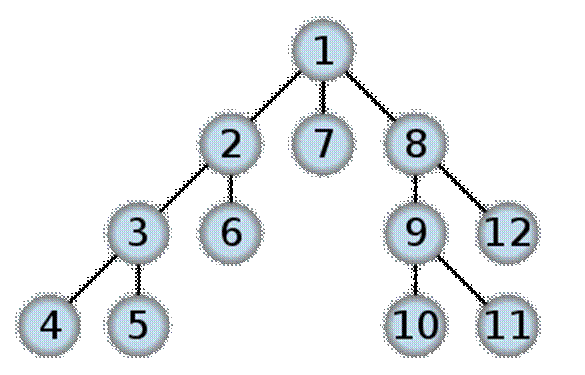
Алгоритм основан на последовательном переборе вариантов. Изменение начальной ситуации начинается каждый раз с самого левого потомка. При этом исследуются дочерние вершины до обнаружения решения (целевой ситуации) или тупика. В случае обнаружения тупика алгоритм реализует возврат к отцовской порождающей вершине и осуществляет попытку рассмотрения очередного варианта. Алгоритм заканчивается при отыскании любой из целевых вершин или при обнаружении ситуации в которой начальная вершина является тупиковой.
Тупиковой называется вершина, относимая к тупиковым соответствующей логической подпрограммой или вершина все потомки которой также тупиковые вершины.
Поиск в ширину
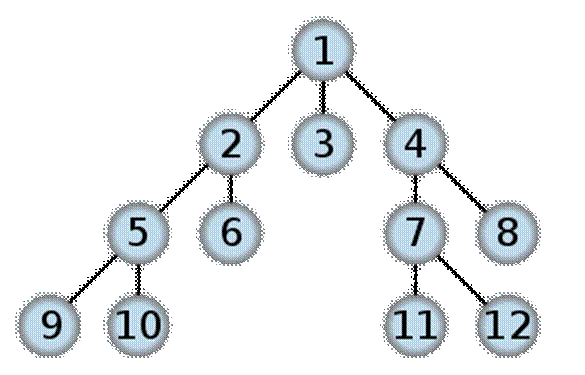
Алгоритм основан на переборе вариантов параллельно во всех возможных направлениях на дереве вариантов. Этот алгоритм исследует сначала вершины уровня 1, затем уровня 2 и т. д., пока не будет найдено ближайшее решение или все тупиковые вершины.
Поиск пути а лабиринте – одна из наиболее распространенных и любимых нами с детства логических задач. Смысл ее состоит в том, чтобы попасть из исходной (начальной) точки в конечную (целевую). Сложность состоит в отыскании пути, т.к. он проходит через хитрый извилистый лабиринт, с множеством тупиков. Ходить можно только в четырех направлениях: верх, низ, лево, право. Человек успешно справляется с этой задачей, целью данного курсового проекта является написание программы (интеллектуального решателя задачи) которая бы наглядным образом показала, как используя стандартные алгоритмы поиска можно искать выход из виртуального лабиринта с помощью ЭВМ.
В данном курсовом проекте задача решалась для поля 16х16 клеток. Для определения местоположения препятствий, а также исходной точки и целевой используется таблица.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.