Интеллектуальные решатели задач (отыскание роботом пути в лабиринте), страница 3

                    if(chStep->Checked)MessageBox::Show("Step " + stepCount.ToString(),"ok");

          }

          if(s == "!") MessageBox::Show("Решение найдено за " + stepCount.ToString() + " шагов!", "=)", MessageBoxButtons::OK, MessageBoxIcon::Information);

          else MessageBox::Show("Решение не найдено!", "=(", MessageBoxButtons::OK, MessageBoxIcon::Information);

                               }

catch(Exception ^ ex)

{

          MessageBox::Show("Ошибка! " + ex->Message, "Внимание!");

}

//Ищем возможные ходы для вершины, заносим их в очередь для поиска в ширину

private: void ScanUseBFS(int i, int j)

{

          stepCount++;

          if(isFinish(i-1, j)) s = "!"; else if(canUse(i-1, j) && s != "!") {mustUse(i-1, j); quI->Enqueue(i-1); quJ->Enqueue(j);}

          if(isFinish(i, j-1)) s = "!"; else if(canUse(i, j-1) && s != "!") {mustUse(i, j-1); quI->Enqueue(i); quJ->Enqueue(j-1);}

          if(isFinish(i+1, j)) s = "!"; else if(canUse(i+1, j) && s != "!") {mustUse(i+1, j); quI->Enqueue(i+1); quJ->Enqueue(j);}

          if(isFinish(i, j+1)) s = "!"; else if(canUse(i, j+1) && s != "!") {mustUse(i, j+1); quI->Enqueue(i); quJ->Enqueue(j+1);}

}

//Закрываем вершину, ищем возможные ходы с занесением их в очередь для поиска в ширину

private: void mustCloseBFS(int i, int j)

                              {

                                         if(!isNotUsed(i, j))

                                        {

                                                   ScanUseBFS(i, j);

                                                   dgv->Rows[i]->Cells[j]->Value = sStep;

                                         }

                              }

Поиск по градиенту

try

{

iIndex = -1;

          s = "";

          stepCount = 0;

          int k;

          k = 0;

          for(k; k < iMax; k++)

          {

                    arI[k,0] = 0;

                    arI[k,1] = 0;

          }

          findStart();

          findFinish();

          ScanUseDFSWithGradient(startI,startJ);

          if(chStep->Checked)MessageBox::Show("Step " + stepCount.ToString(),"ok",MessageBoxButtons::OK);

          while(iIndex >= 0 && s != "!")

          {

                    minGipotenuza();

                    mustCloseGradient(arI[minInd, 0],arI[minInd, 1]);

                    arI[minInd, 0] = 777;

                    arI[minInd, 1] = 777;

          if(chStep->Checked)MessageBox::Show("Step " + stepCount.ToString(),"ok");

          }

          if(s == "!") MessageBox::Show("Решение найдено за " + stepCount.ToString() + " шагов!", "=)", MessageBoxButtons::OK, MessageBoxIcon::Information);

          else MessageBox::Show("Решение не найдено!", "=(", MessageBoxButtons::OK, MessageBoxIcon::Information);

                               }

catch(Exception ^ ex)

{

MessageBox::Show("Ошибка! " + ex->Message, "Внимание!");

}

//Закрываем вершину, ищем возможные ходы с занесением их в массив для поиска по градиенту

private: void mustCloseGradient(int i, int j)

                     {

                               if(!isNotUsed(i, j))

                               {

                                          ScanUseDFSWithGradient(i, j);

                                          dgv->Rows[i]->Cells[j]->Value = sStep;

                               }

                     }

//Ищем возможные ходы для вершины, заносим их в массив для поиска по градиенту

private: void ScanUseDFSWithGradient(int i, int j)

{

          stepCount++;

          if(isFinish(i-1, j)) s = "!"; else if(canUse(i-1, j) && s != "!") {mustUse(i-1, j); arI[++iIndex,0] = i-1; arI[iIndex,1] = j;}

          if(isFinish(i, j-1)) s = "!"; else if(canUse(i, j-1) && s != "!") {mustUse(i, j-1); arI[++iIndex,0] = i; arI[iIndex,1] = j-1;}

          if(isFinish(i+1, j)) s = "!"; else if(canUse(i+1, j) && s != "!") {mustUse(i+1, j); arI[++iIndex,0] = i+1; arI[iIndex,1] = j;}

          if(isFinish(i, j+1)) s = "!"; else if(canUse(i, j+1) && s != "!") {mustUse(i, j+1); arI[++iIndex,0] = i; arI[iIndex,1] = j+1;}

          if(iIndex == -1) iIndex++;

}

Оценка эффективности поиска

Для оценки эффективности анализируют следующие характеристики:

−  время поиска;

−  объем оперативной памяти, занятой программой;

−  активизированное поддерево вариантов – дерево, построенное имплицитно в процессе решения задачи.

Базовые характеристики поиска рассчитываются на основе активизированного поддерева:

−  длина пути решения (L) – число вершин, лежащих на минимальном из найденных путей решения.

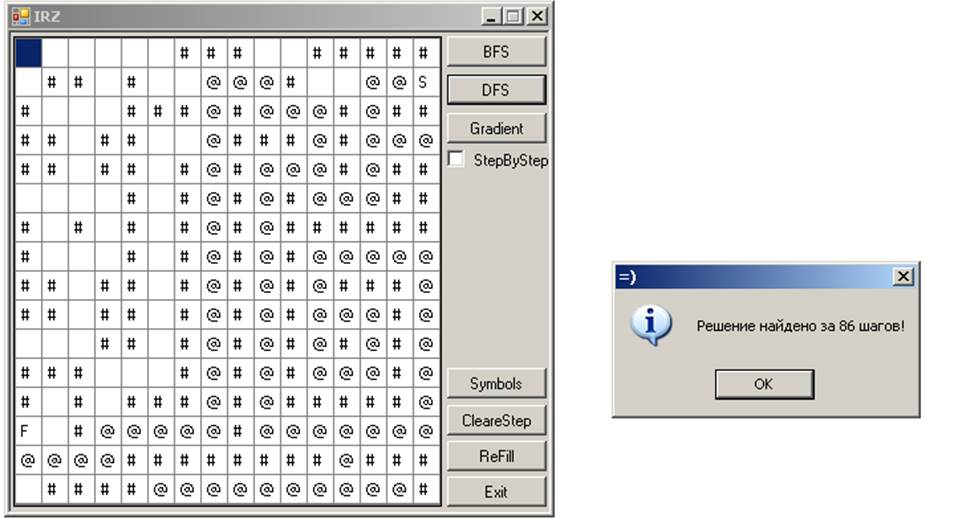
Поиск в глубину: 36

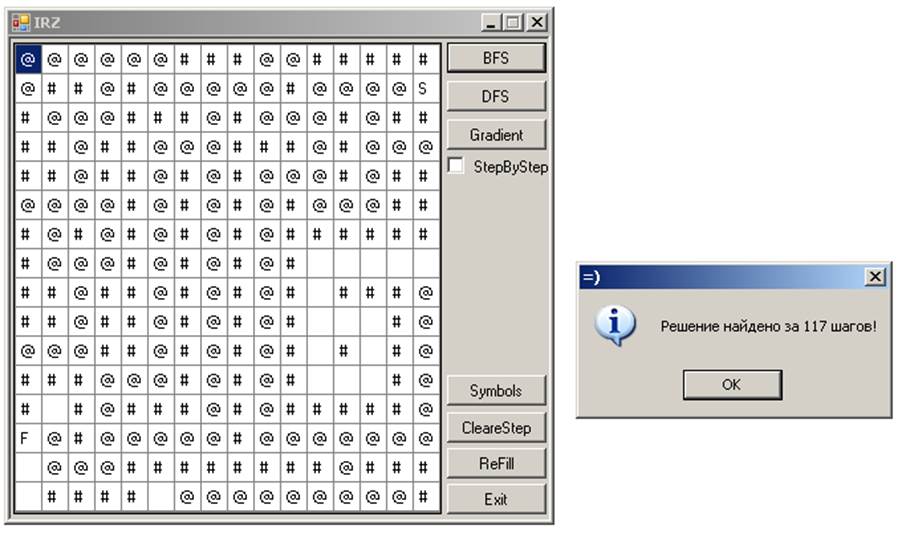
Поиск в ширину: 31

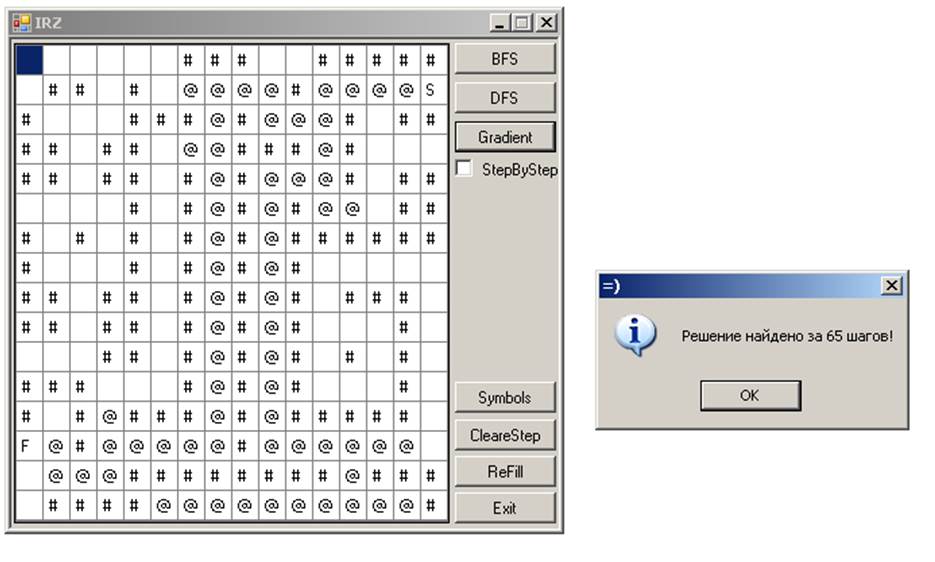
Поиск по градиенту 31

−  общее число порожденных вешин (N)

Поиск в глубину: 86

Поиск в ширину: 117

Поиск по градиенту 65

Производные характеристики поиска рассчитываются на основе базовых:

−  разветвленность поиска

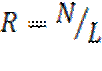
Поиск в глубину: 2,36

Поиск в ширину: 3,77

Поиск по градиенту: 2,09

−  направленность поиска

Поиск в глубину: 1,13

Поиск в ширину: 1,17

Поиск по градиенту: 1,14

Таким образом, поиск по градиенту оказался гораздо более эффективным, чем два других.

Заключение

Из данного курсового проекта стало очевидно, что использование компьютера в качестве интеллектуального решателя задач не только возможно, но и благодаря скорости их решения и простоты используемых алгоритмов весьма целесообразно. Очевидно и то что для сложных и важных задач необходимо применять более точные и быстрые алгоритмы. Так даже на примере данной задачи о поиске роботом пути в лабиринте видно что использование поиска по градиенту дает гораздо лучший результат, нежели остальные два рассмотренных. Я считаю, что подобные технологии в будущем будут востребованы и очень полезны.