Цель работы: Изучение движения тел по наклонной плоскости. В первой части исследуется поступательное движение (скольжение) цилиндра. При этом необходимо экспериментально определить зависимость ускорения от угла наклона плоскости и найти коэффициент трения скольжения. Во второй части изучается движение металлического шарика и определяются условия, при которых возможно движение методом чистого качения и качения со скольжением; по экспериментальной зависимости ускорения шарика от угла наклона плоскости определяется угол, при котором качение переходит в качение со скольжением.
Приборы и принадлежности: макет экспериментальной установки с выбором тел (шарик, цилиндр).
Элементы теории.
При вращении тела вокруг неподвижной оси мгновенная
линейная скорость любой точки этого тела равна ![]() , где
, где ![]() -угловая скорость,
-угловая скорость, ![]() -радиус-вектор, проведенный из оси вращения в данную
точку.
-радиус-вектор, проведенный из оси вращения в данную
точку.
Сложное плоское движение следует рассматривать как сумму двух движений – вращательного вокруг оси, проходящего через центр масс С, и поступательного движения со скоростью Vc центра масс.
![]() (1)
(1)
На рис.2 показан случай, когда скорость Vi в точке А равна скорости Vc движения центра масс:

![]()

![]()
![]() (2)
(2)
 |
|||
Рассмотрим тело, находящееся на наклонной плоскости, составляющей с горизонтом угол а .Если тело скользит по наклонной плоскости, то сила трения равна силе трения скольжения:
![]() (3)
(3)
![]() -
коэффициент скольжения.
-
коэффициент скольжения.
В состоянии покоя векторная сумма всех сил, действующих на тело, равна нулю:
![]() (4)
(4)
Проектируя это уравнение соответственно на оси X и Y, получаем
Fmp.nok= mg sina
![]()
![]()


![]()
При некотором угле наклона ао сила трения Fmp.nok станет равной максимальной силе трения, т.е. силе трения скольжения:
mg sinao= ![]() mg cosao (6)
mg cosao (6)
tgao =![]() . (7)
. (7)
Пи дальнейшем увеличении угла наклона получим:
ma=![]() (8)
(8)
a= g(sina-μcosa) (9)
При качении без скольжения для скорости центра масс тела относительно плоскости можно записать соотношение
Vc=ωR (10)
а= Vc= εR (11)
где ε и ω –угловые ускорение и скорость вокруг оси.
Поскольку тело движется способом качения без скольжения, указанная сила трения покоя подчиняется условию:
Fmp ≤ μmgcosa (12)
ma=![]() (13)
(13)
Используя основной закон динамики вращательного движения, можно записать:
Iε=M (14)
где ε =а/R- угловое ускорение ; I –момент инерции шарика; М=FmpR-момент силы трения.
Проекция ур. (13) на ось X:
Ma=mg sina-Fmp (16)
Из (15) и (16) находим:
a=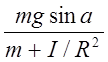
Учитывая, что момент инерции I шарика
относительно оси равен ![]() mR2
, получаем для выражения ускорения :
mR2
, получаем для выражения ускорения :
a=![]() gsina (17)
gsina (17)
получим
Fmp= 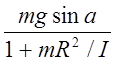 =
=![]() mg sina (18)
mg sina (18)
Теперь из (12) и (18) можно получить условие, при котором возможно качение без скольжения:
или tga<
![]() μ
μ
Зная угол ао , можно оценить величину коэффициента трения скольжения
μ=![]() tg ао(20)
tg ао(20)
Поскольку реальное движение шарика является одновременно и вращательным и скользящим, то значения ускорения должны находиться в пределах
![]() g sina<a<g
sina (21)
g sina<a<g
sina (21)
Расчетная часть.
|
а,градусы |
t1, c |
t2, c |
t3, c |
t4, c |
t5, c |
tcpeдн, c |
а,m/c2 |
|
10 |
|||||||
|
20 |
|||||||
|
30 |
|||||||
|
40 |
|||||||
|
50 |
|||||||
|
60 |
|||||||
|
70 |
|||||||
|
80 |
|||||||
|
90 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.