Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Лабораторная работа № 1-20
«ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ»
Ампилогов Н. В.
Малютин А. Е.
Цель работы: изучение динамики вращательного твёрдых тел; знакомство с методом крутильных колебаний, предназначенным для определение моментов инерции тел.
Приборы и принадлежности: прибор для определения крутильных колебаний – унифилярный подвес ФПМ05, снабженный набором твёрдых тел (грузов) и электронным миллисекундометром.
Для начала запишем уравнение динамики вращательного движения твёрдого тела вокруг неподвижной оси:
1)
![]() где
M – момент действия на тело сил, взятый относительно
оси вращения; J – момент инерции тела вокруг оси вращения;
где
M – момент действия на тело сил, взятый относительно
оси вращения; J – момент инерции тела вокруг оси вращения; ![]() - угловое ускорение тела.
- угловое ускорение тела.
Моментом инерции материальной точки относительно некоторой оси называется величина, численно равная произведению массы тачки на квадрат её расстояния от оси:
2)
![]() .
.
Для протяженных тел момент инерции равен сумме моментов инерции отдельных материальных точек (Dmi) на которые можно разбить данное тело:
3)
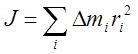 .
.
Когда число элементарных масс стремиться к бесконечности, сума переходит в интеграл:
4)
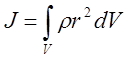 ,
где
,
где ![]() r -
плотность материала; V – объём тела.
r -
плотность материала; V – объём тела.
В данной работе используется система представляющая собой твёрдое тело, подвешенное на струне, закреплённой с обеих сторон. После отклонения бруска на некоторый угол j от положения равновесия и отпускания система начинает совершать свободные крутильные колебания.
Уравнения колебаний данной системы при малых углах отклонения j можно записать так:
5)
![]() ,
,
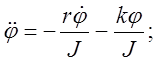
где r
– коэффициент момента сил сопротивления, численно равный моменту сил
сопротивления при угловой скорости ![]() (равной 1 рад/с);
k –
коэффициент возвращающего (упругого) момента, численно равный моменту упругих
сил, возникающих при закручивании струны на угол, равный одному радиану.
(равной 1 рад/с);
k –
коэффициент возвращающего (упругого) момента, численно равный моменту упругих
сил, возникающих при закручивании струны на угол, равный одному радиану.
При малом сопротивлении среды, в которую помещена колеблющаяся система, числовое значение r – пренебрежимо мало.
Предположив, что 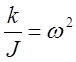 , уравнение (5) можно переписать
следующим образом:
, уравнение (5) можно переписать
следующим образом:
6)
![]()
Данное дифференциальное уравнение, есть уравнение гармонических колебаний, и оно имеет решение вида:
7)
![]()
где j0 – угловая амплитуда колебаний; w - циклическая (круговая) частота; a - начальная фаза колебаний.
Круговая частота w и период колебаний T находятся через величины J и k по формулам:
8)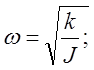
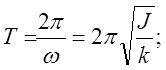
После снятия показаний с установки можно вычислить период колебаний:
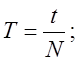 где t
– время колебаний; N
– число колебаний.
где t
– время колебаний; N
– число колебаний.
Время N полных колебаний системы можно найти так:
9)
![]() где
J0– момент инерции пустой рамки.
где
J0– момент инерции пустой рамки.
Затем измеряем t0 – время N полных колебаний ненагруженной рамки, tэ – время N полных колебаний рамки с грузом. Тело с известным моментом инерции называют эталонным телом.
Зависимость измеряемых времён от соответствующих моментов инерции задаётся системой уравнений:
10) 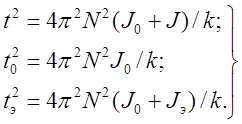
Исключив из этой системы неизвестные величины J0 и k получим формулу для неизвестного момента инерции тела (J):
11) ![]()
Из данного выражения следует формула для предельной относительной погрешности определяемого момента инерции:
|
|
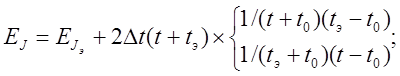
где ![]() - относительная погрешность момента
инерции эталонного тела; Dt –
погрешность измерения полного времени N колебаний
рамки (предположительно эта погрешность одинакова для всех трёх измерений: t0, t
и tэ).
- относительная погрешность момента
инерции эталонного тела; Dt –
погрешность измерения полного времени N колебаний
рамки (предположительно эта погрешность одинакова для всех трёх измерений: t0, t
и tэ).
Для упрощения расчётов формулу (11) можно преобразовать в следующее выражение:
13) 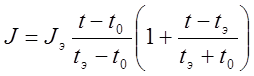 .
.
Вычисления моментов инерции тела можно производить и по формуле следующего вида:
14) 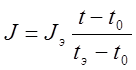 , но только при выполнении условия
приблизительного равенства значений времени t и tэ:
, но только при выполнении условия
приблизительного равенства значений времени t и tэ:
15) 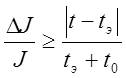 ;
;
Расчётная часть
|
№ опыта |
1 |
2 |
3 |
|
|
to, с |
12,661 |
12,660 |
12,663 |
12,661 |
|
t1, с |
15,172 |
15,197 |
15,221 |
15,197 |
|
t2, с |
18,060 |
18,049 |
18,070 |
18,060 |
|
tэ, с |
18,201 |
18,391 |
18,393 |
18,328 |
N = 20
После проведения опытов имеем значения следующих величин:
(Куб) …………… m1 = 0,950 кг. a= 36,6´10-3 м. (ребро куба).
(Параллелепипед) m2 = 1,850 кг. h= 100,3´10-3 м. b= 6´10-2 м. a= 4´10-2 м. (длина, ширина, высота).
(Цилиндр) ……… mэ = 1,708 кг. R= 31,5´10-3 м. h= 70,2´10-3 м. (радиус, высота)
Используя формулу (12) вычислим относительные погрешности моментов инерции для каждого тела. Для этого, по соответствующим формулам, найдём момент инерции эталонного тела (Jэ), абсолютную (DJэ) и относительную (EJэ) погрешности вычисления данной величины, а так же погрешность измерения полного времени N колебаний (Dt).
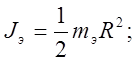
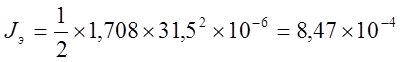 кг´м2.
кг´м2.
Вычислим DJэ по формуле нахождения абсолютной погрешности измерения косвенной величины.
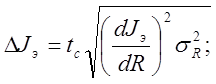 где
где 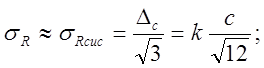 т. к. измерения радиуса эталонного
тела проводились штангенциркулем - с = 0,02 мм. = 2 ´ 10-5 м; k = 1,1.
т. к. измерения радиуса эталонного
тела проводились штангенциркулем - с = 0,02 мм. = 2 ´ 10-5 м; k = 1,1.
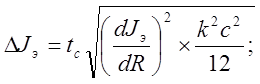
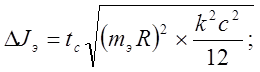
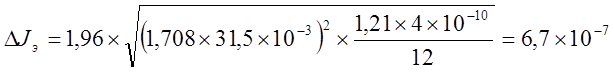 кг´м2.
кг´м2.
Найдём погрешность измерения полного времени N колебаний (Dt).
![]()
![]()
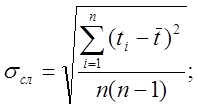
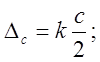
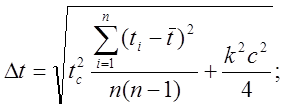
При n = 3, tс = 4,30; c = 10-3 с.
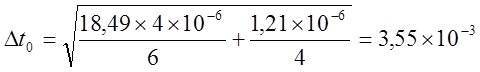 с.
с. 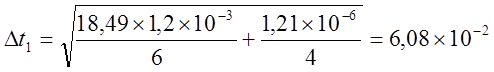 с.
с.
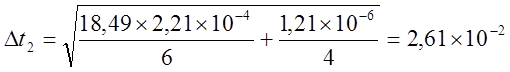 с.
с. 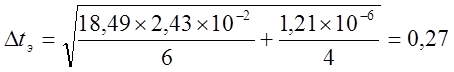 с.
с.
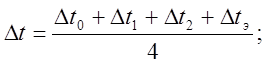
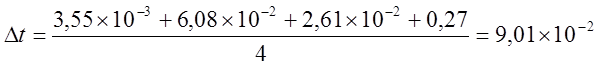 с.
с.
По следующей формуле подсчитаем относительную погрешность момента инерции эталонного тела.
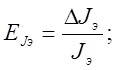
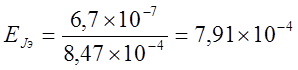
Для 1-ого тела найдём относительную погрешность
момента инерции. Будем использовать выражение (12) в следующем виде т. к. tэ > t1 (как значение t1 (и в дальнейших
вычислениях ti ) берётся значение ![]() (и
(и ![]() )):
)):
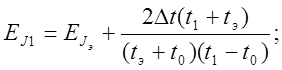
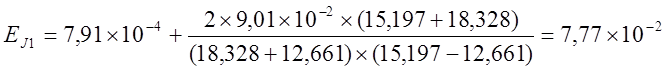
Относительная погрешность момента инерции для 2-ого тела:
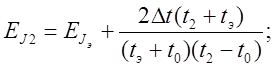
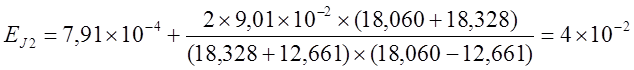
при tэ > t2.
Теперь, оценив соотношение (15), подсчитаем значение моментов инерции для 1-ого и 2-ого тел.
Для нахождения значения момента инерции 1-ого тела надо использовать формулу (13) т. к.
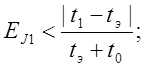
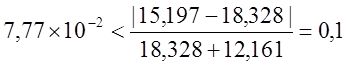
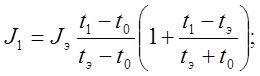
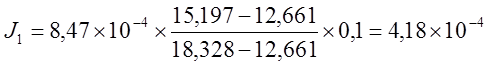 кг´м2.
кг´м2.
Для нахождения значения момента инерции 2-ого тела надо использовать формулу (15) т. к.
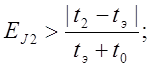
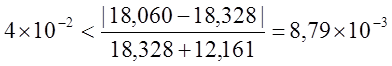
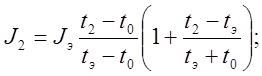
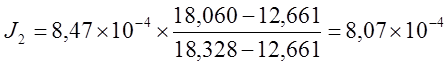 кг´м2.
кг´м2.
Далее, по формуле DJi = Ji ´ EJi, найдём погрешность для соответствующих моментов инерции тел.
DJ1 = J1 ´ EJ1; DJ1 = 4,18´10-4 ´ 7,77´10-2 = 3,25´10-5 кг´м2.
DJ2 = J2 ´ EJ2; DJ2 = 4´10-2 ´ 8,07´10-4 = 3,23´10-5 кг´м2.
Итого, практические значения моментов инерции данных тел таковы:
J1 = 41,8´10-5 ± 3,25´10-5 кг´м2.
J2 = 80,7´10-5 ± 3,23´10-5 кг´м2.
Найдём теоретические значения тех же величин.
Так, как оба исследуемых тела представляют собой параллелограммы, то их моменты инерции можно найти по следующим формулам:
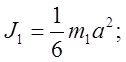
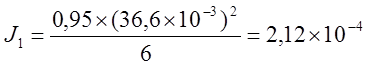 кг´м2. т.
к. 1-ое тело является кубом.
кг´м2. т.
к. 1-ое тело является кубом.
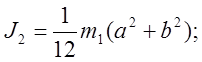
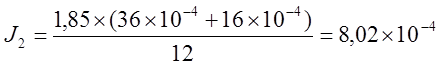 кг´м2. т.
к. стороны основания 1-ого тела не равны.
кг´м2. т.
к. стороны основания 1-ого тела не равны.
Вычислим абсолютные погрешности данных величин:
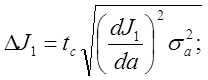 где
где 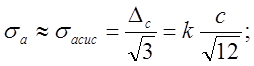 т. к. измерение стороны основания
данного тела проводилось штангенциркулем - с = 0,02 мм. = 2 ´ 10-5 м; k = 1,1.
т. к. измерение стороны основания
данного тела проводилось штангенциркулем - с = 0,02 мм. = 2 ´ 10-5 м; k = 1,1.
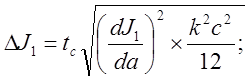
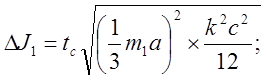
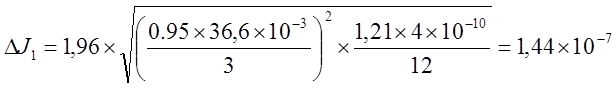 кг´м2.
кг´м2.
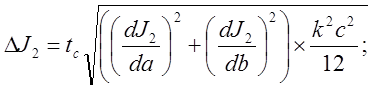
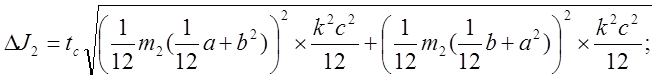 учитывая, что измерения сторон
основания данного тела проводились штангенциркулем.
учитывая, что измерения сторон
основания данного тела проводились штангенциркулем.
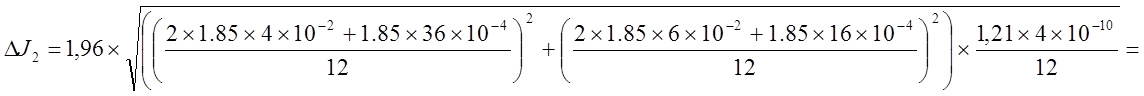 = 2,83´10-7 кг´м2.
= 2,83´10-7 кг´м2.
Выпишем, теоретические значения моментов инерции данных тел таковы:
J1 = 2,12´10-4 ± 0,00144´10-4 кг´м2.
J2 = 8,02´10-4 ± 0,00283´10-4 кг´м2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.