Методические указания к выполнению лабораторно-практических занятий по курсу «Математические модели и автоматизированные технологии», страница 3

Сравнить результаты расчета коэффициентов по уравнениям 5,6 и методом подстраиваемой модели, сделать  выводы.

Лабораторная работа №3

Пятый этап процесса построения модели заключается в проверке адекватности полученной модели. Проверку адекватности можно  осуществить так называемыми инженерными методами, которые позволяют только грубо оценить соответствие модели объекту. Сущность этих методов заключается в сравнении ошибки модели с наперед заданной ее величиной. Если ошибки модели по всем опытам не превышают ее заданное значение, то модель считается адекватной.

Наиболее точной и объективной является статистическая проверка адекватности модели. Статистическая проверка осуществляется в следующей последовательности:

1.  Проверка воспроизводимости опытов по критерию Кохрена.

Опыты считаются равноточными, если расчетный критерий Кохрена G_р меньше табличного G_т, то есть G_р<G_т. Значение табличного критерия G_т выбирается из статистических таблиц для уровня значимости  =0,05 при числе степеней свободы  и числе вариантов n (см. приложение Таблица 1). Расчетное значение критерия определяется по формуле 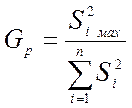7

                         ,                                                        (7)

где - построчные дисперсии воспроизводимости, вычисляемые по формуле 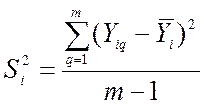8.

                                  ,                                               (8)

где как и выше, номер опыта в таблице наблюдений, q – номер повторения, m – количество повторений,  - среднее значение выходного параметра из двух повторений опытов, а - q – тый номер повторения опыта при том эксперименте. Числитель в формуле 7 – это максимальная из построчных дисперсий. В случае, если  G_р > G_т результатам данного эксперимента доверять нельзя и требуется проведение дополнительных повторений опытов или даже изменения набора входных параметров объекта.

При  G_р < G_т опытным данным можно доверять и можно производить дальнейшую статистическую проверку.

2.  Определение значимости коэффициентов модели.

При выполнении равноточности опытов определяется дисперсия эксперимента:

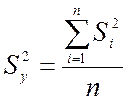                                                                                    (9)

Затем определяется доверительный интервал коэффициентов модели по формуле 10

                                   ,                                            (10)

где t – критерий Стьюдента, определяемый по статистическим таблицам  из условий уровня значимости  и числа степеней свободы  (см. приложение Таблица 2), а - среднеквадратическая ошибка коэффициентов математической модели, которая вычисляется по формуле:

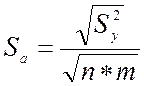                                                                                            (11)

В случае если  , коэффициент считается значимым, в противном случае коэффициент приравнивается к нулю и это слагаемое удаляется из структуры модели.

3.  Проверка адекватности  модели.

Модель считается адекватной, если расчетный критерий Фишера будет меньше или равен его табличному значению:

                                                                                          (12)

Табличный критерий определяется из статистических таблиц для уровня значимости  и числа степеней свободы  и  , где l – число значимых коэффициентов в модели (см. приложение Таблица 3).

Расчетный критерий Фишера определяется по формуле:

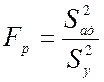                                     ,                                                     (13)

где  - дисперсия адекватности, определяемая по формуле:

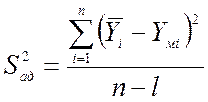                                                                                        (14)

Значение дисперсии опыта ранее рассчитывалось по уравнению  9. Остается оценить адекватность модели в соответствии с уравнением 12          и сделать выводы. В случае, если модель адекватна, то её можно использовать для решения практических задач (управление, оптимизация, прогнозирование и т.д.). Если модель не адекватна, то необходимо вернуться к третьему этапу моделирования – синтезу структуры модели, изменить структуру и проделать четвертый и пятый этапы вновь. В процессе построения модели таких этираций может быть несколько.

Лабораторная работа №4

Все выше изложенные лабораторные работы предполагают получение математической модели объекта в условиях активного спланированного эксперимента. Целью настоящей работы является получение математической модели в условиях пассивного эксперимента.

Пассивный эксперимент предполагает заполнение таблицы наблюдений  без вмешательства исследователя в ход нормальной эксплуатации объекта. Для реализации этого необходимо открыть программу «Объект 1» Лаб. работа №»21, в результате чего появится рабочее окно программы, приведенное на рисунке 7.

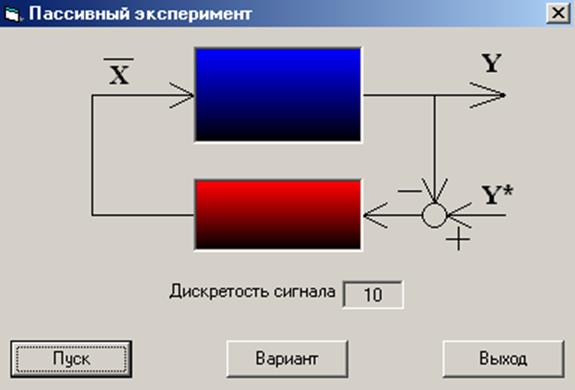
Рисунок 7 – Окно программы «Пассивный эксперимент»

Пассивный эксперимент проводится в следующем порядке:

1.  Устанавливается вариант объекта (тот же, что и был в активном эксперименте).

2.  Подготавливается таблица наблюдений (см. таблицу 2), в которой имеется n серий опытов (n задается преподавателем). Каждая серия опытов проводится при одном и том же значении Y_зад.