Информатика и выч. техника \ Математические модели и автоматизированные технологии

Методические указания к выполнению лабораторно-практических занятий по курсу «Математические модели и автоматизированные технологии», страница 2

Для реализации опытов на искусственном объекте необходимо:

1.  Запустить программу «Объект 1»;

2.  Из меню выбрать и запустить Лаб.11.exe, появится окно (рис.2);

3.  Установить номер варианта (по номеру ПК, рисунок 3);

Рисунок 3 -  Окно «Вариант»

4.  Установить значения факторов согласно выполняемому опыту;

5.  Через кнопку пуск запустить программу, появится окно «График» (Рисунок 4);

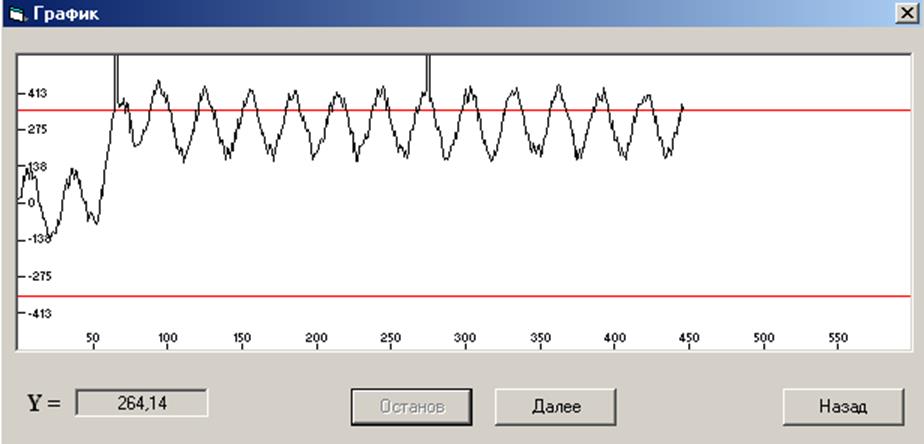Рисунок 4 - Окно «График»

6.  После разгона объекта, когда выходной параметр Y начнет колебаться возле некоторой постоянной величины, через кнопку «Останов», остановить программу и произвести запись значения Y1 в соответствующую строку таблицы наблюдений 1. Через кнопку «Далее» запустить и через несколько секунд вновь остановить программу, произвести запись значения Y2 в ту же строку таблицы наблюдений и через кнопку «Назад» вернуться к окну «Объект»(Рис. 2);

7.  Произвести изменения значений Х1 – Х4 согласно плана для следующего опыта и повторить пункты 5. 6 настоящего алгоритма;

8.  После заполнения всех 16 строк таблицы наблюдений произвести расчет построчных средних значений Yср.

Таблицу 1 целесообразнее всего реализовать в табличном процессоре Microsoft Excel, причем значения Y1 и Y2 можно копировать в окне «График», а затем вставлять в нужную ячейку Excel. В электронных таблицах Excel удобно осуществлять и дальнейшие расчеты, в том числе расчет Yср.

Лабораторная работа №2

Третий этап построения модели является одним из наиболее важных этапов. Выбор структуры математической модели осуществляется исследователем на основе сведений, полученных при выполнении второго этапа – сбора теоретической информации об объекте. Можно выбрать линейную модель, нелинейную с взаимодействиями факторов, нелинейную со степенными зависимостями, комбинацию перечисленных вариантов (как, например, в уравнении 1) или иную.

Четвертый этап – параметрическая идентификация объекта (настройка коэффициентов модели) может осуществляться бес поисковыми и поисковыми методами. К первым относится различные модификации метода наименьших квадратов, а ко вторым – метод подстраиваемой модели.

В случае ПФЭ, расчет коэффициентов по методу наименьших квадратов осуществляется по упрощенным формулам:

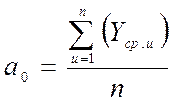,                                                                              (5)

где u – номер опыта (номер строки в матрице ПФЭ), а n – количество опытов.

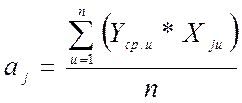,                                                                    (6)

где aj – коэффициент при j-том слагаемом уравнения 1,   Xju – значение j-того фактора в строке u (смотри таблицу 1).

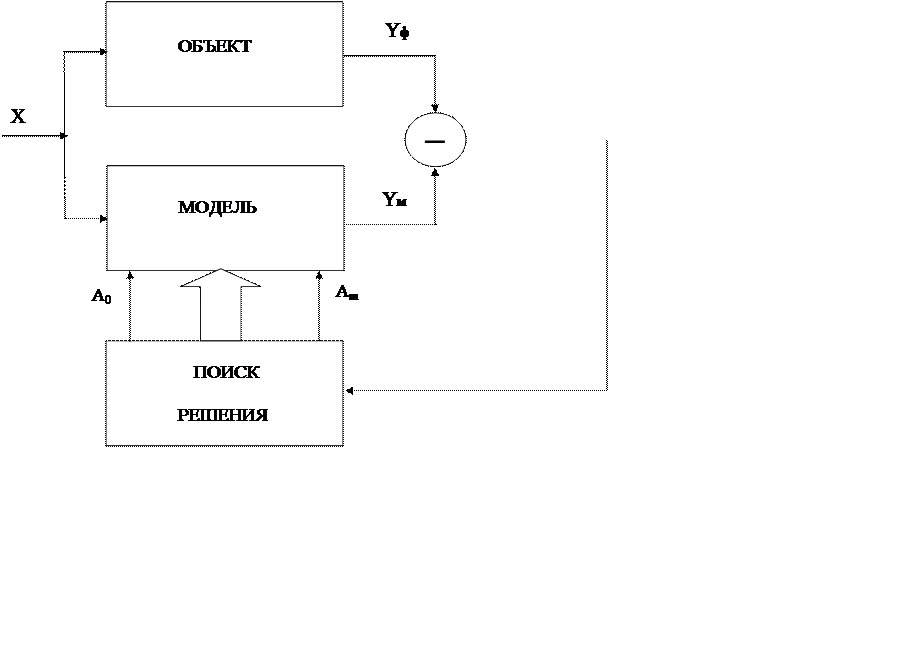
Возможности Microsoft Excel позволяют легко реализовать поисковый метод настройки коэффициентов модели. На рисунке 5 приведена схема подстраиваемой модели, использующая оптимизатор «Поиск решения» встроенный в MS Excel. Суть метода заключается в следующем. Сумма квадратов разностей по всем опытам между фактическим значением выходного параметра и модельным значением при одинаковых входных                                                                       

 


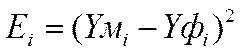
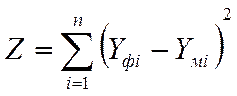
Рисунок 5 – Схема метода подстраиваемой модели    

параметрах минимизируется с помощью оптимизатора «Поиск решения» путем настройки  коэффициентов модели А0 – Аm.

Для выполнения лабораторной работы проведите расчет коэффициентов модели по формулам 5,6, затем реализуйте метод подстраиваемой модели и сравните полученные значения найденных коэффициентов.

Реализация метода подстраиваемой модели производится следующим образом:

1. На том же листе  MS Excel, на котором реализована таблица 1, формируется таблица коэффициентов модели, например, как таблица 2.

Таблица 2 – Таблица коэффициентов модели

A0

A1

A2

A3

A4

A5

A6

A7

A8

1

1

1

1

1

1

1

1

1

Следует отметить, что количество коэффициентов в таблице зависит от вида используемой для модели формулы, например, в формуле 1 имеется 15 коэффициентов. Для начала значения коэффициентов можно принять равными 1.

2. Используя возможности   MS Excel, рассчитать значения Yм для всех  16 опытов, для этого к таблице 1 добавить справа ещё один столбец.

3. Аналогично, добавив ещё один столбец, рассчитать построчные значения квадрата разности между фактическим значением выходного параметра Yср и модельным Yм – Ем.

4. Рассчитать сумму квадратов разностей по всем 16 опытам.

5. Открыть программу «Поиск решения», для чего войти в основное меню «Сервис», выбрать «Поиск решения» и нажать «ОК», откроется окно с инструментальной таблицей, приведенной на рисунке 6.

               

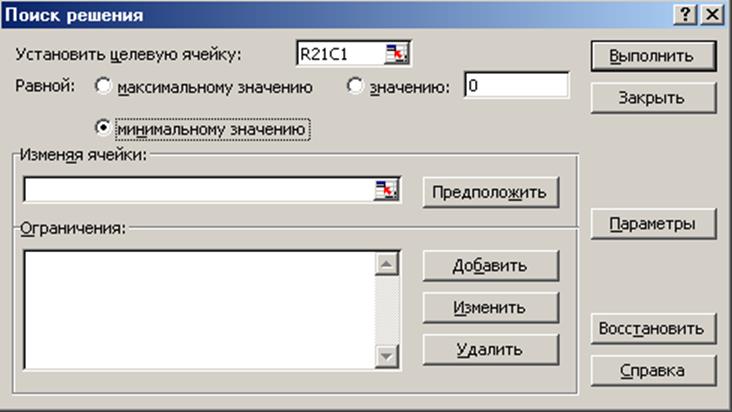
Рисунок 6 – Инструментальное окно оптимизатора «Поиск решения»

6. Установить целевую ячейку, в нашей задаче это ячейка, в которой хранится сумма квадратов разностей, для этого щёлкнуть на флажок окна «Установить целевую ячейку», а затем выделить ячейку с суммой квадратов разностей и, щёлкнув на флажок, выйти в таблицу «Поиск решения».

7. Установить, что целевая ячейка должна быть равна минимальному значению.

8. Щелкнуть на флажок в окне «Изменяя ячейки», пометить все ячейки значений коэффициентов модели (в нашем случае они равны 1) и через флажок вернуться в окно «Поиск решения».

9. Запустить программу «Поиск решения», нажав клавишу «Выполнить».

После выполнения программы в таблице коэффициентов выставятся расчетные значения этих коэффициентов.

Скачать файл