Енергетичний спектр і автокореляційна функція випадкового процесу

18

Енергетичний спектр і автокореляційна функція випадкового процесу є невипадковими функціями, пов'язаними між собою. Встановимо цей зв'язок.

Розглянемо реалізацію S (t) випадкового процесу від його зсунутій у часі копії S (t - τ).

З цією метою застосовується поняття АКФ. АКФ сигналу визначають, як скалярний добуток сигналу та його зсунутої в часі копії:

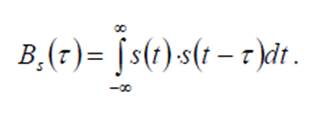
Формула Релея дозволяє розрахувати скалярний добуток, застосовуючи спектральні функції сигналів.

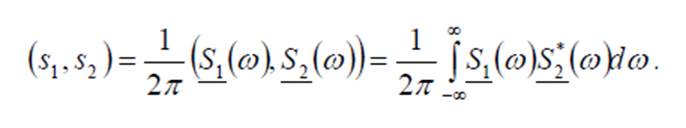
Підінтегральна функція в формулі Релея являє собою взаємний енергетичний спектр двох дійсних сигналів.

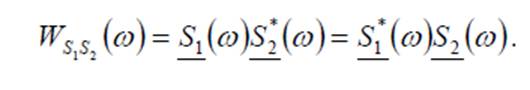
Враховуючи це, можна побачити, що скалярний добуток двох дійсних сигналів можна розрахувати як інтеграл від їх взаємного енергетичного спектру.

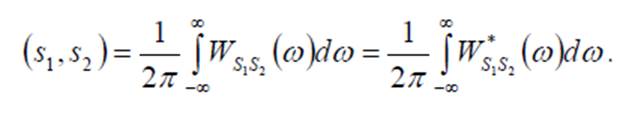
Зрозуміло, що у випадку дійсних сигналів, дійсні частини функції спектральної густини електричних сигналів це парні функції, а уявні – функції непарні, тому скалярний добуток сигналу можна вважати функцією тільки дійсної частини взаємної енергії спектру.

Легко показати, що існує зв’язок між АКФ та енергетичним спектром сигналу. Для цього треба використати узагальнену формулу Релея:

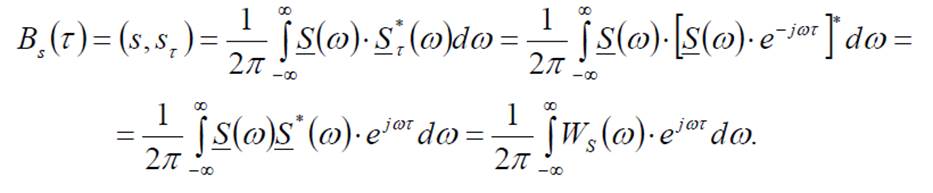
Отриманий вираз показує, що АКФ сигналу пов’язана з його енергетичним спектром за співвідношенням зворотного перетворення Фур’є. В свою чергу енергетичний спектр сигналу можна розраховувати шляхом застосування прямого перетворення Фур’є до АКФ сигналу:

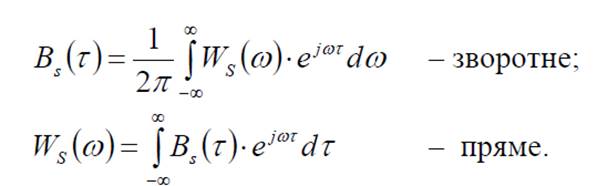
Так как автокорреляционная функция  и энергетический спектр являются вещественными четными функциями, можно отказаться от комплексной формы записи преобразования Фурье и перейти к другой форме.

,   

. 

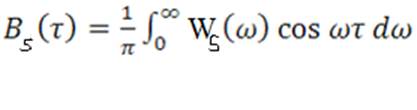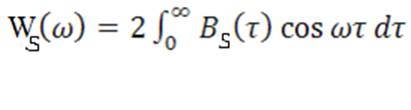Теорема Вінера-Хінчина відкриває можливість у відповідній формі перенести методи спектрального аналізу детермінованих сигналів і лінійних кіл на випадкові сигнали.