Взаимное преобразование критериев подобия

ЛЕКЦИЯ 9

Взаимное преобразование критериев подобия

         Некоторые из полученных критериев не всегда удобны в применении, ибо комплекты составлены из величин, измерение которых в опыте не всегда возможно. Например, при исследовании движений, обусловленных разностью плотностей отдельных элементов жидкости, измерить скорость их перемещений практически невозможно. В этом случае вместо критерия Фруда удобнее использовать критерий Галилея – .

.

; .

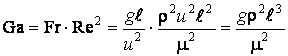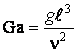Умножим критерий Галилея на симплекс , где   и  – плотность жидкости в двух соседних точках, получим критерий Архимеда – .

.

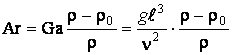В случае, когда разность плотностей обусловлена разностью температуры , то симплекс , где  – коэффициент объемного расширения жидкости. Подставим это выражение в критерий Архимеда и получим критерий Грасгофа – .

.

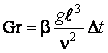Критерий Эйлера обычно используют также в несколько видоизмененном виде. Вместо давления применяется разность давлений в двух точках

.

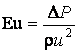Тепловое подобие

         В подавляющем большинстве случаев течение жидкости сопровождается теплообменом. Поэтому, чтобы подобие явления было более полным, необходимо кроме геометрического и механического подобия установить факт наличия теплового подобия. Это означает подобие температурных полей и тепловых потоков. Будем считать физические свойства жидкости (кроме плотности) постоянными. Зависимость плотности от температуры учитывается в механическом подобии при определении члена уравнения движения, выражающего Архимедову силу.

         С достаточной точностью эту зависимость можно считать линейной

,

где  – плотность при температуре ;  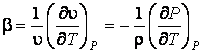– температурный коэффициент объемного расширения.

         В других членах уравнения движения и уравнениях энергии и неразрывности плотность будем считать постоянной. Пренебрегая диссипативной функцией, при отсутствии внутренних источников тепловыделений с учетом вышеотмеченных предположений уравнение энергии может быть записано в виде

.

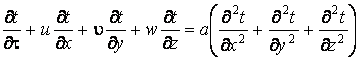Необходимо воспользоваться еще уравнением теплообмена

.

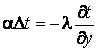Запишем эти уравнения для двух подобных систем

         На основании подобия процессов запишем:

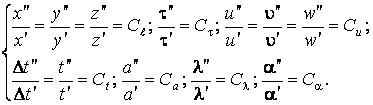
Заменим переменные второй системы через переменные первой и константы подобия, получим

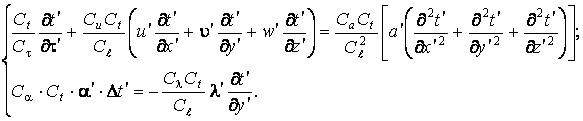
Из условия тождественности уравнений для первого и второго процессов получим следующие соотношения.