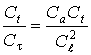Взаимное преобразование критериев подобия, страница 2

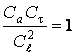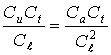 или ;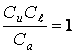

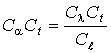 или ;

 или .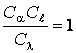

Заменим константы подобия отношениями величин

;  – критерий Пекле.

;  – критерий Фурье.

;  – критерий Нуссельта.

Таким образом, при тепловом подобии между собой двух или нескольких физических явлений (тепловых) для любых сходственных точек критерии подобия  имеют одни и те же численные значения. Критерий Пекле можно представить в виде произведения двух критериев, а именно

,

где  – критерий Прандтля. Он состоит лишь из физических параметров, характеризующих свойства жидкости.

.

Для газов одинаковой атомности критерий  является постоянной величиной, не зависящей ни от давления, ни от температуры. Для одноатомных газов ; двухатомных – ; трехатомных – ; четырехатомных и более .

         При изучении теплообмена обычно искомой величиной является коэффициент теплоотдачи . Поэтому критериальные уравнения конвективного теплообмена обычно имеют вид

.

Так как обязательной предпосылкой теплового подобия является механическое, то в качестве аргументов в критериальные уравнения должны войти критерии  и .

,

.

Физический смысл критериев подобия теплообмена

         Наличие гидродинамического подобия однозначно определяет численную одинаковость критериев подобия  или , которые принято называть критериями гидродинамического подобия. , , ,  – все эти критерии называются критериями теплового подобия. Каждый критерий несет вполне определенную смысловую физическую информацию. Критерий

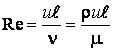
можно охарактеризовать как отношение инерциальных сил к силам вязкости. Действительно, силы вязкости пропорциональны кинематической или динамической вязкости, в то время как гиперциальные силы пропорциональны массе и скорости, то есть величинам, составляющим числитель отношения –

, .