Выполнил |
|
Студент |
Попов И. О. |
|
Группа |
А – 01 – 03 |
|
Вариант |
1 |
|
Дата |
03.10.07 |
Принял |
|
Преподаватель |
Шихин В.А. |
Дата |
Задача 010101
Решить геометрически и симплекс-методом:
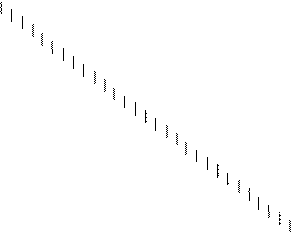
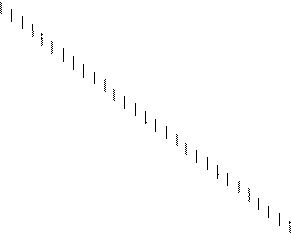
Решение геометрически.
Для решения поставленной задачи
геометрически необходимо в плоскости ![]() изобразить
область допустимых значений (D), границы которой будут
определяться выражениями:
изобразить
область допустимых значений (D), границы которой будут
определяться выражениями:
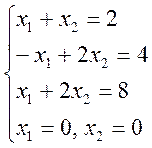
|
![]()
![]()
![]()
![]()
![]()









|
|
|

|
|
|
|
|
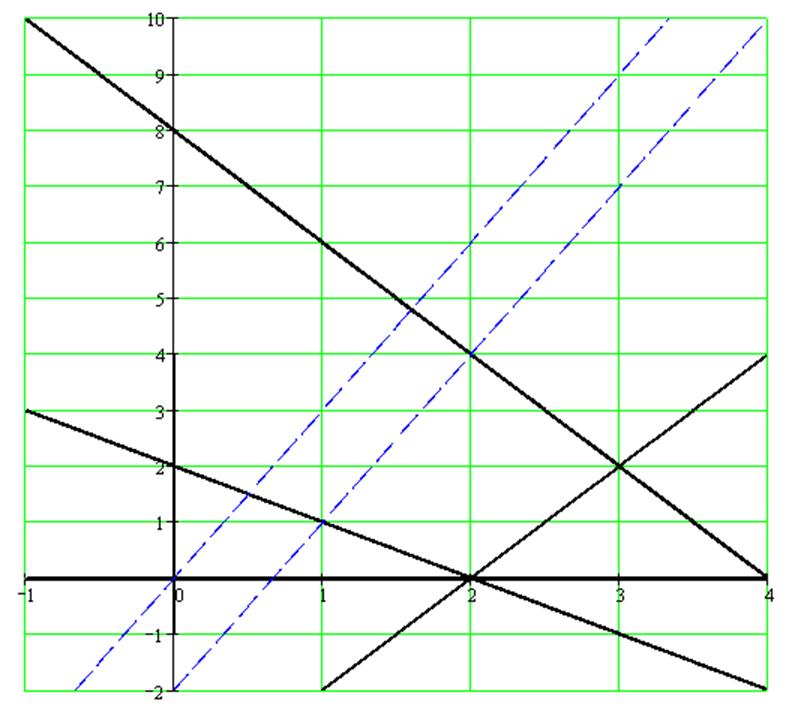
Т.к. D является непустым ограниченным замкнутым множеством, то задача имеет решение, причем точка оптимума расположена в одной из вершин D.
Т.к. различным
значениям целевой функции y на
плоскости ![]() соответствуют параллельные прямые,
то для определения направления возрастания целевой функции необходимо в
плоскости
соответствуют параллельные прямые,
то для определения направления возрастания целевой функции необходимо в
плоскости ![]() изобразить 2 произвольные из них:
изобразить 2 произвольные из них:
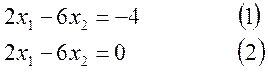
Т.о. целевая функция будет возрастать в направлении от прямой (1) к прямой (2), и достигнет оптимума в точке, в которой обращаются в равенства следующие 2 ограничения:
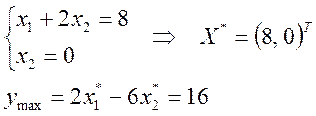
Ответ: ![]() ;
; ![]() .
.
Решение симплекс методом.
шаг 0.
Для применения
симплекс-метода задача линейного программирования должна быть сведена к
канонической задаче линейного программирования. С этой целью необходимо ввести
дополнительные переменные ![]() :
:
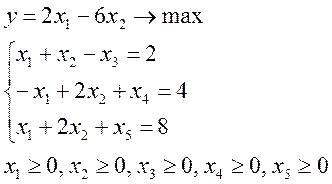
Для нахождения
первоначального базисного решения все переменные разбиваются на основные и
неосновные. Т.к. каждая из основных переменных должна входить только в одно
уравнение из системы ограничений, то кандидатами в основные являются переменные
![]() . Для проверки правильности выбора
необходимо проверить матрицу из коэффициентов при кандидатах на вырожденность:
. Для проверки правильности выбора
необходимо проверить матрицу из коэффициентов при кандидатах на вырожденность:
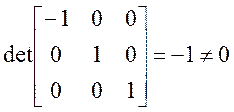 , следовательно выбор верен.
, следовательно выбор верен.
шаг 1.
основные переменные: ![]()
неосновные переменные: ![]()
При выражении основных переменных через неосновные система ограничений переписывается в виде:
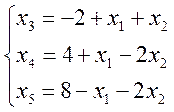
Если
приравнять неосновные переменные к 0, то получается базисное решение ![]() ,
являющееся недопустимым, т.к. не выполнено условие неотрицательности
,
являющееся недопустимым, т.к. не выполнено условие неотрицательности ![]() .
.
Для
получения допустимого базисного решения необходимо увеличить ![]() за счет увеличения
за счет увеличения ![]() . Следовательно
. Следовательно ![]() переводится в основные переменные при
условии исполнения ограничений на неотрицательность переменных:
переводится в основные переменные при
условии исполнения ограничений на неотрицательность переменных:
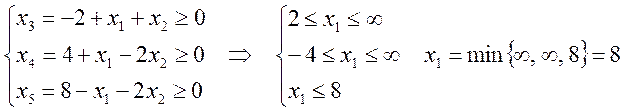
Третье
ограничение будет являться разрешающим, следовательно ![]() переводится
в неосновные переменные. Система
переписывается в виде:
переводится
в неосновные переменные. Система
переписывается в виде:
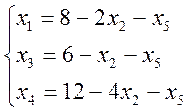
Приравнивая
неосновные переменные к 0, можно получить базисное решение ![]() ,
которое будет являться допустимым.
,
которое будет являться допустимым.
Проверка полученного решения на оптимальность дает следующие результаты:
![]()
Из выражения для целевой функции видно, что дальнейшее увеличение не допускается, следовательно достигнут оптимум:
![]()
Ответ:
![]() ;
; ![]() .
.
Задача 010201
Решить симплекс-методом:
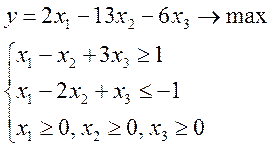
шаг 0.
Для применения
симплекс-метода задача линейного программирования должна быть сведена к
канонической задаче линейного программирования. С этой целью необходимо ввести
дополнительные переменные ![]() :
:
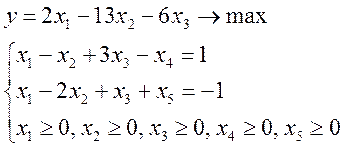
Для нахождения
первоначального базисного решения все переменные разбиваются на основные и
неосновные. Т.к. каждая из основных переменных должна входить только в одно
уравнение из системы ограничений, то кандидатами в основные являются переменные
![]() . Для проверки правильности выбора
необходимо проверить матрицу из коэффициентов при кандидатах на вырожденность:
. Для проверки правильности выбора
необходимо проверить матрицу из коэффициентов при кандидатах на вырожденность:
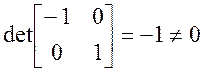 , следовательно выбор верен.
, следовательно выбор верен.
шаг 1.
основные переменные: ![]()
неосновные переменные: ![]()
При выражении основных переменных через неосновные система ограничений переписывается в виде:
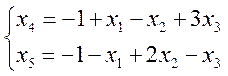
Если
приравнять неосновные переменные к 0, то получается базисное решение ![]() , являющееся недопустимым, т.к. не
выполнены условия неотрицательности
, являющееся недопустимым, т.к. не
выполнены условия неотрицательности ![]() и
и ![]() .
.
Для
получения допустимого базисного решения необходимо увеличить ![]() за
счет увеличения
за
счет увеличения ![]() . Следовательно
. Следовательно ![]() необходимо перевести в основные переменные
при условии исполнения ограничений на неотрицательность переменных:
необходимо перевести в основные переменные
при условии исполнения ограничений на неотрицательность переменных:
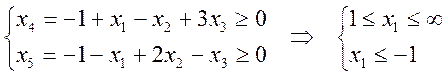
Т.к. ограничения на неотрицательность переменных не
выполняются, то такая операция недопустима. Аналогично ![]() может
быть увеличено за счет увеличения
может
быть увеличено за счет увеличения ![]() :
:
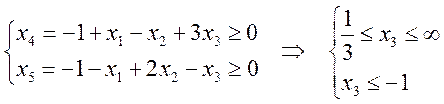
Т.к.
ограничения на неотрицательность переменных не выполняются, то такая операция
недопустима. Аналогично ![]() может быть
увеличено за счет увеличения
может быть
увеличено за счет увеличения ![]() :
:
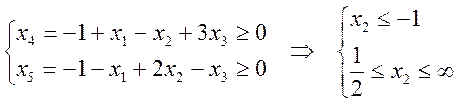
Т.к. ограничения на неотрицательность переменных не выполняются, то такая операция недопустима.
Т.к
улучшить первоначальное недопустимое базисное решение ![]() не
удается, то необходимо вернуться на шаг 0 с целью выбора других основных
переменных.
не
удается, то необходимо вернуться на шаг 0 с целью выбора других основных
переменных.
шаг 0.
Для осуществления этой операции необходимо исключить
из первого уравнения ![]() , а из второго
, а из второго ![]() :
:

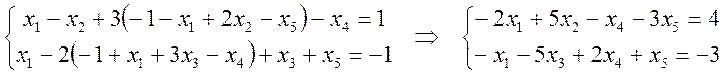
Т.о.
кандидатами в основные являются переменные ![]() .
Для проверки правильности выбора необходимо проверить матрицу из коэффициентов
при кандидатах на вырожденность:
.
Для проверки правильности выбора необходимо проверить матрицу из коэффициентов
при кандидатах на вырожденность:
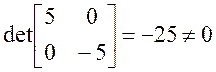 , следовательно выбор верен.
, следовательно выбор верен.
шаг 1.
основные переменные: ![]()
неосновные переменные: ![]()
При выражении основных переменных через неосновные система ограничений переписывается в виде:
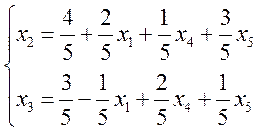
Приравнивая
неосновные переменные к 0, можно получить базисное решение 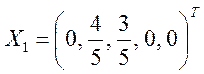 , которое будет являться допустимым.
, которое будет являться допустимым.
Проверка полученного решения на оптимальность дает следующие результаты:
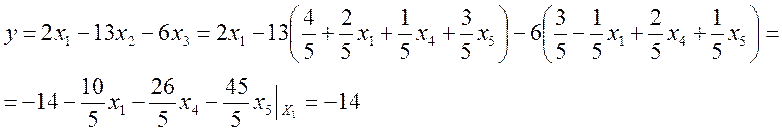
Из выражения для целевой функции видно, что дальнейшее увеличение не допускается, следовательно достигнут оптимум:
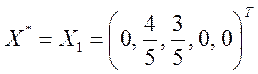
Ответ: 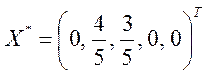 ;
; ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.