Первичный анализ временного ряда и вторичный анализ стохастической составляющей исследуемого сигнала, страница 6

 АР(55) =  -0.03269386117   0.02117916217    1.543680572      0.06138662473   

 АР(56) =  -0.05102210066   0.01928667184    2.645459055      0.004100703447  

 АР(57) =  -0.03740694192   0.0182446405     2.050297562      0.02021190434   

           Сумма кв. Остатков =7.475575061     

          Хи-Квадрат Тест автокорреляции Остатков =190.6378216     

             с числом степеней свободы = 1               

          Остатки есть Белый Шум с вероятностью не более чем =0               

_________________________________________________________________________________

_________________________________________________________________________________

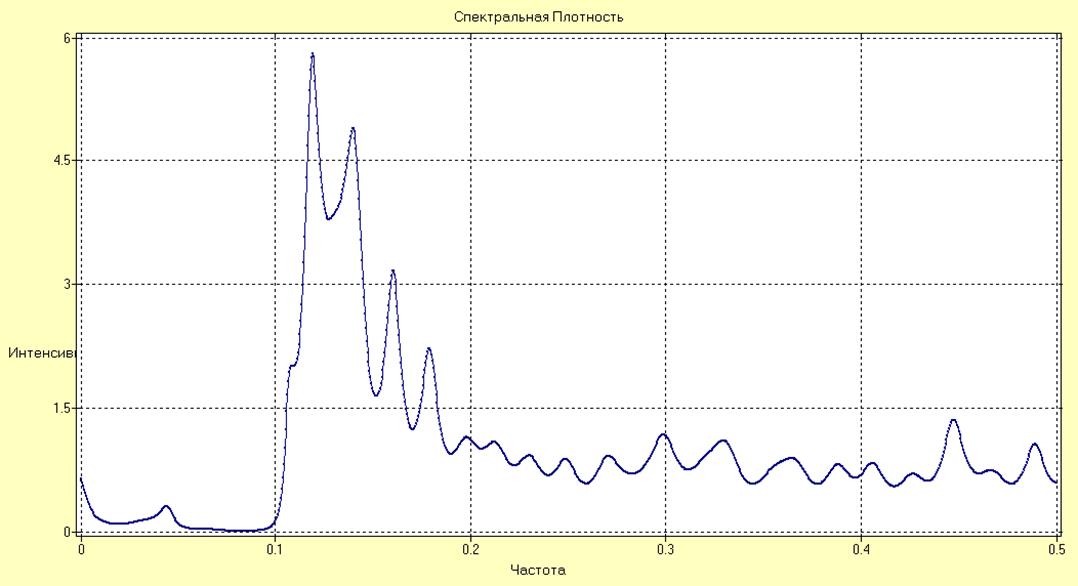
Рис.26. СПМ для параметрический АР модели (Левинсона-Дурбина).

5%

-5%

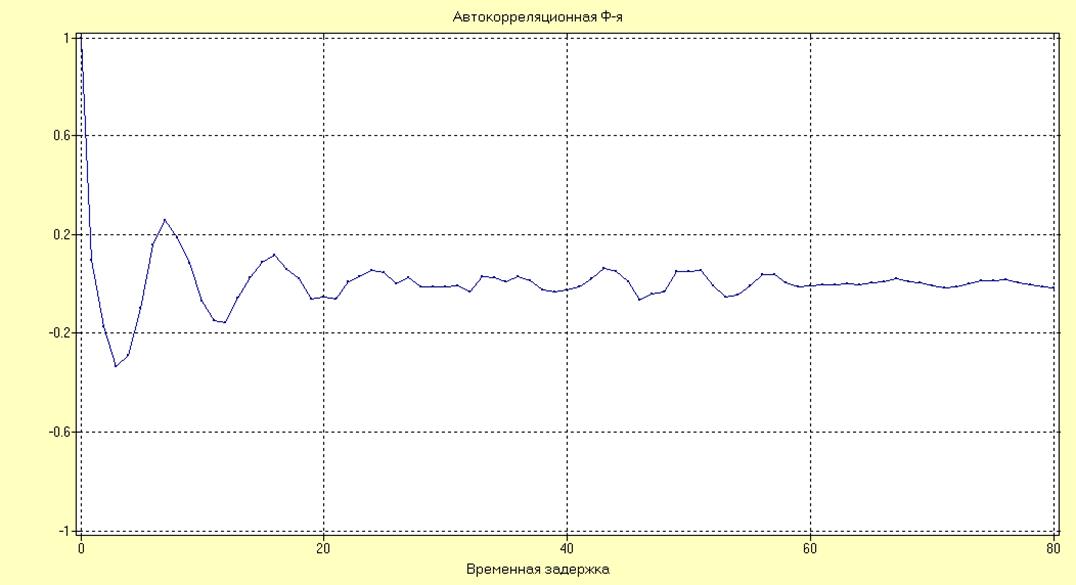Рис. 27. Автокорреляционная функция для параметрический АР модели (Левинсона-Дурбина).

____________________________________________________________________________

     Переменная d:\tr\o_h_w.filtrout0

          Параметры АРСС Модели

  Параметр  Оценка          Станд.Ошибка     T-Значение       P-Значение

 АР(1) =   0.125112448      0.04769766182    2.623031052      0.004483985418  

 СС(1) =   -0.09620702131   0.04083871445    2.355779867      0.009424958321  

 СС(2) =   -0.3539141872    0.02096598196    16.88040121      0               

 СС(3) =   -0.2529092151    0.02212220015    11.43237171      4.440892099e-16 

 СС(4) =   -0.3530896067    0.01807275493    19.53712138      1.110223025e-16 

 СС(5) =   -0.1034139953    0.02046936375    5.052135307      3.018276272e-07 

 СС(6) =   0.1358948702     0.01852369376    7.336272772      4.18443058e-13  

 СС(7) =   0.140329171      0.02013461823    6.969547145      4.778955009e-12 

 СС(8) =   0.1544299599     0.01878760555    8.219778698      6.661338148e-16 

 СС(9) =   0.227079699      0.01751666033    12.96364117      0               

 СС(10) =  0.1173422817     0.01712273327    6.853011131      1.01492148e-11  

 СС(11) =  0.03669796941    0.01694727914    2.16541954       0.01540217767   

 СС(12) =  -0.06619986719   0.01633470802    4.052711998      2.913697323e-05 

 СС(13) =  -0.09553035162   0.0145014797     6.587627854      5.430289551e-11 

 СС(14) =  -0.1080541267    0.004409439651   24.50518325      0               

 СС(15) =  -0.152060017     0.01537416088    9.890622211      0               

 СС(16) =  -0.08210568694   0.01700820375    4.827416706      9.078092527e-07 

 СС(17) =  0.01589981665    0.01745287422    0.9110142233     0.1813525878    

 СС(18) =  0.107329728      0.01700361882    6.312169726      2.925805154e-10 

 СС(19) =  0.1338150213     0.01723754363    7.762998267      2.142730438e-14 

 СС(20) =  0.2625332656     0.01634174787    16.06518885      2.220446049e-16 

          Константа =-0.00119060117  

          Дисперсия Остатков =0.003804260312  

           Сумма кв. Остатков =11.33289147     

          Хи-Квадрат Тест автокорреляции Остатков =1354.992455     

             с числом степеней свободы = 526             

          Остатки есть Белый Шум с вероятностью не более чем =0               

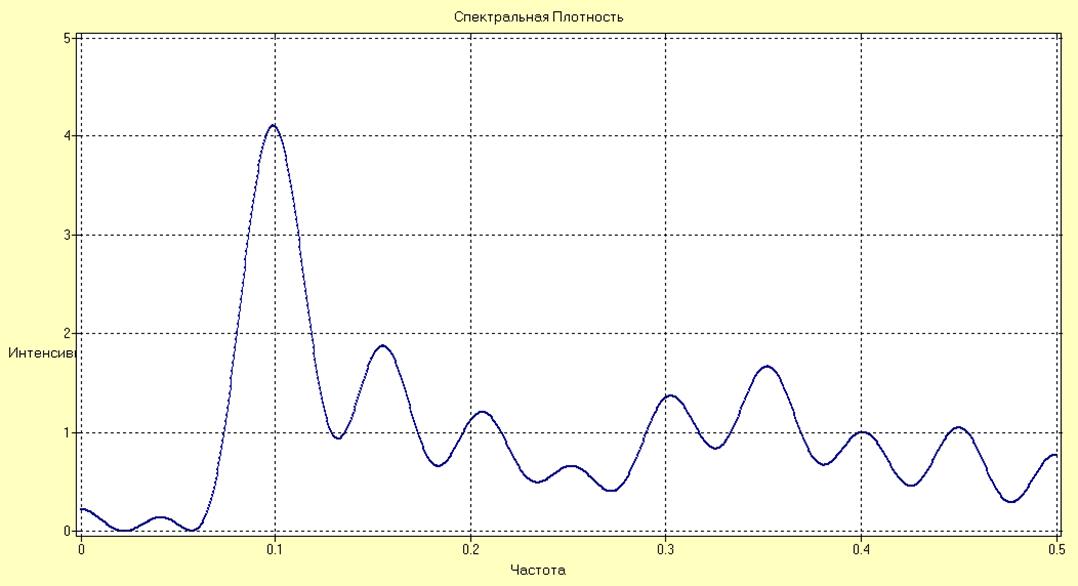
Рис.28. Спектральная плотность для параметрической АРCC модели.

5%

-5%

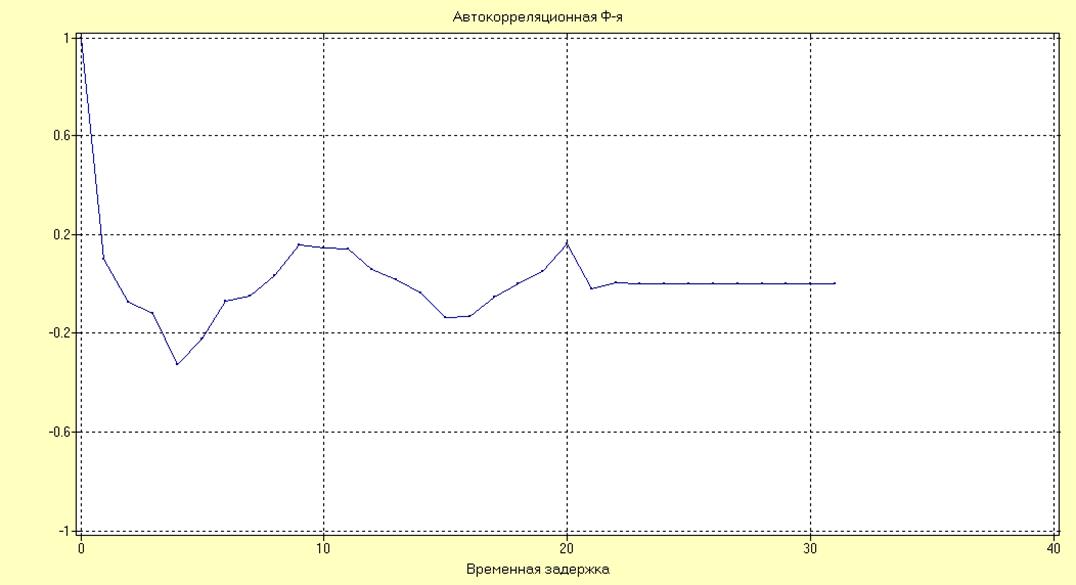
Рис.29. Автокорреляционная функция для параметрической АРCC модели.

Исходя из результатов приближения ряда АР и АРСС моделью, можно сделать вывод, что в нашем случае применение АР модели по методу Берга предпочтительнее, так как сумма среднеквадратичной ошибки в этом случае минимальна.

Конечный процесс АР(p) имеет бесконечно протяженную автокорреляционную функцию и финитную частную корреляционную функцию, а процесс CC(p) имеет бесконечно протяженную частную корреляционную функцию и автокорреляционную функцию, обращающуюся в нуль после некоторой точки. Т.е. для параметрического оценивания АР(p) процесса следует использовать частную автокорреляционную функцию, а для СС(p) процесса –  просто автокорреляционную функцию.

Расчет частной автокорреляционной функции модели.

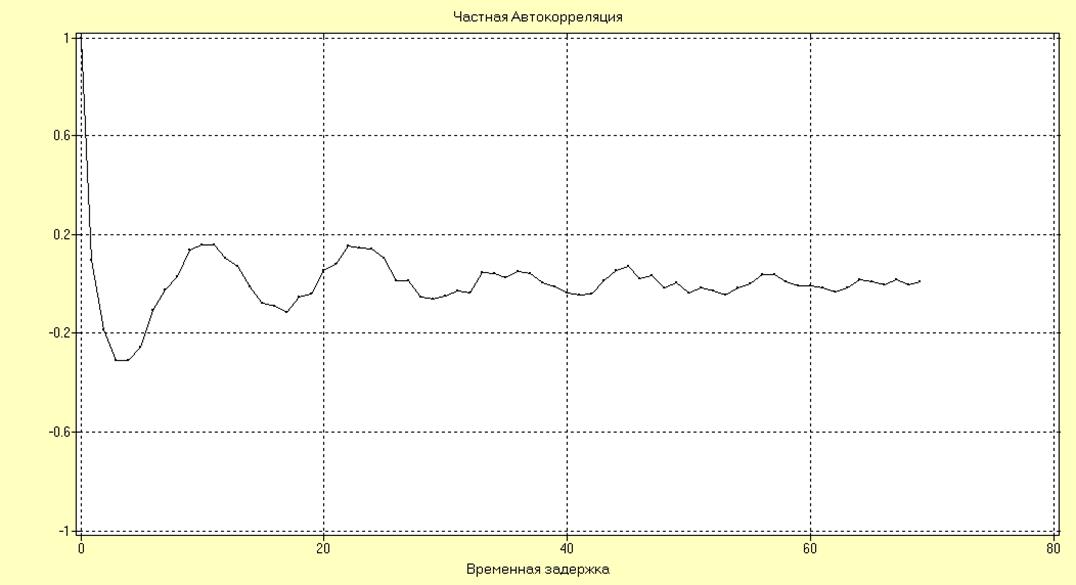
Рис. 17. Частная корреляционная функция.

По виду частной корреляции можно сделать вывод, что порядок модели – 57.

1.6 Выводы

     Сравнение СПМ для параметрического и непараметрического методов показывают, что наибольшее распределение мощности наблюдается на средних частотах. В меньшей степени – на высоких частотах. Мощность на низких частотах незначительная. При непараметрическом методе оценивания СПМ наблюдаются следующие характерные частоты: 0.125, 0.15, 0.17, 0.185, 0.445. Для параметрических методов оценивания методами Берга и Левинсона-Дурбина наибольшие всплески мощности на частотах:  0.125, 0.133, 0.166, 0.185, 0.45. Следовательно, можно сделать вывод о близости полученных оценок СПМ.  

Параметрические оценки, полученные с помощью блочных алгоритмов, состоятельны и имеют нормальное распределение. При сравнении свойств оценок следует отметить, что непараметрическая оценка СПМ в виде простой периодограммы обладает наибольшей разрешающей способностью, хотя и является статистически неустойчивой оценкой.

Сравнение АКФ параметрического и непараметрического методов показывают, что наблюдаются следующие значения интервалов максимальной корреляции: для непараметрического оценивания – 11 отсчетов; для параметрических – 17 (метод Левинсона-Дурбина), 22 (АРСС модель), 22 (метод Берга).

     Исходный ряд содержал монотонно убывающий тренд и колебательные составляющие на низких частотах. Характерными частотами являлись: 0,003 и 0,0067. Максимальный интервал корреляции 66. Так как исходный ряд был нестационарным по мат. ожиданию, то из него был обнаружен и удален монотонный тренд, после чего ряд вновь оказался нестационарным. Поэтому было проведено удаление колебательных составляющих, после чего был получен стационарный ряд по мат. ожиданию и дисперсии.