Первичный анализ временного ряда и вторичный анализ стохастической составляющей исследуемого сигнала, страница 3

Рис. 11. Третья колебательная составляющая.

Произведем удаление всех найденных колебательных составляющих из временного ряда с помощью полосно-заграждающего фильтра.

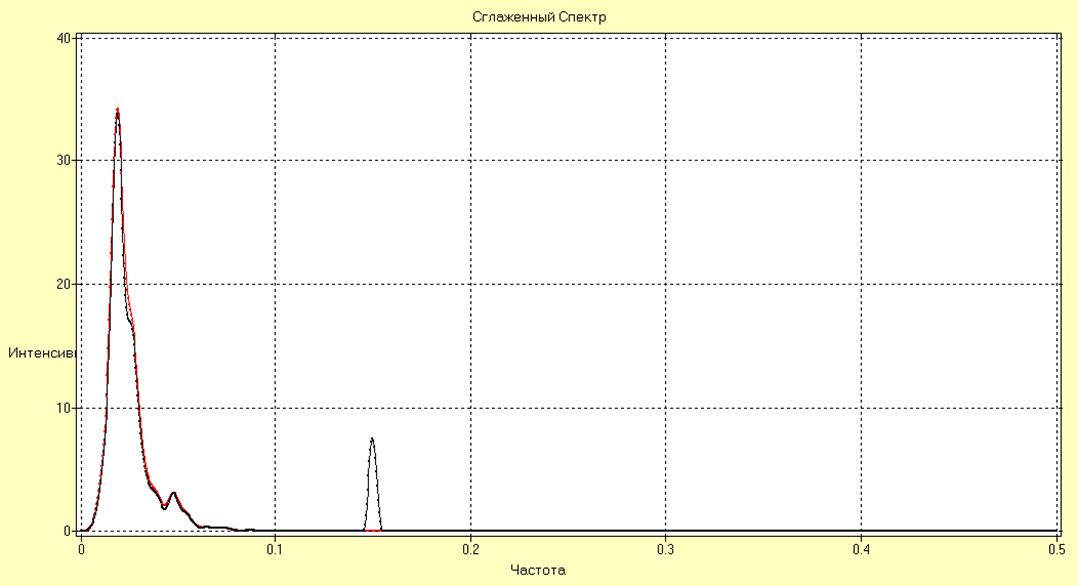
Рис. 12. Спектр исходного ряда и ряда с удаленной 3 гармоникой.

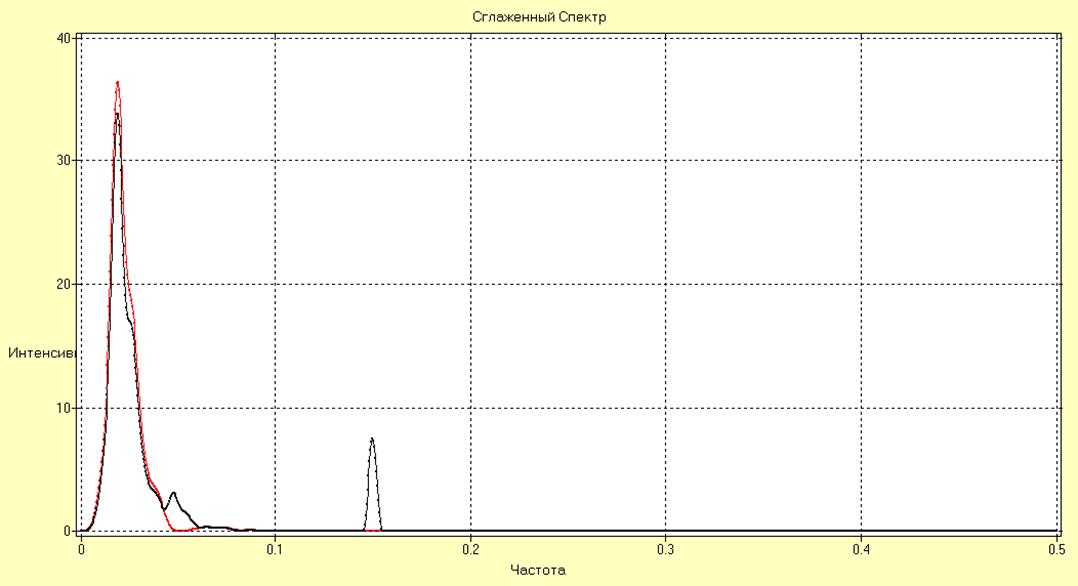
Рис. 13. Спектр исходного ряда и ряда с удаленными 2 и 3 гармониками.

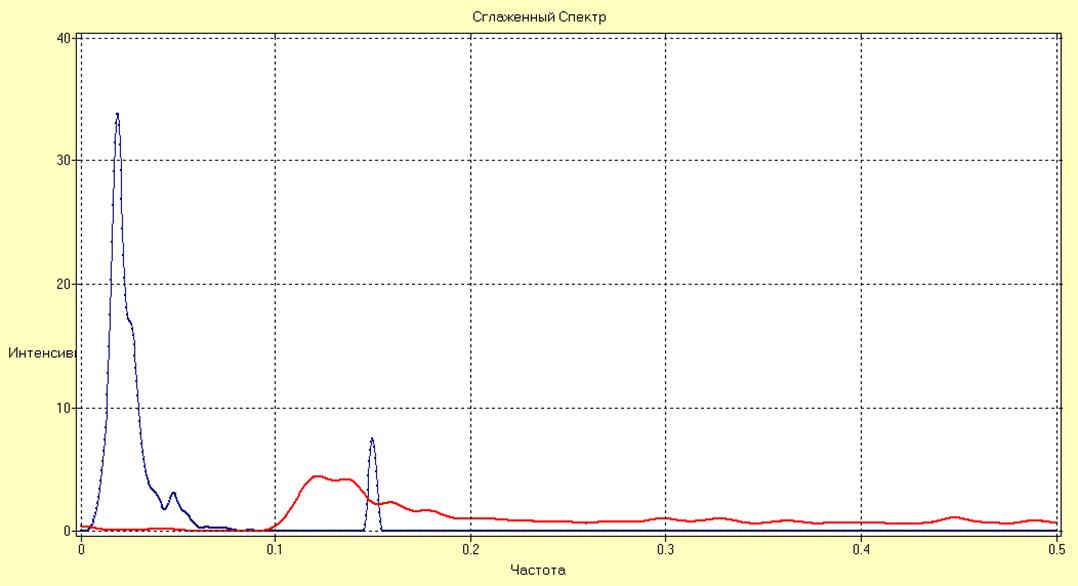
Рис. 14. Последовательное удаление всех гармонических составляющих из ряда.

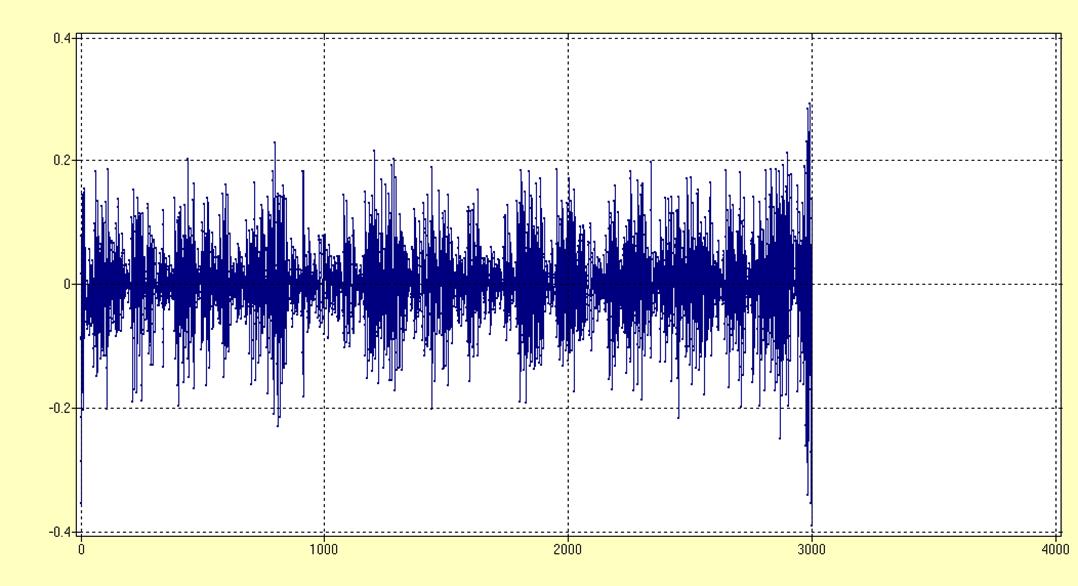
Рис.15. Временной ряд, полученный после фильтрации.

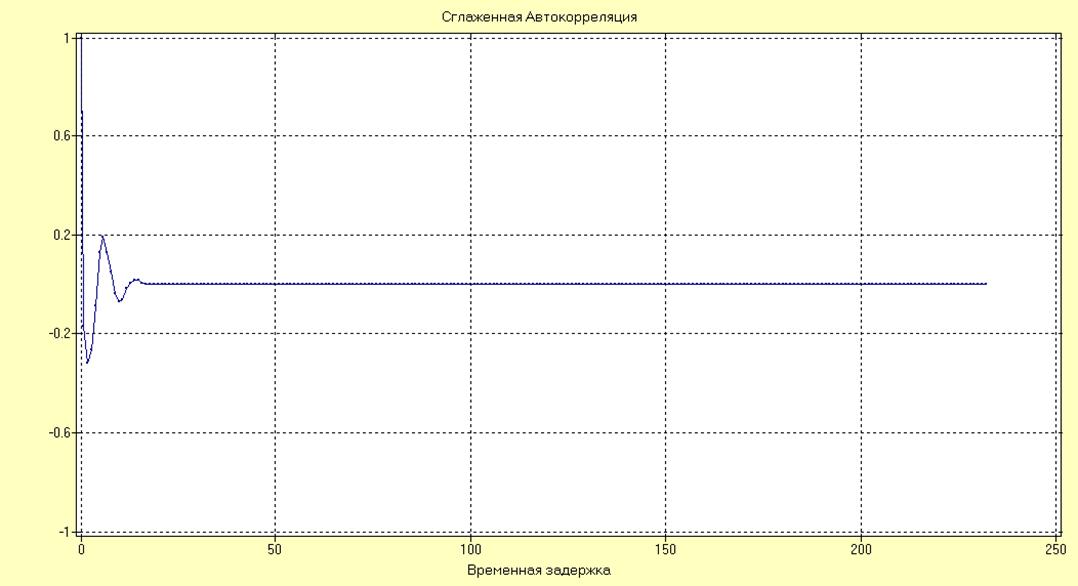
Рис.16. Сглаженная автокорреляционная функция ряда после фильтрации.

1.5 Выделение фрагмента ряда после удаления тренда и колебательных составляющих в виде стационарной случайной компоненты

Проведем повторное исследование ряда на стационарность в смысле стационарности по мат ожиданию и дисперсии.  Для этого разобьем ряд на равные по времени интервалы, и посчитаем математическое ожидание и дисперсию в каждом из этих интервалах отдельно. Результаты расчетов представлены ниже:

                                                                    Основные Статистики

                  o_h_w.z1        o_h_w.z10       o_h_w.z11       o_h_w.z2       

Среднее значение  -0.01018383105  0.000463853016  -0.0002643575179-0.0006906417494

Дисперсия         0.006978976899  0.005537845934  0.004923375663  0.004087278743 

                  o_h_w.z12       o_h_w.z3        o_h_w.z4        o_h_w.z5       

Среднее значение  -0.002965189104 0.0004628312195 0.0001898839523 0.0001800223746

Дисперсия         0.0124928168    0.003478189711  0.004571424463  0.00374399817  

                  o_h_w.z6        o_h_w.z7        o_h_w.z8        o_h_w.z9       

Среднее значение  -0.00057251952680.0007681787916 -0.00011013081650.0001578575176

Дисперсия         0.005060119775  0.002635368666  0.005542098239  0.004478910201

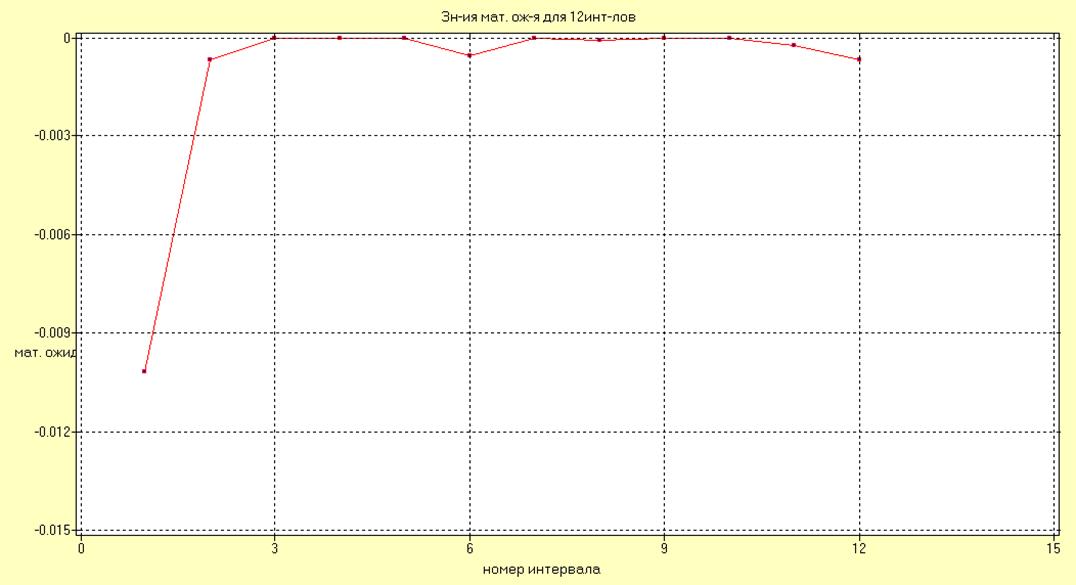
Рис.17. Значения математических ожиданий для всех интервалов

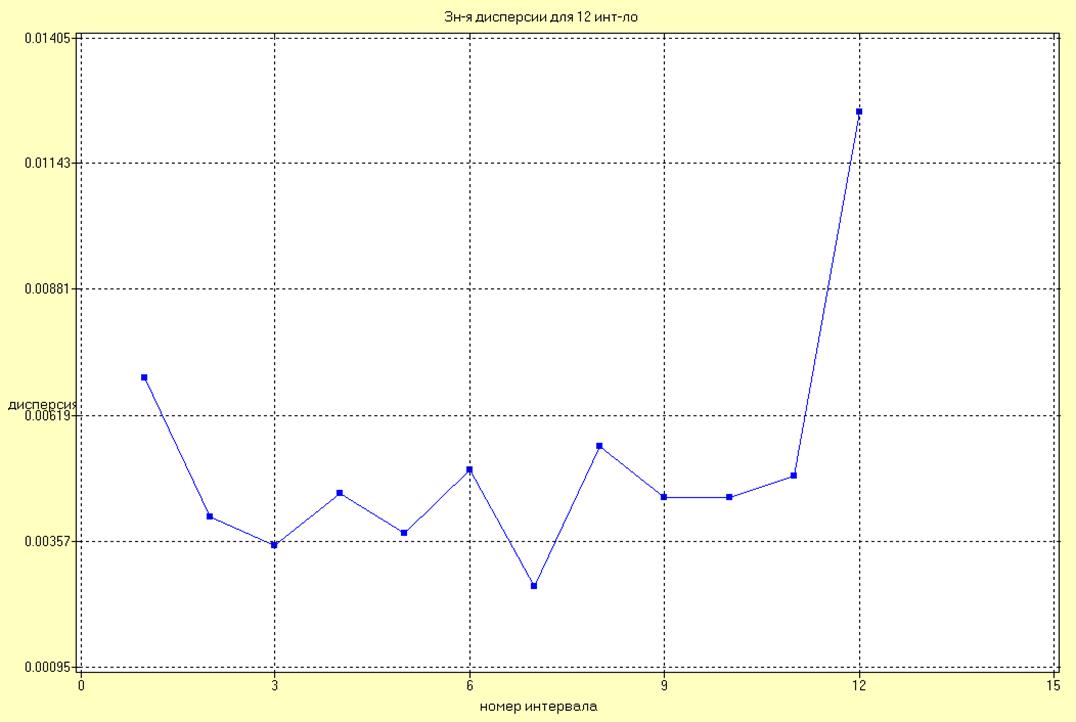
Рис.18. Значения дисперсий для всех интервалов

Проверка на  стационарность ряда:

Тесты на Случайность

                      Медианный Тест

  Переменная       Кол-во Серий     P-Значение      Длина Серий      P-Значение

o_h_w.mo           6               0.7630246006    3               0.8862304688   

o_h_w.disp         8               0.3657122963    2               0.9995117188   

                      Поворотных Точек Тест

  Переменная       Поворотных Точек Сред.Значение   Стан.Отклон.

o_h_w.mo           6               6.666666667     1.811111111    

o_h_w.disp         6               6.666666667     1.811111111    

Поворотных Точек Тест

                      Up & Down  Тест

  Переменная       Кол-во Серий     P-Значение      Длина Серий      P-Значение

o_h_w.mo           8               0.8043752738    3               0.8629557292   

o_h_w.disp         8               0.8043752738    3               0.8629557292   

По результатам всех тестов можно сделать вывод, что ряд является стационарным по математическому ожиданию и дисперсии.

Глава 2. Вторичный анализ стохастической составляющей

    Все последующие исследования проводятся для стационарного ряда, полученного после удаления из исходного ряда тренда и колебательных составляющих.

2.1 Анализ основных статистических характеристик временного ряда

Для ряда с удаленными трендом и колебательными составляющими рассчитаем основные статистические характеристики. Результаты представлены ниже. 

                                  Основные Статистики

                  o_h_w.filtrout0

Среднее значение  -0.001058206379

Медиана           -0.0009615950659

Максимум          0.2919238113   

Минимум           -0.4621696981  

Дисперсия         0.005233019512 

Станд.Откл.       0.07233961233  

Асимметрия        -0.2344181734  

Эксцесс           1.790745512    

2.2 Анализ вида распределения отсчетов временного ряда

Проверим гипотезу о нормальности распределения отсчетов временного ряда.  В ППП EVRISTA имеется метод, осуществляющий автоматическое тестирование данных временного ряда на соответствие определенному закону распределения. Результаты тестирования представлены ниже.

     Переменная d:\tr\o_h_w.filtrout0

       Критерий Хи-Квадрат Пирсона          Критерий Колмогорова-Смирнова  

     Распределение      Р-Значение        Распределение         Р-Значение 

Нормальное (A,B)        0               Нормальное (A,B)        0.000717992165 

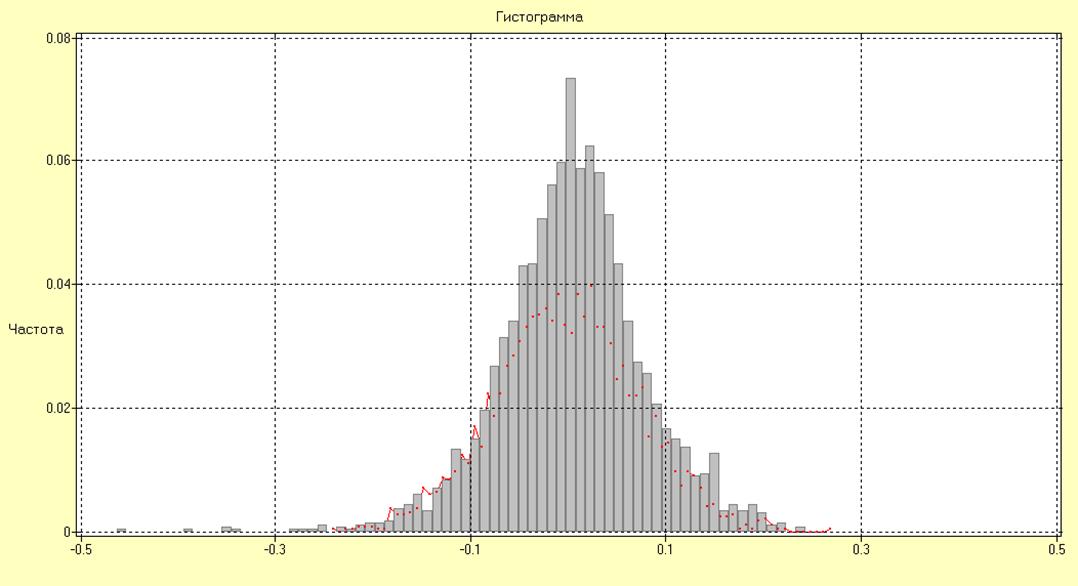
Рис. 12.Теоретическая и расчетная функции распределения.

                Критерий Хи-Квадрат Пирсона

_________________________________________________________________________________

     Переменная d:\tr\o_h_w.filtrout0

   Распределение        Статистика  Степени Свободы    P-Значение

Нормальное (A,B)        2660314.848     75              0              

          A =-0.001058206379 ,B =0.005233019512 

                Критерий Колмогорова-Смирнова

_________________________________________________________________________________

     Переменная d:\tr\o_h_w.filtrout0

   Распределение        Статистика      Р-Значение

Нормальное (A,B)        0.03635977421   0.0007179921628

          A =-0.001058206379 ,B =0.005233019512 

Результаты проведенного исследования отвергают гипотезу  о нормальном распределении отсчетов временного ряда.

2.3 Непараметрический анализ корреляционных свойств временного ряда

-5%

5%

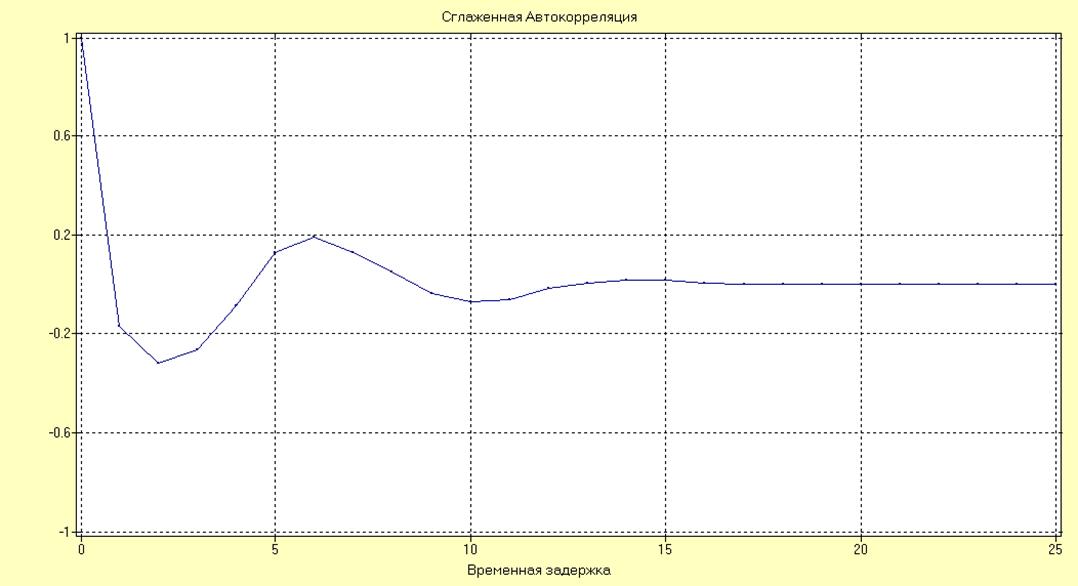
Рис. 13. Сглаженная автокорреляционная функция.

По графику определим максимальный интервал корреляции. Это время, после которого автокорреляционная функция попадает в 5% коридор. Для нашего случая это 11 отсчетов.

2.4 Непараметрический анализ спектральных свойств временного ряда

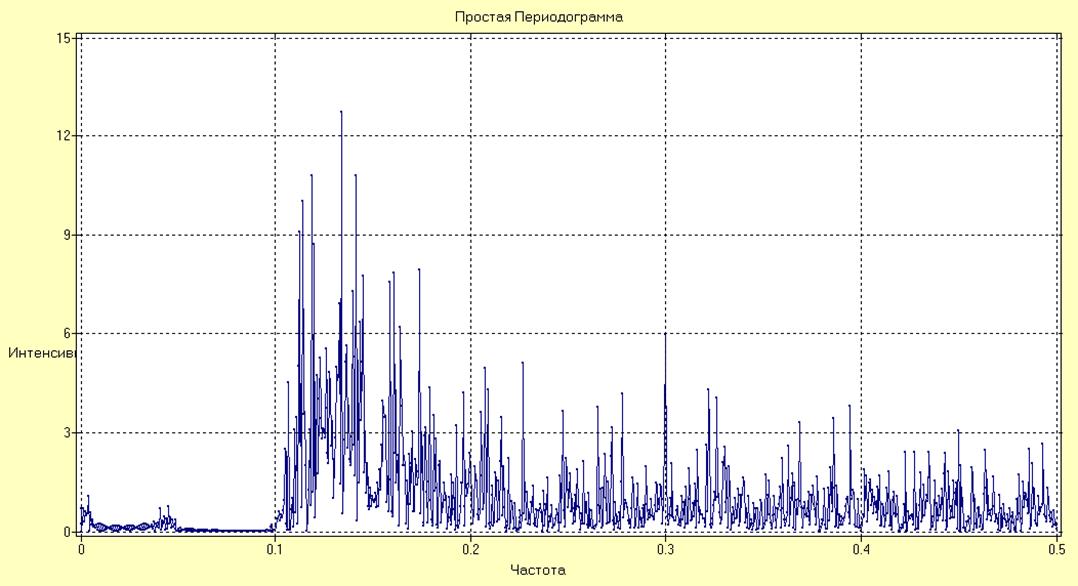
Рис. 14. Простая периодограмма.

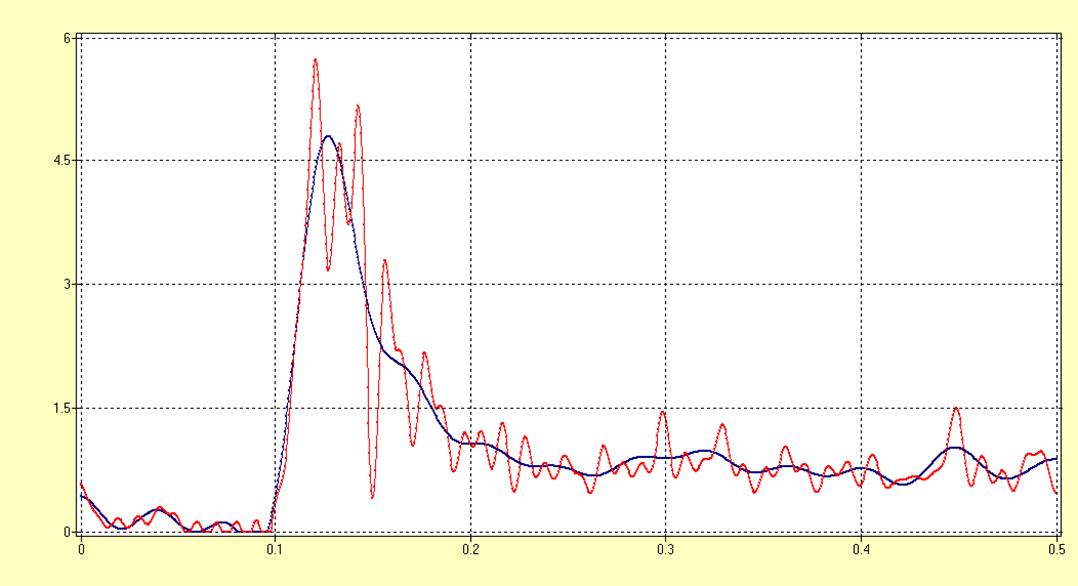
Рис. 15. Сглаженная СПМ c прямоугольным окном(25 и 99 точек).