Оценка среднего значения и дисперсии для указанных признаков. Вычисление матрицы частных коэффициентов. Проанализировать значения парного и частного коэффициентов корреляции

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Типовой расчет

по курсу «Идентификация и диагностика систем»

Выполнил
Студент	Попов И. О.
Вариант	10
Группа	А – 01 – 03
Дата	23.03.06

Принял
Преподаватель
Дата

Москва 2006 г.

Постановка задачи

Восемь регуляторов проходят опытные испытания в качестве устройства управления одним и тем же технологическим процессом автоматизированного разлива стали. При этом все регуляторы имеют различные технические характеристики, реализуют отличные друг от друга законы регулирования, выпущены различными заводами-изготовителями. Их функционирование характеризуется следующими показателями:

- переругулирование (в %);

- время регулирования (в сек.);

- стоимость (в тыс. руб.).

Номер регулятора
1	29	0,6	45
2	27	0,6	52
3	23	0,4	80
4	25	0,7	55
5	26	0,6	61
6	26	0,45	70
7	24	0,5	75
8	20	0,45	85

Расчетное задание включает следующие пункты.

1)  Оценить средние значения и дисперсии для признаков ,,. Рассчитать ковариационную и корреляционную матрицы для анализируемого трехмерного признака.

2)  Вычислить матрицу частных коэффициентов, т.е. оценить значения  (i≠k, l≠i, k≠l).

3)  Проанализировать значения парного  и частного  коэффициентов корреляции. Проверить гипотезу (при уровне значимости α=0,05) о их статистической значимости.

4)  Найти точечную оценку множественного коэффициента корреляции   и проверить гипотезу (при уровне значимости α=0,05) о его статистической значимости.

5)  Рассчитать коэффициенты парной регрессии и проверить значимость полученного уравнения (при уровне значимости α=0,05).

;

6)  Вывести уравнения для вычисления главных компонент ,,по заданным значениям исходных показателей  ,, (для вычисления корней полинома третьей степени рекомендуется использовать пакет прикладных программ (ППП) MATLAB).

7)  Определить относительные доли суммарной дисперсии, обусловленные одной и двумя главными компонентами.

8)  Проверить проведенные расчеты с помощью ППП STATISTICA.

9)  Провести дополнительные исследования заданной выборки с помощью ППП STATISTICA, используя

-  иерархический кластерный анализ;

-  многомерное шкалирование.

Решение

1)  Оценим средние значения и дисперсии для признаков ,,:

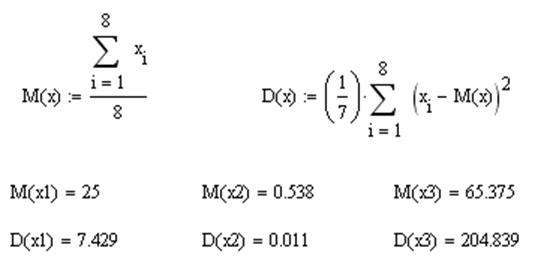
Рассчитаем ковариационную матрицу для анализируемого трехмерного признака:

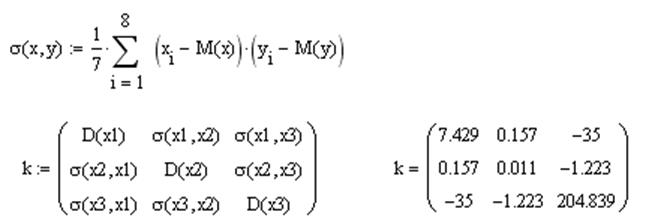
И корреляционную:

2)  Оценим значения частных коэффициентов корреляции ,  и :

3)  Парный коэффициент корреляции  характеризует наличие линейной зависимости между переменными  и  и силу взаимосвязи между ними. Значение  = -0.897 говорит о возможном наличии обратно-пропорциональной зависимости между исследуемыми признаками. Проверим гипотезу о его статистической значимости (при уровне значимости α=0,05):

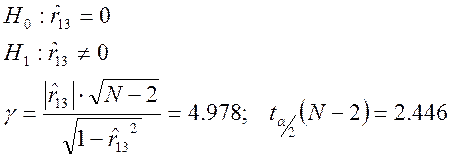
Т.к. , то гипотеза  отклоняется, и, следовательно, коэффициент  значимый.

Частный коэффициент корреляции  характеризует линейную взаимосвязь между переменными  и  и силу этой взаимосвязи при фиксированном значении . Значение  = -0.937 говорит о наличии взаимосвязи между переменными  и . Проверим гипотезу о его статистической значимости (при уровне значимости α=0,05):

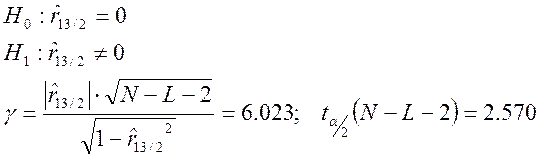
Т.к. , то гипотеза  отклоняется, и, следовательно, коэффициент  значимый.

4)  Найдем точечную оценку множественного коэффициента корреляции  :

 и проверим гипотезу (при уровне значимости α=0,05) о его статистической значимости:

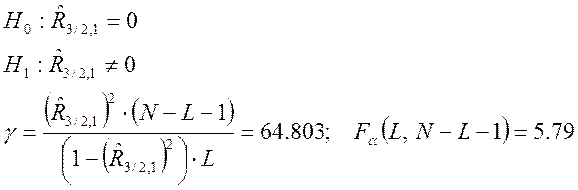
Т.к. , то гипотеза  отклоняется, и, следовательно, коэффициент  значимый.

5)  Рассчитаем коэффициенты парной регрессии:

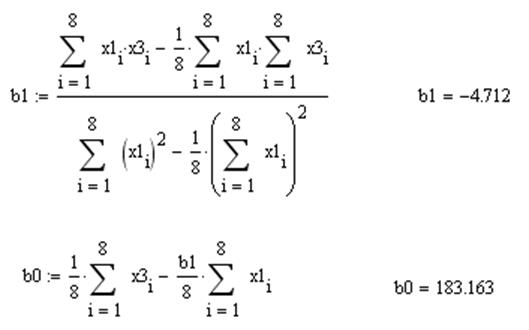
и проверим значимость полученного уравнения  (при уровне значимости α=0,05):

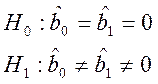
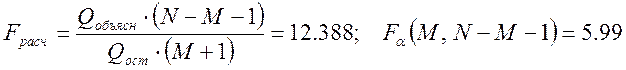
Т.к. , то гипотеза  отклоняется, и, следовательно, регрессия значима.

Рассчитаем коэффициент детерминации:

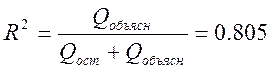
Значение близко к 1, следовательно, связь  и  действительно существует.

6)  Выведем уравнения для вычисления главных компонент ,,по заданным значениям исходных показателей  ,,:

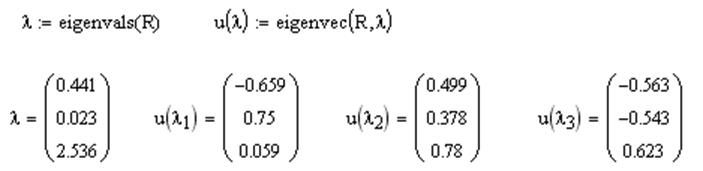
где  - собственные числа корреляционной матрицы R, а  - соответствующие им собственные вектора.

Главные компоненты могут быть найдены по формулам:

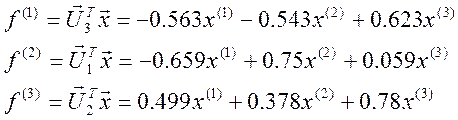
7)  Определим относительные доли суммарной дисперсии, обусловленные одной главной компонентой:

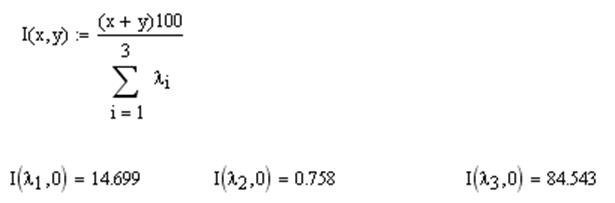
и двумя главными компонентами:

Т.о. 84% суммарной дисперсии обусловлено главной компонентой , а  и  обуславливают 99% суммарной дисперсии.

Проверка проведенных расчетов с помощью ППП STATISTICA

Средние значения для признаков:

Совпадают с рассчитанными ранее.

Ковариационная матрица

Дисперсии признаков и элементы ковариационной матрицы совпадают с рассчитанными ранее.

Корреляционная матрица (отмеченные коэффициенты значимы при α=0,05)

Элементы корреляционной матрицы совпадают с рассчитанными ранее. Парный коэффициент корреляции  значимый.

Частные коэффициенты корреляции (отмеченные коэффициенты значимы при α=0,05)

Значения совпадают с рассчитанными ранее. Частный коэффициент корреляции  значимый.

Результаты множественной регрессии:

Множественный коэффициент корреляции   значимый при α=0,05, т.к. 0,00027 < 0,05.

Для парной регрессии:

Коэффициенты парной регрессии совпадают с рассчитанными ранее.

Значение коэффициента детерминации совпадает с рассчитанным ранее

Главные компоненты:

Коэффициенты, входящие в выражение для вычисления главных компонент совпадают с рассчитанными ранее.

Относительные доли суммарной дисперсии совпадают с рассчитанными ранее.

Дополнительные исследования заданной выборки с помощью ППП STATISTICA

Иерархический кластерный анализ:

Матрица расстояний имеет вид (Евклидово расстояние, одиночная связь):

	Var1	Var2	Var3	Var4	Var5	Var6	Var7	Var8
Var1	0,00000	7,28011	35,51113	10,77079	16,27882	25,17980	30,41398	41,00027
Var2	7,28011	0,00000	28,28498	3,60694	9,05539	18,02838	23,19504	33,73459
Var3	35,51113	28,28498	0,00000	25,08167	19,23642	10,44043	5,10000	5,83117
Var4	10,77079	3,60694	25,08167	0,00000	6,08358	15,03537	20,02598	30,41484
Var5	16,27882	9,05539	19,23642	6,08358	0,00000	9,00125	14,14249	24,73909
Var6	25,17980	18,02838	10,44043	15,03537	9,00125	0,00000	5,38540	16,15549
Var7	30,41398	23,19504	5,10000	20,02598	14,14249	5,38540	0,00000	10,77045
Var8	41,00027	33,73459	5,83117	30,41484	24,73909	16,15549	10,77045	0,00000

Дендрограмма для этого случая:

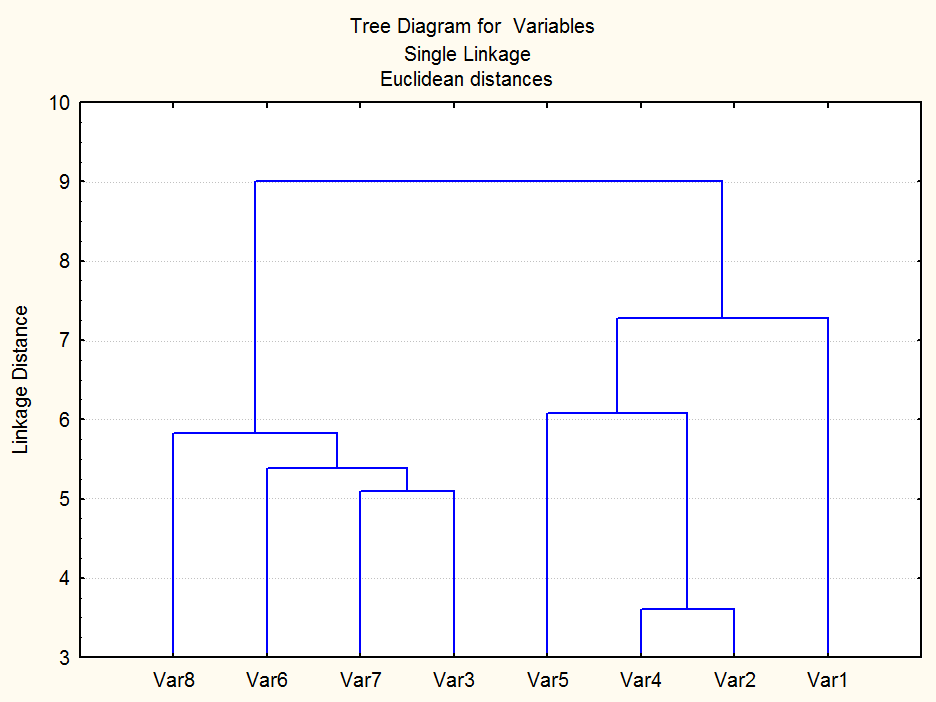
Можно выделить два кластера:  и .

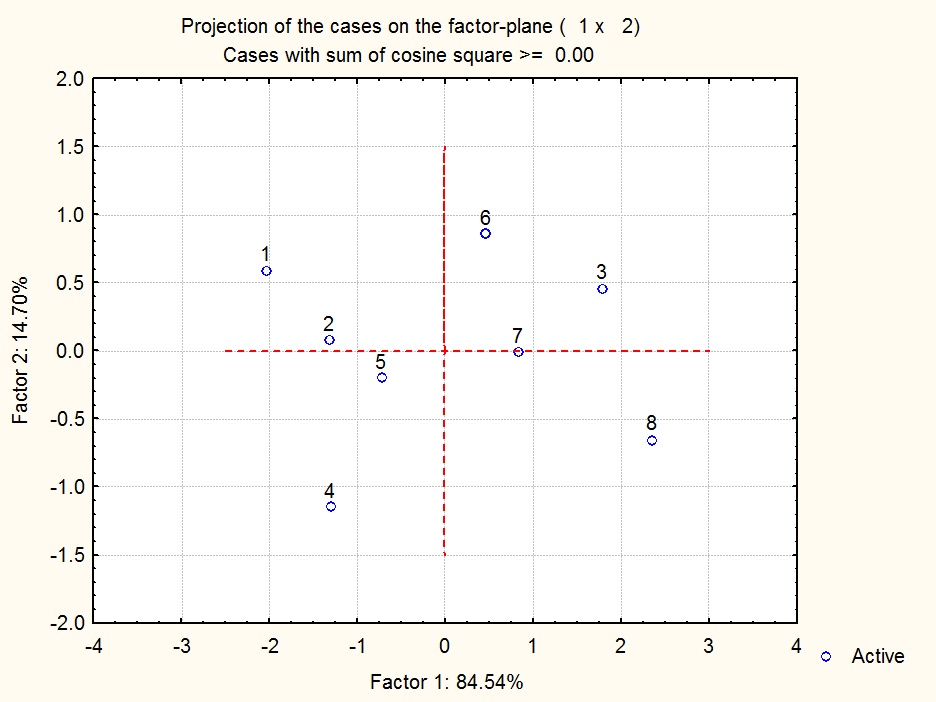
Многомерное шкалирование:

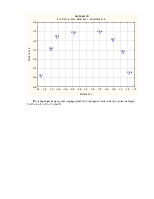
Проекция на плоскость имеет вид:

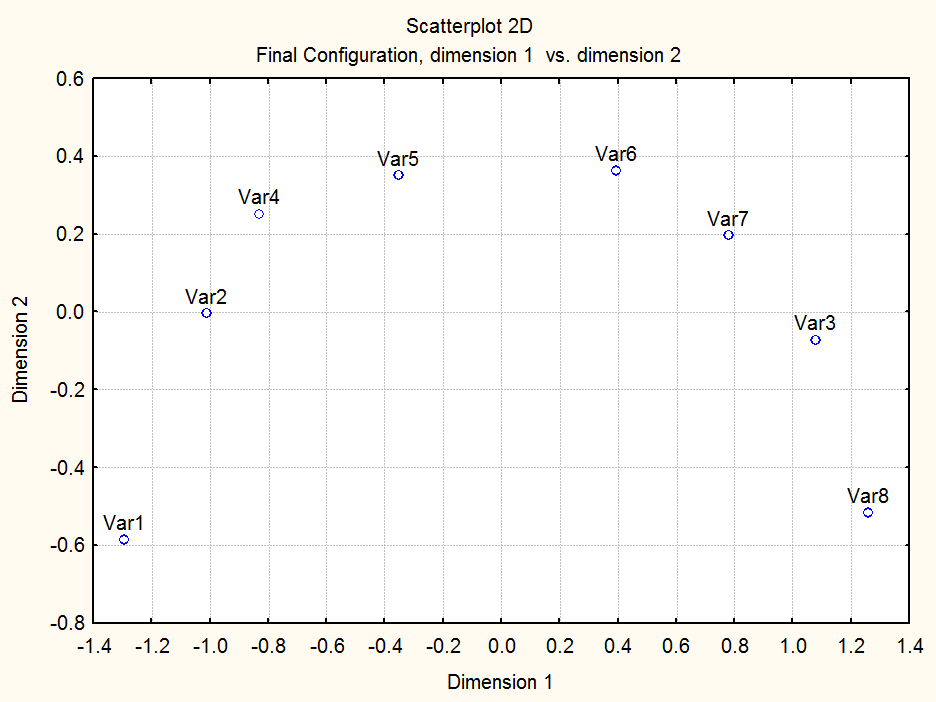
Подтверждается результат иерархического кластерного анализа об одном кластере:  и .