Исследование методов классификации многомерных данных, страница 5

Апостериорная вероятность - вероятность того, что образец принадлежит к конкретной совокупности. Это значение будет не вполне точным, так как распределение вокруг среднего для каждой совокупности будет не в точности нормальным.

Построим канонические дискриминантные функции (КДФ):

Для визуализации данных будут использоваться две КДФ. Построим отображение исходной выборки в пространство первой и второй КДФ:

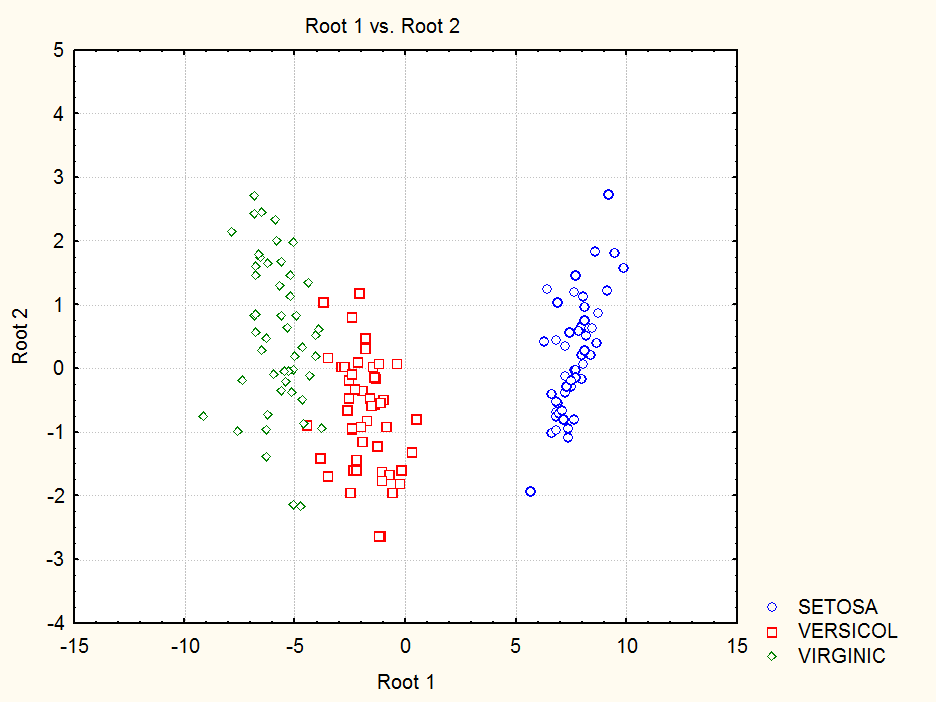
Разброс значений объясняет в основном первая КДФ. Она разделяет класс SETOSA от объединения классов VERSICOL и VERGINIC. Вторая КДФ разделяет классы VERSICOL и VERGINIC.

Метод деревья решений

Произведем классификацию элементов исследуемой выборки с помощью метода деревья решений. Дерево решений имеет вид:

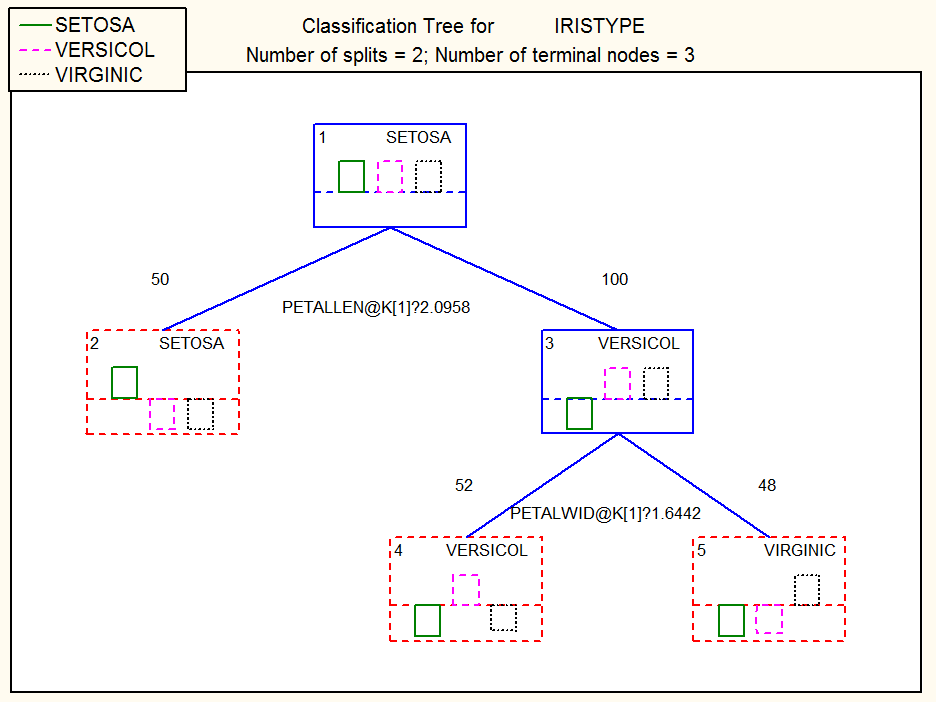
Из приведенных данных видно, что общая совокупность наблюдений имеет свойства, близкие к классу SETOSA. При более детальном рассмотрении происходит выделение совокупности по свойствам, близкой к классу VERSICOL, которая далее разделяется на 2 класса. Окончательно выделяется 3 класса.

Проанализируем качество классификации:

	Left	Right	n in cls SETOSA	n in cls VERSICOL	n in cls VIRGINIC	Predict.
1	2	3	50	50	50	SETOSA
2			50	0	0	SETOSA
3	4	5	0	50	50	VERSICOL
4			0	48	4	VERSICOL
5			0	2	46	VIRGINIC

Из приведенных данных видно, что ошибочно проклассифицированы 6 элементов из 150.

Проанализируем дискриминантные свойства переменных:

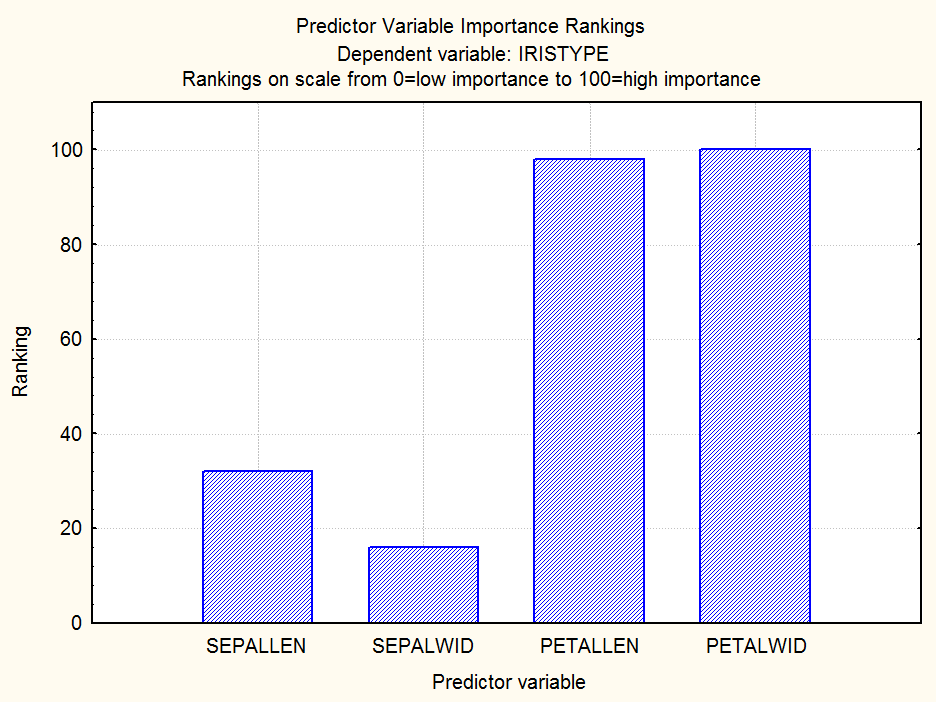
Из приведенного графика видно, что наибольшей значимостью с точки зрения влияния на результат классификации, обладают признаки PETALLEN и PETALWID, а у SEPALLEN и SEPALWID эта значимость небольшая.

Выводы

Сравнивая результаты, полученные в ходе исследования исходной выборки методами дискриминантного анализа и деревья решений, можно сделать вывод о том, что более точную классификацию удается получить с помощью метода дискриминантного анализа. С помощью метода деревья решений в данном случае производится менее точная классификация.