Исследование методов классификации многомерных данных, страница 2

Проверка предположений дискриминантного анализа

а)  о нормальности

б)  о линейной независимости и равенстве корреляционных матриц классов

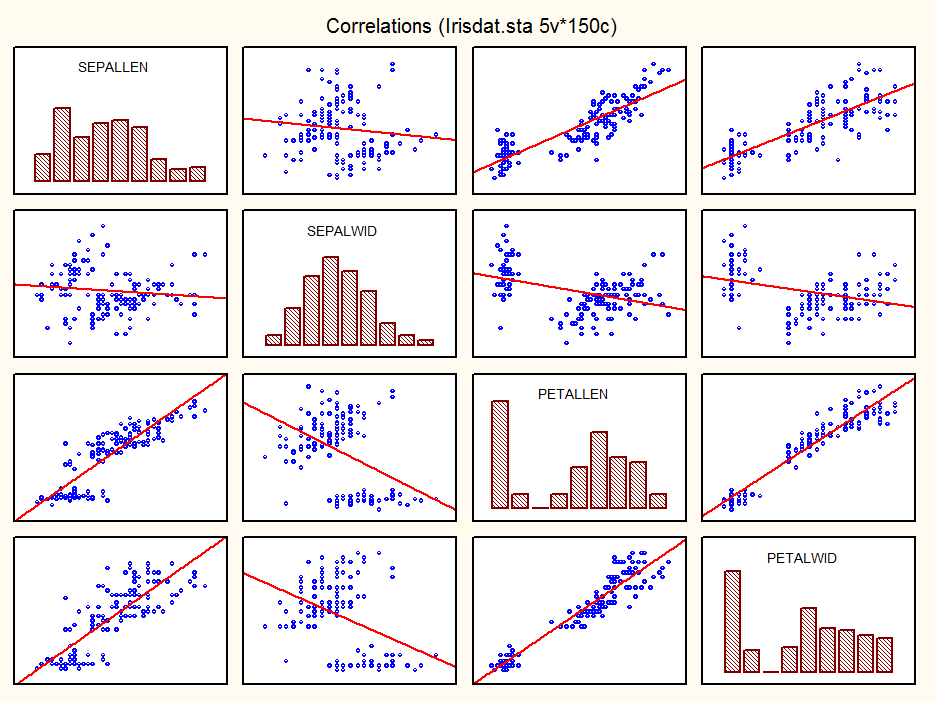
Из приведенных гистограмм можно сделать вывод о том, что признаки SEPALLEN и SEPALWID имеют распределение близкое к нормальному, а в распределении признаков PETALLEN и PETALWID имеются небольшие отклонения от нормального, однако, можно считать, что предположение о нормальности выполняется.

Так же можно заметить, что наиболее зависимыми будут признаки PETALLEN и PETALWID. Но в целом, предположение о линейной независимости признаков и равенстве корреляционных матриц классов выполняется.

Стандартный метод дискриминантного анализа

Стандартный метод дискриминантного анализа дает следующие результаты:

	Wilks'	Partial	F-remove	p-level	Toler.	1-Toler.
SEPALLEN	0,024976	0,938464	4,72115	0,010329	0,347993	0,652007
SEPALWID	0,030580	0,766480	21,93593	0,000000	0,608859	0,391141
PETALLEN	0,035025	0,669206	35,59018	0,000000	0,365126	0,634874
PETALWID	0,031546	0,743001	24,90433	0,000000	0,649314	0,350686

Классифицирующие функции имеют вид:

Коэффициенты, с которыми в классифицирующие функции входят признаки PETALLEN и PETALWID существенно различаются, что говорит об их более весомом вкладе в результат классификации.

Проанализируем обобщенные расстояния Махаланобиса: