Дифференциальные уравнения (расчетно-графическое задание), страница 3

  

тогда первоначальное уравнение примет вид:

;          ;          

тождество подтвердилось, значит уравнение решено верно.

4.  Найти частное решение, удовлетворяющее заданному условию.

Чтобы найти частное решения найдём производную нашей функции(y) и подставить начальные условия в (y) и   

Получим систему уравнений:

      

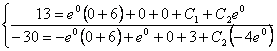
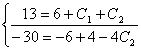
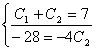
тогда получим частное решение(ЧР):

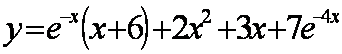
5.  Выполнить проверку частного решения.

Для того чтобы выполнить проверку частного решения(п.4) необходимо найти первую и вторую производные и подставить их в первоначальное уравнение():

тогда наше главное уравнение примет вид:

;             

тождество подтвердилось, значит уравнение решено верно.

6.  Построить график частного решения.