в)
(2) напомним: 
,
,где
z=1, т.к. 
(a=0, b=0) тогда
найдём
первую и вторую производные:
в уравнение(2) подставим значения
и 
помножив
их на коэффициенты:
По
условию 
тогда
2. Найдём решение методом вариации постоянных (
и 
).
составим систему Ла-Гранжа:
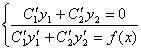, где 
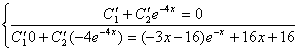
(2)
(1)
]
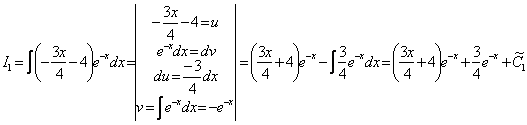
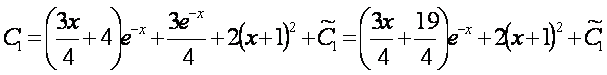
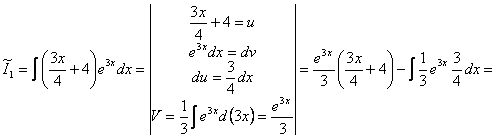
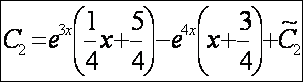
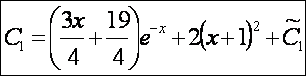
теперь найдём
неизвестную(
) по уже давно забытой формуле:
:
(это и будет окончательный ответ общего решения(ОР))
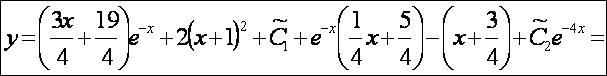
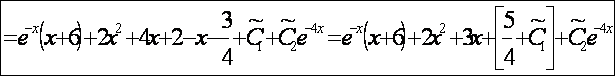
если константу в квадратных скобках принять за другую постоянную, то всё сходится, и примерчик решён верно.
3. Выполнить проверку общего решения.
Для того чтобы проверить общее решение надо найти
первую и вторую производные от общего решения(ОР) и подставить в первоначальное
уравнение(
):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.