Анализ и синтез на базе комплекса технических средств гипотетической микропроцессорной системы оптимального управления технологическим процессом и оборудованием технического объекта (Кристаллизатор), страница 5

Для модели относительно y1 Для модели относительно y2 b0 3,29 6,54 b1 0,43 0,21 b2 0,38 0,26 b3 0,38 0,21 b4 0,23 0,21 Табл.1.3

Для модели относительно y1 Для модели относительно y2 b0 0,06 3,08 b1 0,86 0,42 b2 0,76 0,52 b3 0,76 0,42 b4 -0,46 0,42 Табл.1.4

Полученные регрессионные модели:

y1(U1,U2,x1,x2)=0.06+0.860*U1+0.76*U2+0.76*x1-0.46*x2                                          (2)

y2(U1,U2,x1,x2)=3.08+0.42*U1+0.52*U2+0.42*x1+0.42*x2                                           (3)

Оптимизация по регрессионным моделям

По полученной в предыдущем пункте регрессионной модели для оценивания наблюдения отклика объекта y2, который выбран за критерий, найдем оптимальную точку. Для нахождения оптимальной точки при данном критерии и ограничениях воспользуемся программой входящей в пакет прикладных программ по оптимизации и моделированию в условиях неопределенности. Для этого введем в программу целевую функцию (3) и ограничения:

y1(U1,U2,x1,x2)=0.06+0.860*U1+0.76*U2+0.76*x1-0.46*x2            max

1.5<U1<2.5                                                                                                               (4a)

0.5<U2<1.5                                                                                                                                    (4б)

   2<X1<3                                                                                                                  (4в)

   2<X2<3                                                                                                                  (4г)

0.42*u1+0.520*u2+0.42*x1+0.42*x2<4.35                                                            (4д)

Так же исследуем на оптимальность функции y_1-(u1,u2,x1,x2) и y₁₊(u1,u2,x1,x2) с нижними и верхними значениями коэффициентов, которые расcчитываются по формулам:

Данное исследование производиться для исследования устойчивости оптимального решения к ошибкам

Следовательно, получаем варьирование коэффициентов регрессионной модели для y1:

Коэффициенты	Базовый уровень	Нижний уровень	Верхний уровень	Дисперсия
B0	0.06	0.012671	0.107329	0.00056
B1	0.86	0.812671	0.907329	0.00056
B2	0.76	0.712671	0.807329	0.00056
B3	0.76	0.712671	0.807329	0.00056
B4	-0.46	-0.6594	-0.2606	0.00994

И для y2:

Коэффициенты	Базовый уровень	Нижний уровень	Верхний уровень	Дисперсия
B0	3.08	3.032671	3.127329	0.00056
B1	0.42	0.372671	0.467329	0.00056
B2	0.52	0.472671	0.567329	0.00056
B3	0.42	0.372671	0.467329	0.00056
B4	0.42	0.220601	0.619399	0.00994

И модели регрессии:

Целевые функции	y1-(u1,u2,x1,x2)  =0,01+0,81*u1+0.713*u2+0.713*x1-0.66x2 y1(u1,u2,x1,x2)   =0.06+0.86*u1+0.76*u2+0.76*x1-0.46*x2 y1+(u1,u2,x1,x2)  =0.11+0.91*u1+0.81*u2+0.81*x1-0.26*x2
Ограничения	1.5<U1<2.5 0.5<U2<1.5    2<X1<3    2<X2<3
	y2-(u1,u2,x1,x2)  =3.03+0.37*u1+0.47*u2+0.37*x1+0.22*x2 y2(u1,u2,x1,x2)   =3.08+0.42*u1+0.52*u2+0.42*x1+0.42*x2 y2+(u1,u2,x1,x2)  =3.13+0.47*u1+0.57*u2+0.47*x1+0.62*x2

Решение для функции базового уровня

1)Загрузка задачи

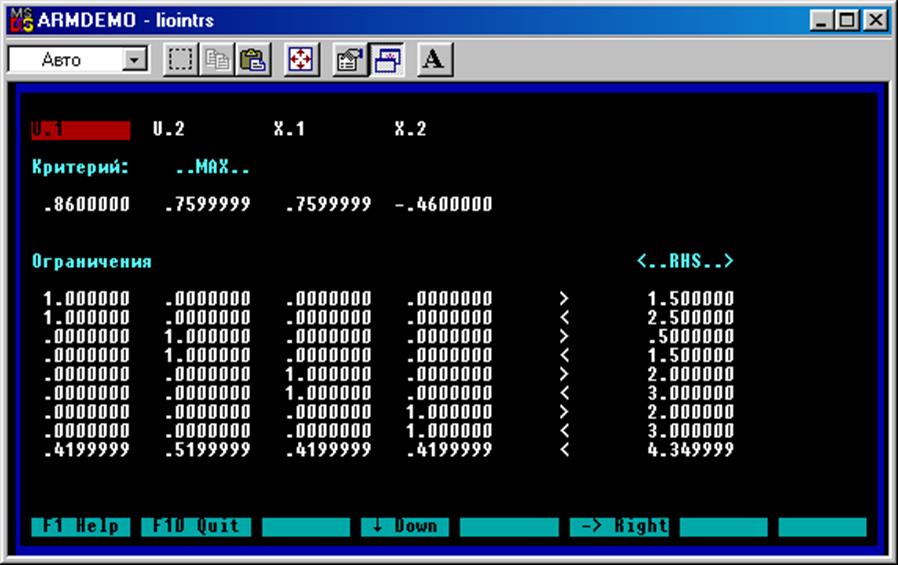
2)Решение

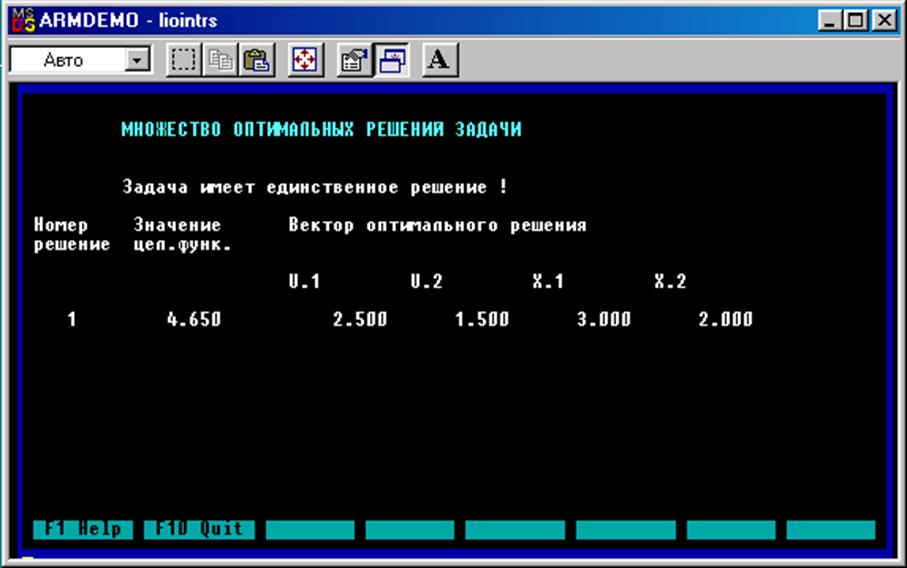
Решение для функции нижнего уровня

1)Загрузка задачи

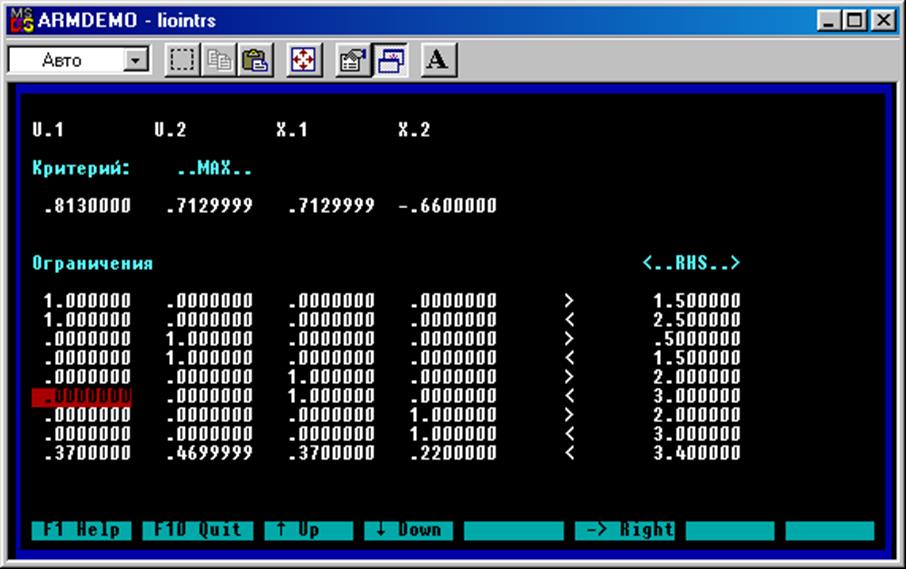
2)Решение

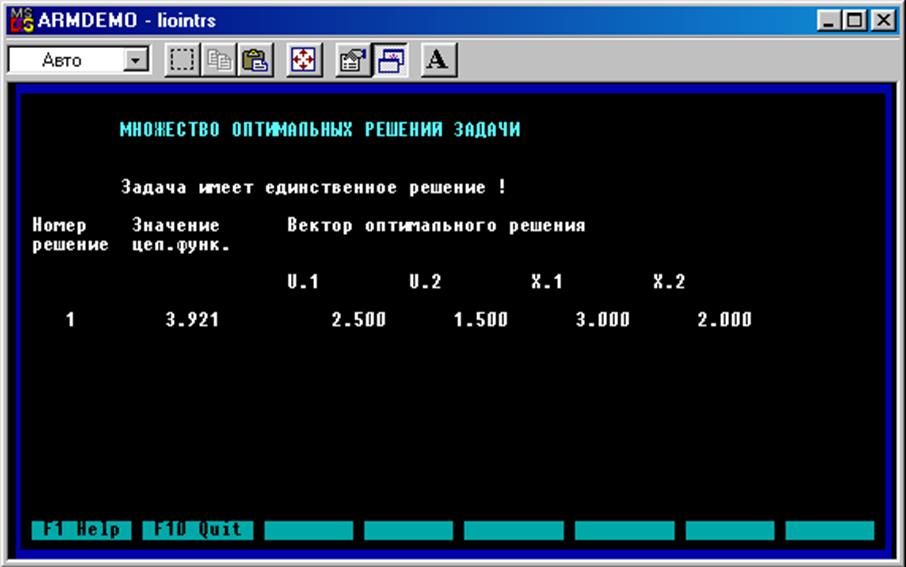
Решение для нижней целевой функции

1)Загрузка задачи

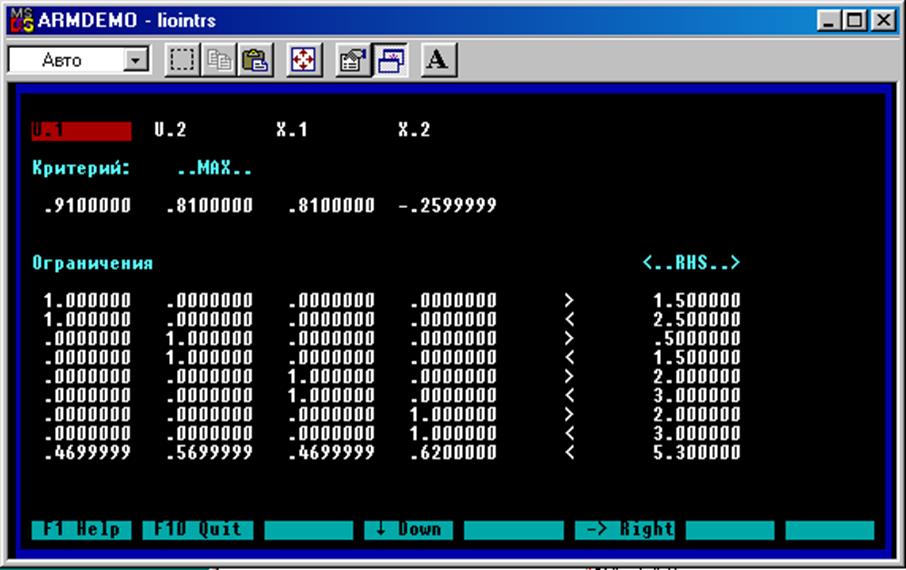
2)Решение

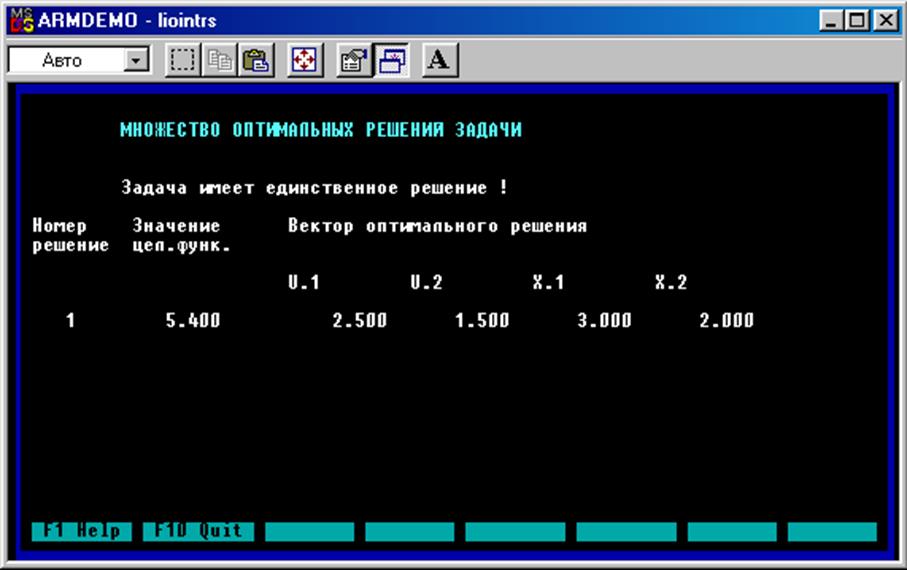
По данным прикладной программы получили следующие оптимальные точки (значения скорректированы с учетом свободного члена в целевых функциях):

По результатам программы получено решение задачи оптимизации:

U1=2.5            U2=1.5            X1=3               X2=2

Модели регрессии	Max	U1	U2	X1	X2
y1-(u1,u2,x1,x2)  =	3,931	2.5	1.5	3	2
y1(u1,u2,x1,x2)  =	4,71	2.5	1.5	3	2
y1+(u1,u2,x1,x2) =	5,51	2.5	1.5	3	2

Вывод: Для поддержания оптимальности работы объекта необходимо поддерживать значения регулируемых параметров на верхнем уровне: u1=2.5, u2=1.5

Предлагаемый комплекс технических средств