Анализ и синтез на базе комплекса технических средств гипотетической микропроцессорной системы оптимального управления технологическим процессом и оборудованием технического объекта (Кристаллизатор), страница 3

3)  Снимаем данные со всех выходных переменных.

Недостатком данного эксперимента может являться невозможность точного варьирования и фиксации факторов (например, из-за того, что они являются неуправляемыми, или из-за наличия шумов и дрейфа). Мы применяем этот метод для нашего учебно – исследовательского комплекса, работающего в режиме эксперимента.

Выявление зависимости выходных переменных от X1

 (Данные эксперимента находятся в файле KRISTALL.I4)

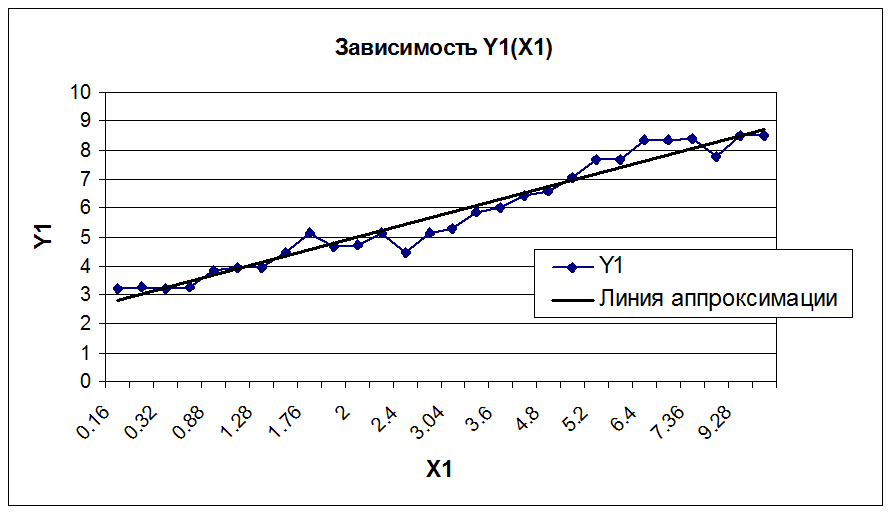
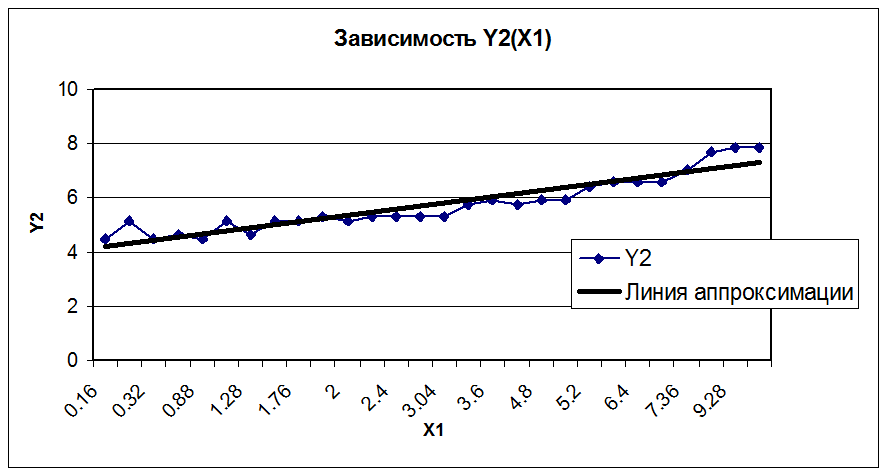
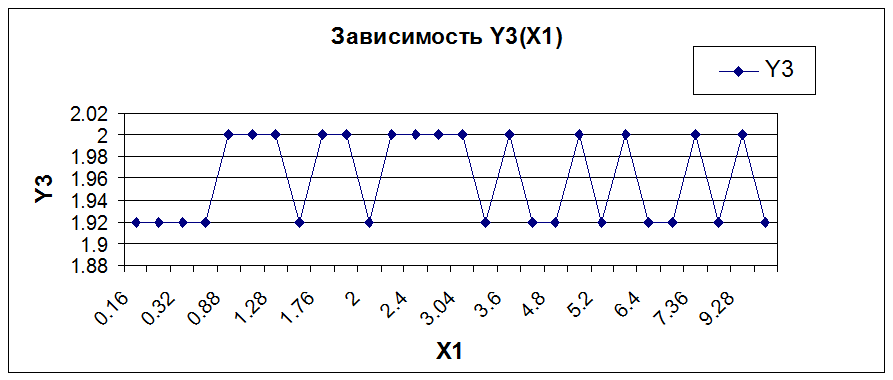
Вывод:

Из графиков видно, что Y1 и Y2 зависят от X1 линейно, причем с увеличением X1 увеличивается как Y1, так и Y2. Y3 от X1 не зависит (вид зависимости не определен) ,или зависимость является нелинейной.

Выявление зависимости выходных переменных от X2

(Данные эксперимента находятся в файле KRISTALL.I9)

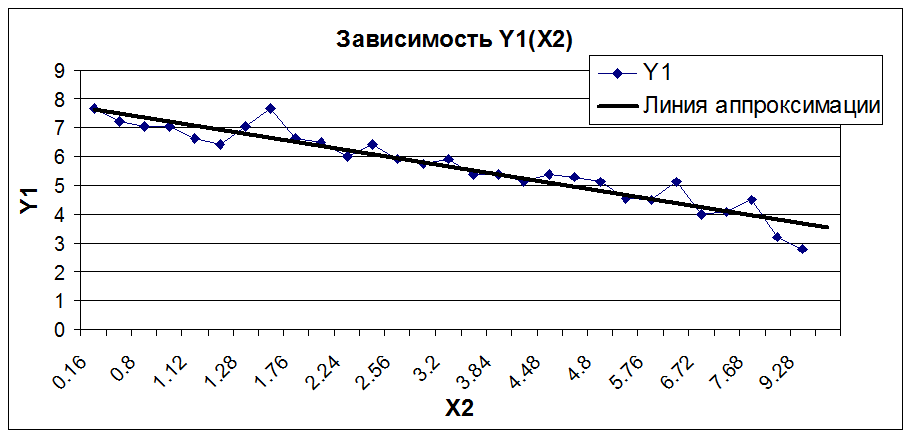
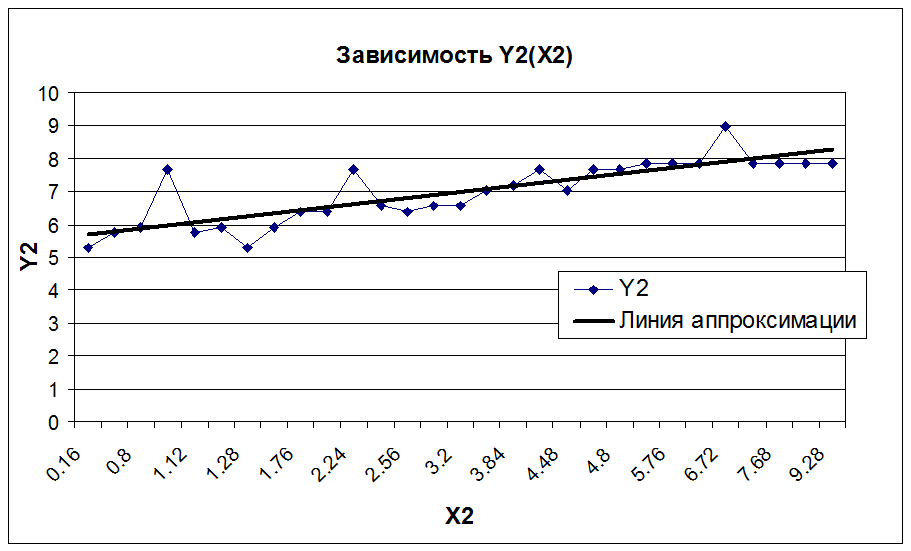
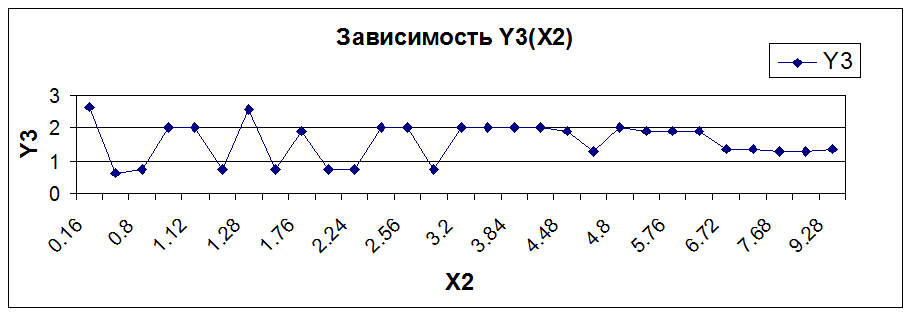
Вывод:

Как видно из графиков, Y1 и Y2 зависят от X2 линейно, причем с увеличением X2 Y1 уменьшается, а Y2 увеличивается. Y3 от X2 не зависит (вид зависимости не определен) .

Выявление зависимости выходных переменных от U1

(Данные эксперимента находятся в файле (файл KRISTALL.I10)

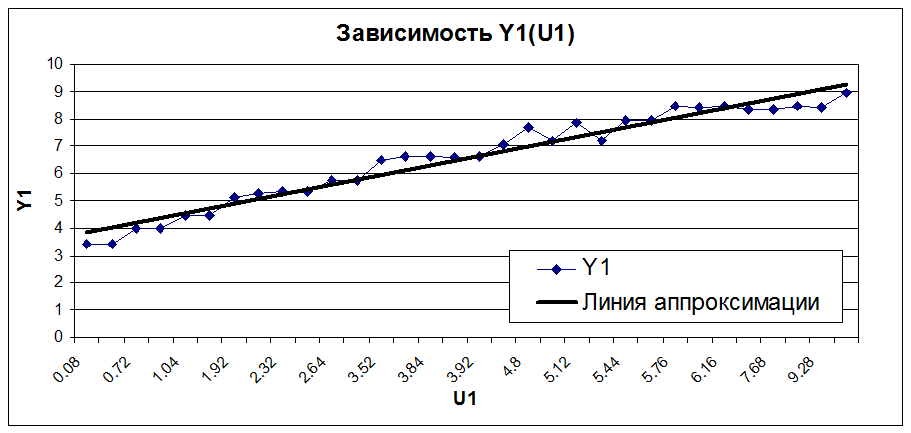
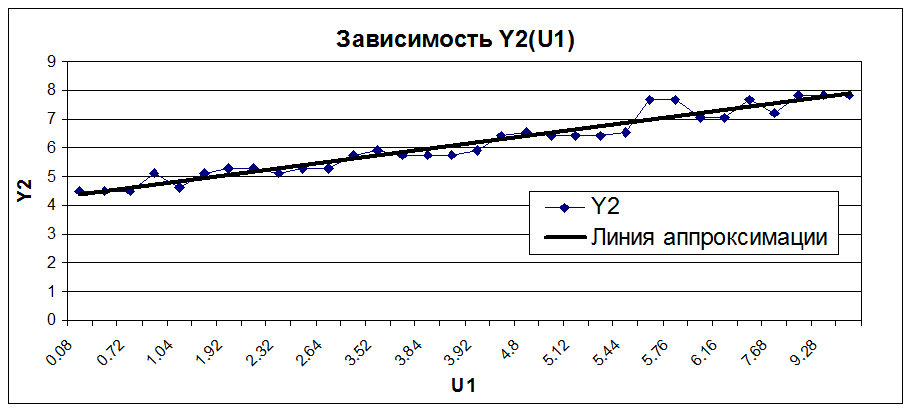
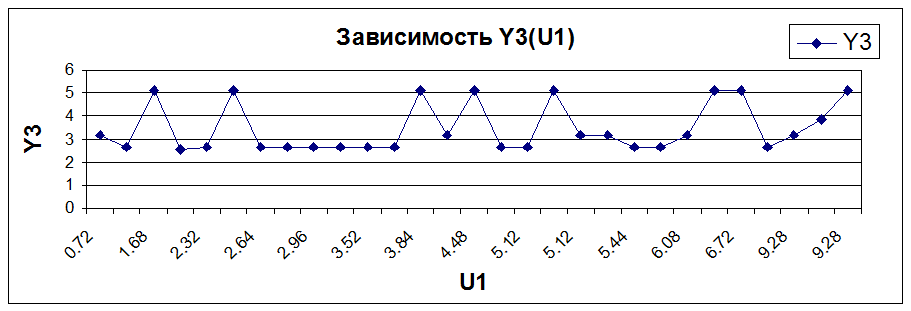
Вывод:

Из графиков видно, что Y1 и Y2 зависят от U1 линейно, причем с увеличением U1 увеличивается как Y1, так и Y2. Y3 от U1 не зависит (вид зависимости не определен).

Выявление зависимости выходных переменных от U2

(Данные эксперимента находятся в файле KRISTALL.I7)

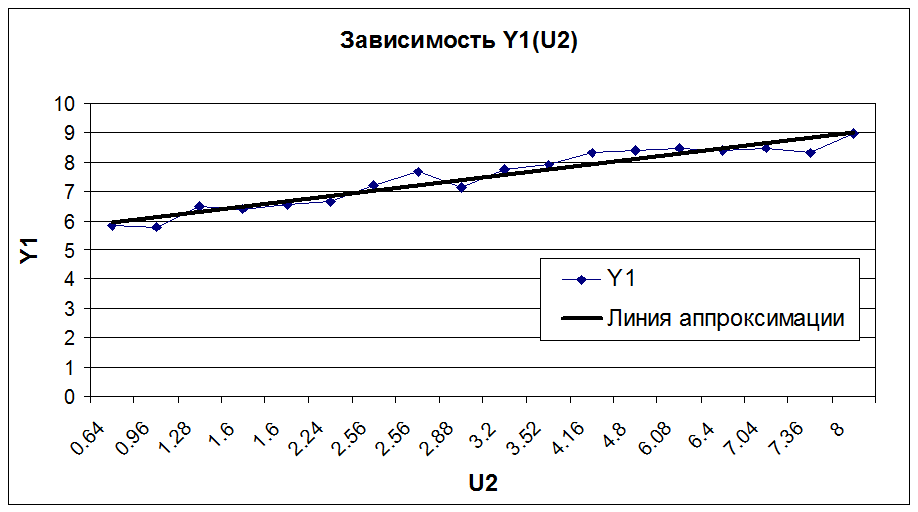
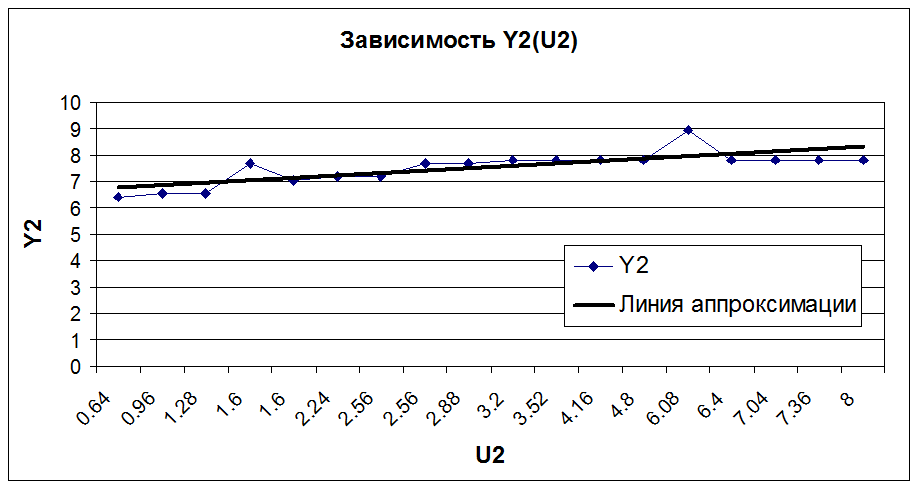
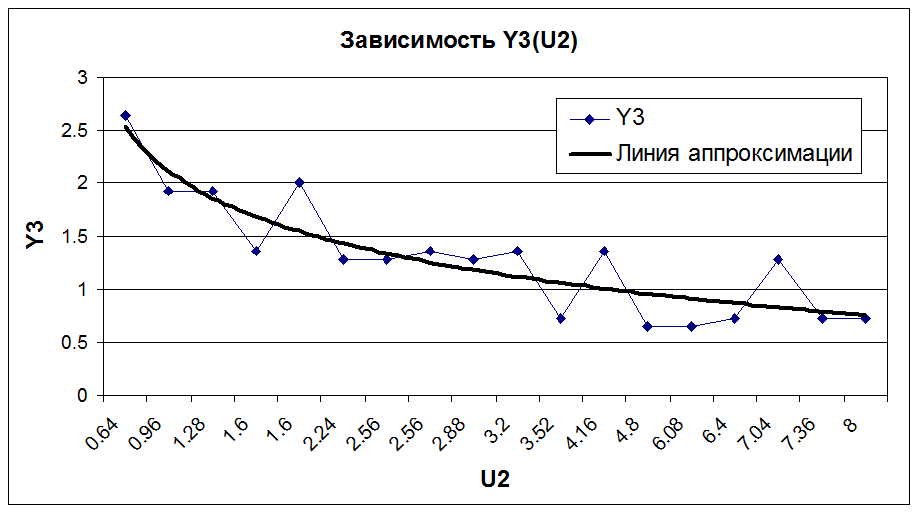
Из графиков видно, что от U2 зависят не только Y1 и Y2, но и Y3. Причем Y1 и Y2 зависят от U2 линейно, а Y3 динамически. При этом с увеличением U2 Y1 и Y2 увеличиваются, а Y3 уменьшается.

Так как при изменении параметров U1 и U2 Y1 и Y2 изменяются, то объект является многосвязным

Не все выявленные зависимости – линейны, а значит объект нельзя считать линейным.

Изучение стационарности объекта (KRISTALL.I2, KRISTALL.I3)

Первый съем данных

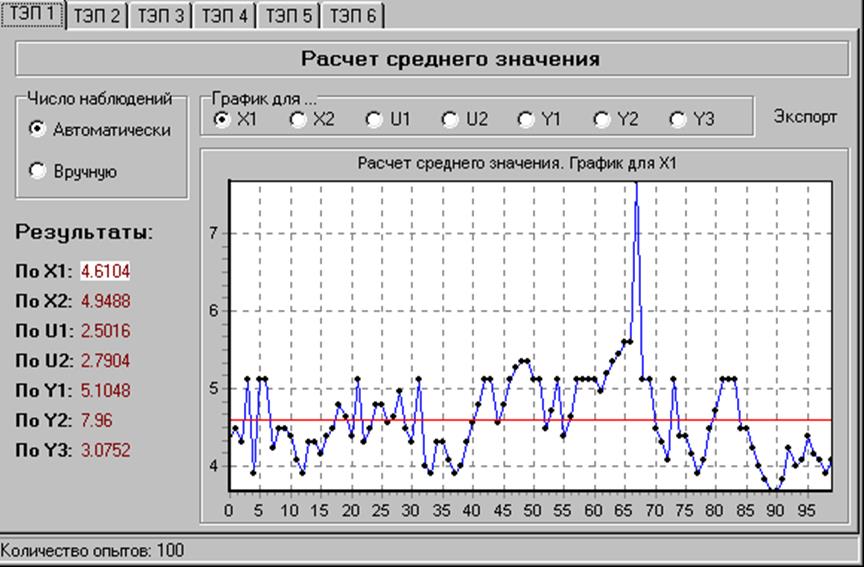
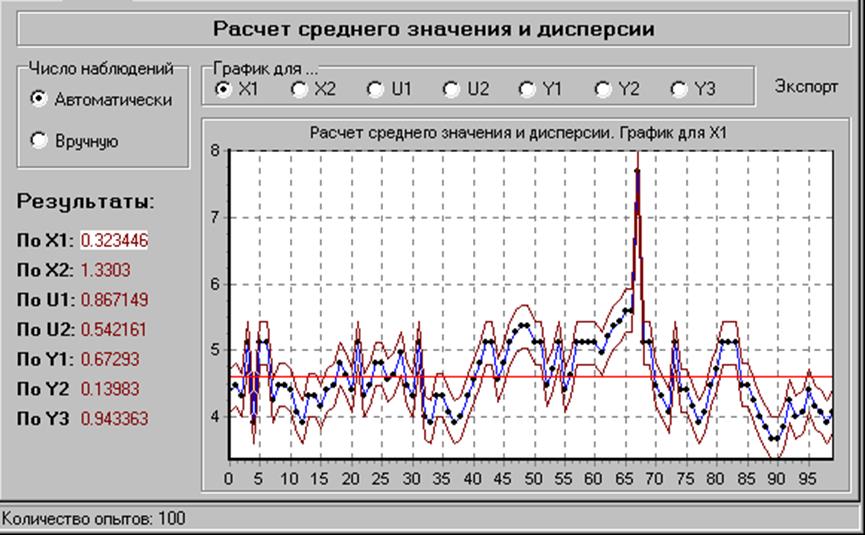
Повторный съем данных

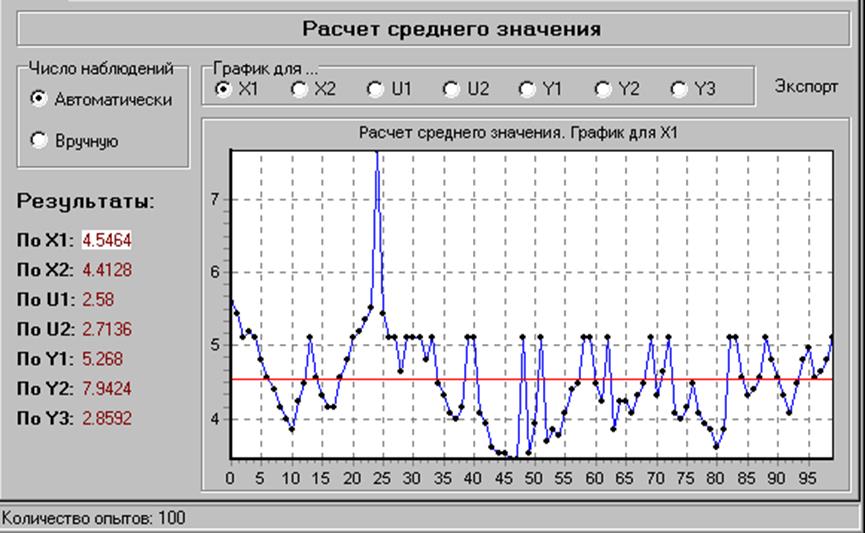
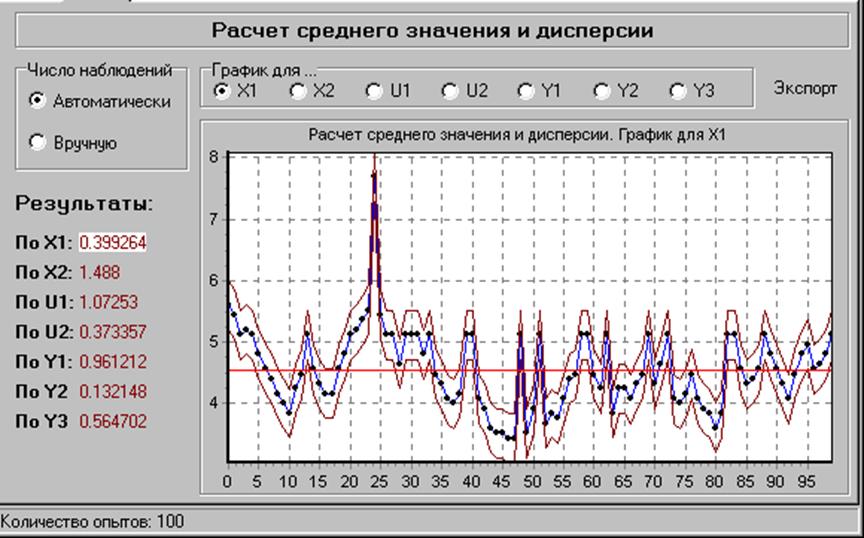
При первом съеме: M[Y1]=5.1048, M[Y2]=7.96, M[Y3]=3.0752

При повторном съеме: M[Y1]=5.268, M[Y2]=7.9424, M[Y3]=2.8592

По данным эксперимента видно, что средние значения выходных переменных близки между собой, не смотря на то, что между съемами данных прошел значительный промежуток времени, а значит можно сделать вывод:

переменные Y1,Y2 – тсационарные

переменная Y3 - нестационарная

Исходя из представленных выше графиков, легко видеть, что характер изменения контролируемых, но неуправляемых в режиме нормальной эксплуатации возмущений случайный.

Блок-схема комплекса

По результатам анализа связей между входными и выходными величинами можно построить следующую блок – схему комплекса

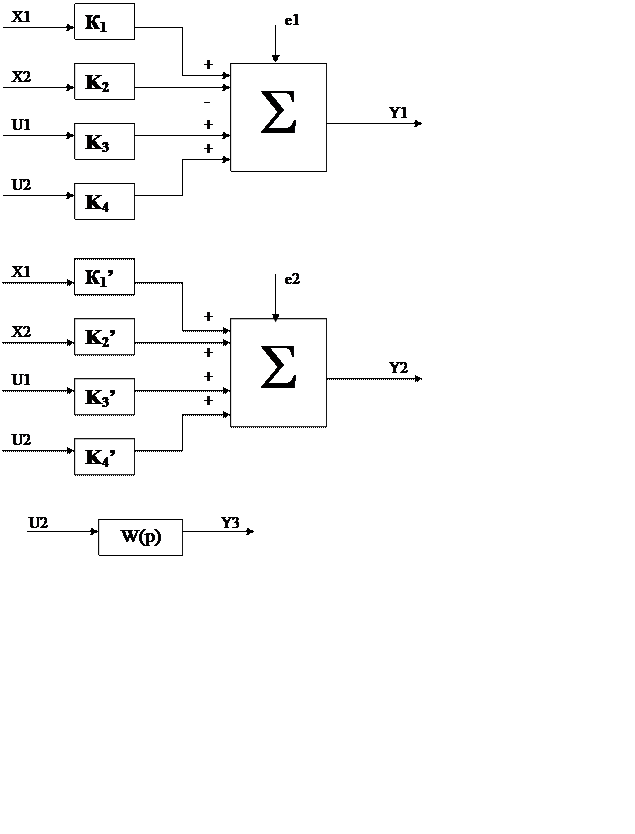Предпроектные НИР

В качестве критерия эффективности функционирования объекта, логичнее всего было бы выбрать Y2 (размер кристалла). Но так как диапазон изменения Y2 невелик, то для проведения исследований удобнее будет выбрать Y1(уровень раствора).

Информационный режим:

-  в условиях нормальной эксплуатации (KRISTALL.I14)

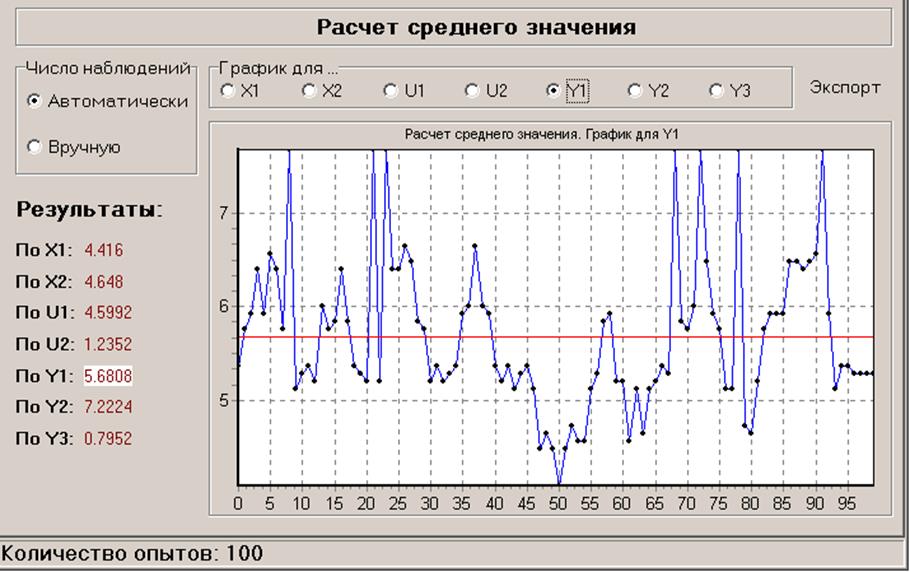
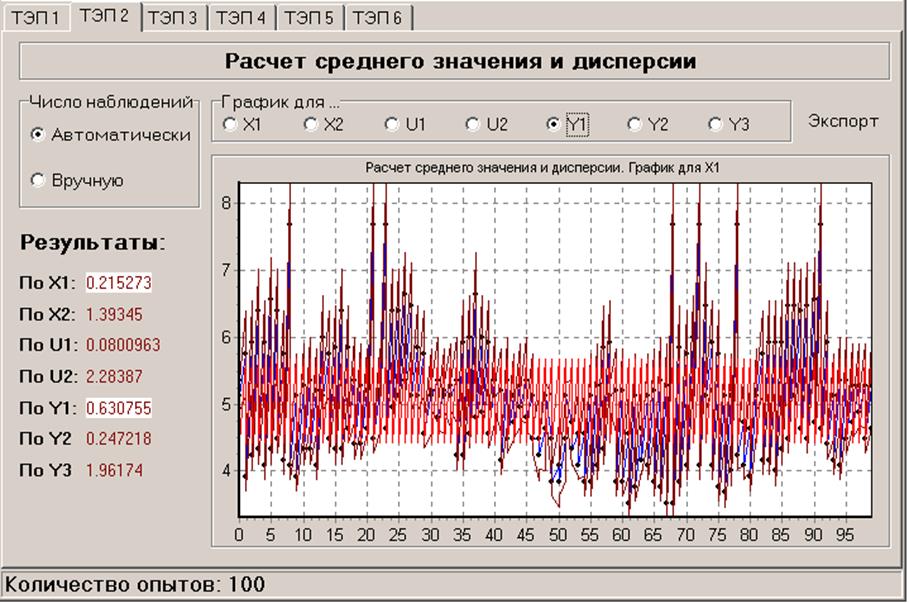
-  в режиме ручного управления (KRISTALL.I13)

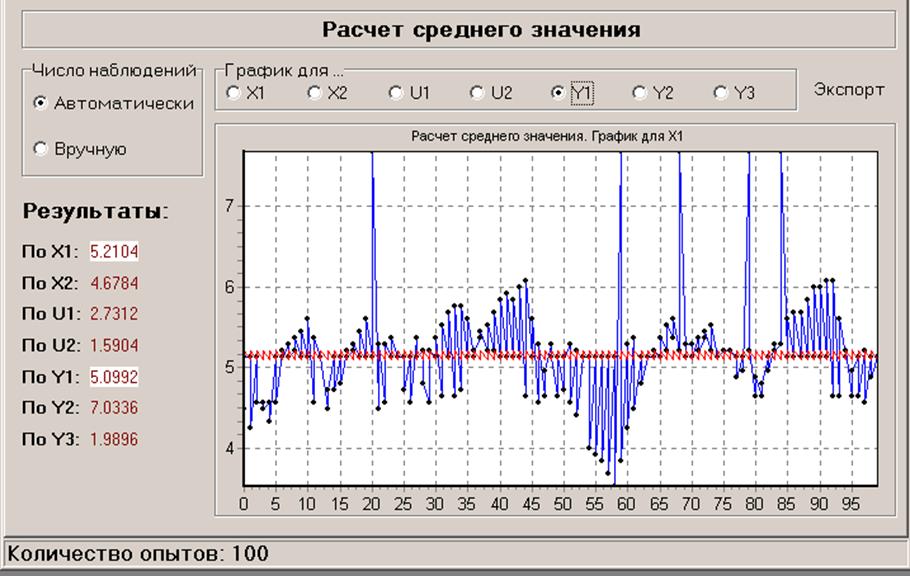
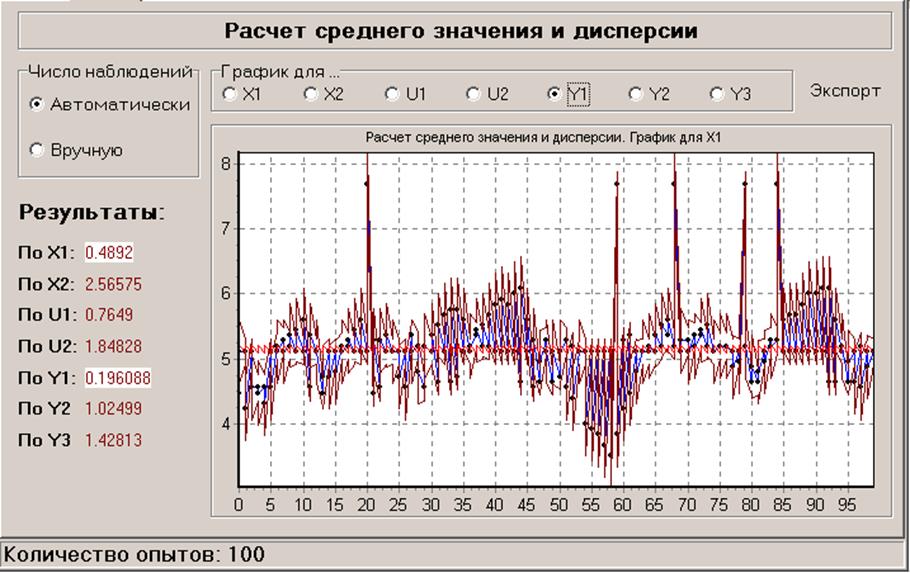
Из ТЭП2 (дисперсии) видно, что ручное управление оказалось более эффективным, в смысле меньшего разброса значений выходного параметра Y1 (выбранного в качестве критерия эффективности функционирования объекта).

Информационный режим (для оценивания интервалов корреляции) (KRISTALL.I15)

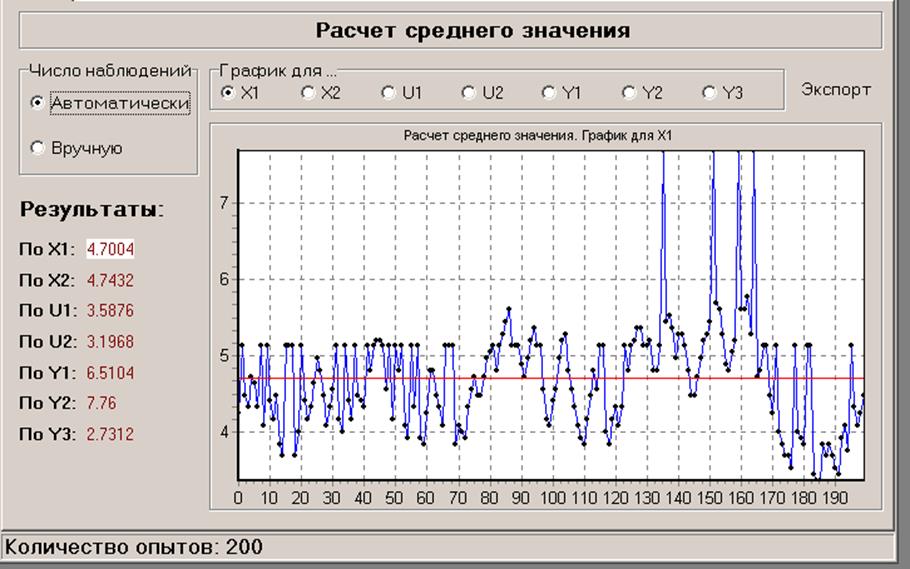
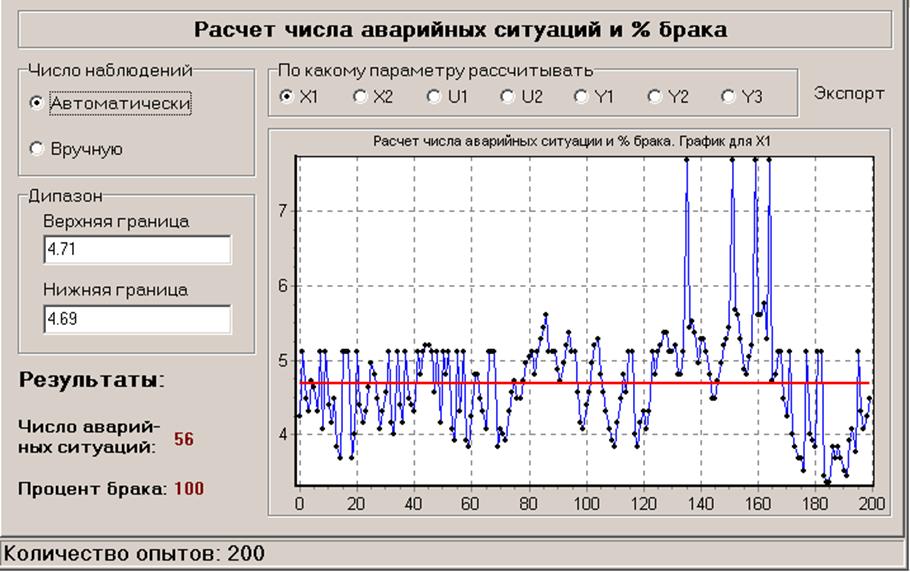
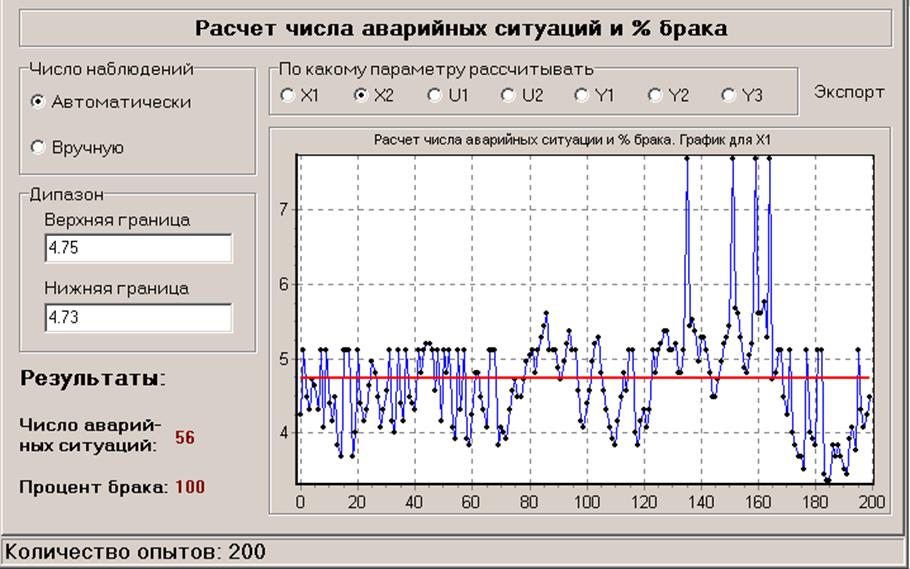
Интервал корреляции может быть грубо оценен через соотношение:

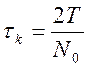
где N₀ – число пересечений реализацией x(t) за T время линии, соответствующей среднему значению процесса.

Для X1: N₀₁=56, 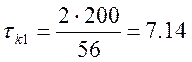c

Для X2: N₀₂=56, 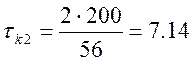c

, c Þ c

Уравнения авторегрессии для контролируемых неуправляемых переменных (x₁,x₂).

Теоретическая часть.

Обычно обнаруживается, что значения отклика в некоторой точке временного ряда сильно коррелированно с несколькими предшествующими и/или последующими значениями. Действительно, для многих явлений их современное состояние функционально определяется предшествующими состояниями системы, в большей степени недавними, в гораздо меньшей – далеко отстоящими от заданного по временному ряду. Подобные связи принято называть автокорреляцией – корреляцией ряда с самим собой.

Автокорреляция первого порядка характеризует связь между соседними значениями временного ряда, автокорреляция второго порядка – между отстоящими друг от друга на два периода и т.д. Вообще, автокорреляция n-го порядка относится к степени связанности откликов, разнесенных на n периодов. Предполагая, что возникшая связь между значениями сохранится некоторое время в будущем, мы получаем механизм прогнозирования, основанный на построении регрессии точек ряда на самих себя, то есть – авторегрессии.

Авторегрессионные модели разных порядков – первого, второго, в общем случае n-ого – можно описать уравнениями следующего вида:

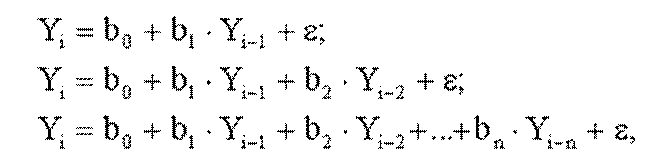
где b₀ - константа (свободный член) авторегрессионного уравнения, b₁, b₂,... b_n – коэффициенты авторегрессии, Y_i - величина отклика в некоторый момент времени, Y_i–1, Y_i–2,...Y_i–n – соответственно отклики одним, двумя,... n периодами ранее заданного, – случайная компонента, присутствующая в отклике и связанная с ошибками наблюдения и погрешностями модели.

Авторегрессионная модель позволяет спрогнозировать значения контролируемой неуправляемой переменной в следующий момент времени, что дает возможность с помощью изменения управляемых контролируемых переменных нейтрализовать негативное влияние изменения значения контролируемой неуправляемой переменной на значение отклика оптимизируемой переменной.

Эксперимент

Для построения авторегрессионных моделей проведем пассивный эксперимент на ОУ, при постоянном управляющем воздействии. Данные, полученные в ходе эксперимента, находятся в файле kristall.i2

Для анализа возьмем отрезки временных рядов такие, чтобы в них не было ошибочных откликов.

Данные для построения авторегрессионных моделей