Комбинационные устройства (автоматы без памяти)

Лекция 2

2.1 Комбинационные устройства

Комбинационные устройства (автоматы без памяти): их выходные сигналы однозначно определяются комбинациями входных сигналов в тот же момент времени.

При разработке логических схем рекомендуется следующая последовательность действий:

- словесное объяснение работы схемы с использованием логических высказываний;

- составление таблицы истинности на основе высказываний (формализации задачи);

- переход от табличного задания к алгебраическому выражению;

- упрощение (минимизация) алгебраического выражения;

- схемная реализация в заданной серии элементов (выбранном базисе).

Пример. Разработать схему подключения электродвигателя к рабочему и резервному источникам питания.

Словесное объяснение работы схемы:

При работе электродвигателя он может быть подключен или к рабочему, или к резервному питанию. Соединение указанных источников недопустимо, т. к. повреждение одного из них может вывести другой источник из строя.

Иначе: высказывание «электродвигатель работает (F)» истинно тогда и только тогда, когда истинно или «включено рабочее питание (X₁)» или «включено резервное питание (X₂)».

Составим таблицу истинности.

При двух переменных можно составить четыре различных набора. Для каждого набора заполним столбец F в соответствии с условиями задачи (таблица 2.1.1).

Таблица истинности                                                                                                 Таблица 2.1.1

№ набора	X2	X1	F	Все возможные режимы работы электродвигателя
0	0	0	0	Оба источника выключены, электродвигатель не работает
1	0	1	1	Электродвигатель работает от рабочего питания
2	1	0	1	Электродвигатель работает от резервного питания
3	1	1	0	Оба источника включать нельзя, электродвигатель не работает

Переход от табличного задания к алгебраическому выражению.

Составим логическую формулу из наборов дизъюнкций всех переменных, связанных конъюнкцией. Если переменные в таблице равны 1, то они входят в формулу в прямом виде, если равны 0 – то в инверсном. Выбираются наборы, для которых значение функции F равно логической 1 (используются наборы 1 и 2):

 

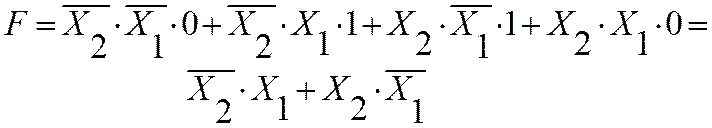Такая форма записи называется совершенной дизъюнктивной нормальной формой (СДНФ). Она позволяет считывать в аналитическом виде функции, представленные в табличной форме. С помощью нее можно сделать обратное преобразование в таблицу истинности, задавая значения переменных.

Любую сколь угодно сложную логическую функцию можно представить с помощью операций И, ИЛИ, НЕ в виде СДНФ. Однако, как и таблица истинности, эта форма громоздка и для ее сокращения используют методы минимизации.

Так же можно использовать инверсную запись СДНФ которая связана с прямой правилом Де Моргана. Выбираются наборы для нулевых значений функции, сама функция записывается как инверсная величина (используются наборы 0 и 3):

 

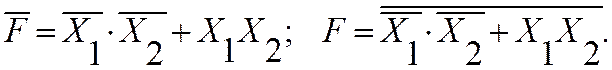С целью упрощения и реализации в заданном наборе элементов, для предложенной простой задачи, можно использовать известные преобразования:

 

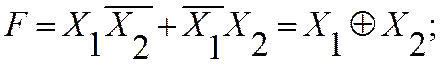Определение операции исключающее ИЛИ

(рис. 2.1.1):

 

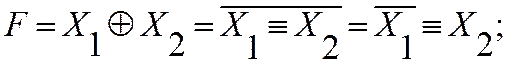Свойства данной операции:

Правило Де Моргана:

 

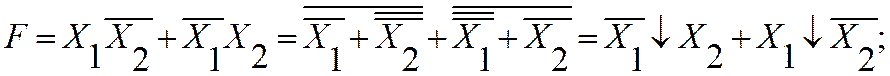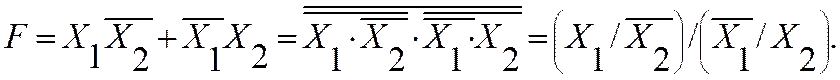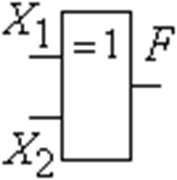
Рис.2.1.1 Возможная реализация схемы

Кроме СДНФ используют совершенную конъюнктивную нормальную форму (СКНФ). Она позволяет считывать в аналитическом виде функции, представленные в табличной форме.

Алгоритм нахождения СКНФ:

   - Выделяют наборы, где функция равна «0».

   - Составляют произведения наборов из сумм переменных, входящих в прямом виде, если переменная равна «0», в инверсном, если равна «1».

Для решаемой задачи СКНФ (используются нулевой и третий наборы):

 

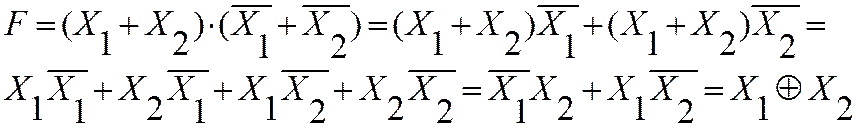Любую сколь угодно сложную логическую функцию можно представить с помощью операций И, ИЛИ, НЕ в виде СКНФ.

Если в таблице истинности значений функции равных единице больше, то для получения минимального выражения используют СКНФ или инверсную запись СДНФ, если больше нулей –  то СДНФ или инверсную запись СКНФ.

На следующем этапе используют правило склеивания, затем исключают выражения, которые не оказывают влияния на функцию (например, повторные выражения заменяют одним), если в результате получается несколько вариантов записи, то выбирается кратчайшая форма с учетом возможностей реализации на имеющихся цифровых микросхемах.

Например, в одном корпусе микросхемы может быть несколько однотипных элементов, часто четыре. Если для реализации схемы требуется пять однотипных элементов, то три штуки будут лишними, что нежелательно по условиям минимизации. Выход – использование другого выражения и иных микросхем.

Пример. Найти минимальную форму функции, заданной СДНФ:

 

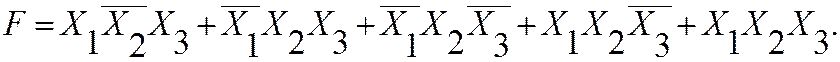Используя свойства:                                                                  и, добавив к функции:                                                  

 

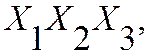получим:

 

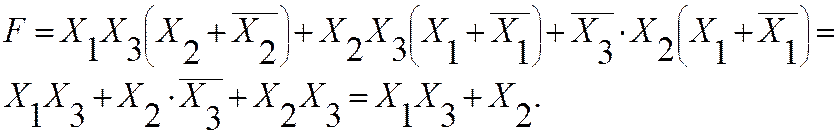Табличной формой данных преобразований в СДНФ является карта Карно.

2.1.1 Минимизация логических функций с помощью карт Карно

Карта Карно –  форма представления таблицы истинности. Правила построения карты:

   -  Количество клеток карты равно числу строк таблицы истинности.

   - Слева и сверху карты записываются символы переменных (инверсные значения не указываются).

   - В двух соседних клетках отличается значение только одной переменной (клетки на противоположных краях таблицы - соседние).

   - В клетки заносятся значения логической функции. Равные «1» объединяются в прямоугольники по 2ⁱ клеток. Все клетки, которые отличаются значением только одной переменной, являются соседними, несмотря на то, что иногда они расположены не рядом (для функций пяти переменных и более).

   - Для прямоугольников записывается произведение переменных, не изменяющих значения в соседних клетках.

   - Переменные в произведении указаны в прямом виде, если их значение в соседних клетках равны «1». Иначе – в инверсном.

   -  Произведения логически складываются  в искомую функцию.

 Разметка карты Карно, например,  для функции четырех переменных  (таблица 2.1.2):

Разметка карты Карно                                                                                              Таблица 2.1.2