1.3 Логические функции
Представление логических функций может быть словесное, табличное, алгебраическое, схемное, графическое и т.д.
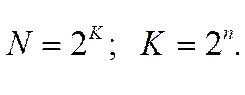 Функция F (X1, X2,…, X n) определена
на К = 2n наборах,
где n – число переменных. Для n переменных существует N различных логических функций:
Функция F (X1, X2,…, X n) определена
на К = 2n наборах,
где n – число переменных. Для n переменных существует N различных логических функций:
Все возможные логические функции одной переменной приведены в таблице 1.3.1.
Таблица истинности логических функций одной переменной Таблица 1.3.1
|
№ Набора |
Функция |
0 |
1 |
Обозначение |
Название |
|
0 |
|
0 |
0 |
0 |
Константа ноль |
|
1 |
|
0 |
1 |
|
Повторение |
|
2 |
|
1 |
0 |
Отрицание |
|
|
3 |
|
1 |
1 |
1 |
Константа единица |
Основные логические функции одной переменной.
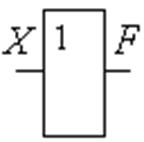
F2(X). Повторение истинного высказывания истинно, и наоборот.
Применяется как усилитель импульсных сигналов (рис. 1.3.1).
Рис. 1.3.1 Обозначение элемента повторения
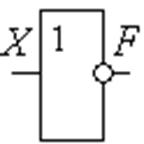
F3(X). Операция, соответствующая предлогу «не» - отрицание
(операция НЕ, инверсия). Отрицание истинного высказывания
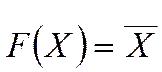 ложно,
и наоборот (читается: не Х , рис.1.3.2-1.3.4).
ложно,
и наоборот (читается: не Х , рис.1.3.2-1.3.4).
Рис. 1.3.2 Обозначение элемента отрицания
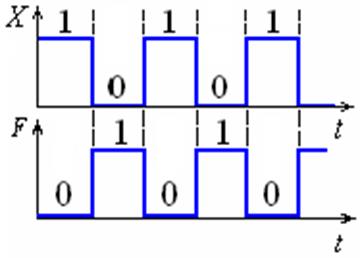
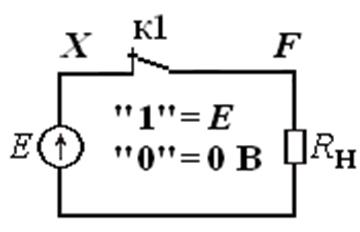
|
Рис. 1.3.3 Временные диаграммы операции НЕ |
Рис. 1.3.4 Реализация элемента НЕ на нормально замкнутом контакте реле К1. При включении реле (1) контакт размыкается (0), и наоборот |
Все возможные логические функции двух переменных F (X1, X2) приведены в таблице 1.3.2.
Таблица истинности логических функций двух переменных Таблица 1.3.2
|
X1 |
X2 |
F0 |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
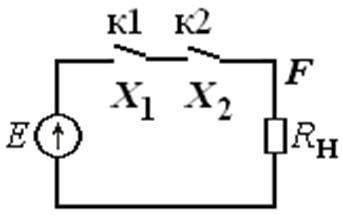
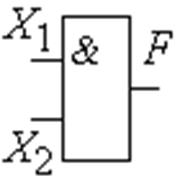
F1. Логическая связка, соответствующая союзу «и», называется конъюнкцией (операция И, логическое умножение). Она обозначается «/\», или « • », или «&», или «Ç», или знак опускается (рис.1.3.5-1.3.8).
Высказывание F = X1X2 истинно тогда и только тогда, когда истинны оба высказывания X1 и X2.
В общем случае: Функция F (X1, X2,…, X n) равна нулю, если равен нулю хотя бы один аргумент (равна единице, если равны единице все переменные).
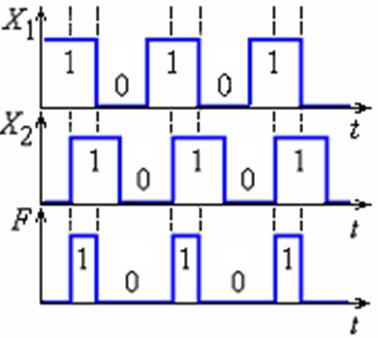
|
Рис. 1.3.5 Временные диаграммы операции И |
Рис. 1.3.6 Реализация операции И на нормально разомкнутых контактах К1 и К2 двух реле. При включении реле (1) контакт замыкается (1), и наоборот |
Рис. 1.3.7 Обозначение операции И. Элемент 2И, где 2 - число входов |
|
|
При подаче на оба входа сигналов логической единицы, равных +E, диоды VD1, VD2 закрыты. На выходе потенциал (рис. 1.3.8):
Если хотя бы на один вход подать нулевой потенциал земли, то соответствующий диод откроется и зашунтирует Rн. Это сопротивление станет много меньше R1 и U ≈ 0. |
F13. Логическая связка «если…, то…», называется импликацией. Обозначается «→».
Высказывание F = X1→X2 ложно тогда и только тогда, когда если X1 истинно, то X2 ложно.
Вопрос об истинности импликации решается при доказательстве теорем.
Действительно, всякая теорема имеет вид импликации, «из X1 следует X2», у которой в посылке (X1) стоит то, «что дано», а в заключении (X2) то, «что требуется доказать».
Пример. Высказывание X1: «Число 6 делится на 4».
Функция X1→X2: «Если заданное число делится на 4, то оно делится на 2».
Имеем: X1→X2 – истинная теорема. X2 – истинное высказывание.
Однако из этого нельзя делать вывод об истинности X1.
Иначе: из неверного утверждения верными методами можно получить верный результат. Но нельзя верными методами получить из верного утверждения неверный результат.
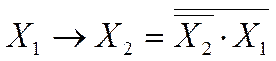 |
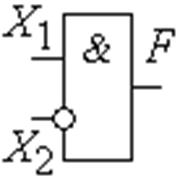 F2. Запрет по X2
(отрицание импликации).
F2. Запрет по X2
(отрицание импликации).
Обозначается «D». При равенстве запрещающей переменной
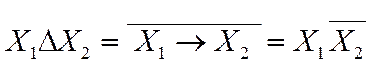 единице
функция равна нулю. Если запрещающая переменная
единице
функция равна нулю. Если запрещающая переменная
равна нулю, то функция принимает значение другой, информационной переменной (рис. 1.3.9):
|
Рис. 1.3.9 Обозначение операции запрет по X2. Элемент НЕТ |
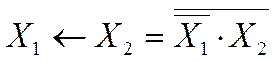 F11.
Импликация. Высказывание F =
X1←X2
ложно тогда и только тогда, когда если X2
истинно, то X1 ложно (рис.1.3.20).
F11.
Импликация. Высказывание F =
X1←X2
ложно тогда и только тогда, когда если X2
истинно, то X1 ложно (рис.1.3.20).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.