|
X3X4 X1X2 |
00 |
01 |
11 |
10 |
|
00 |
0000 |
0001 |
0011 |
0010 |
|
01 |
0100 |
0101 |
0111 |
0110 |
|
10 |
1100 |
1101 |
1111 |
1110 |
|
11 |
1000 |
1001 |
1011 |
1010 |
Разметка карты Карно (таблица 2.1.3) и таблица истинности (таблица 2.1.4) для рассматриваемого примера:
Разметка карты Карно Таблица 2.1.3 Таблица истинности Таблица 2.1.4
|
X2X3 X1 |
00 |
01 |
11 |
10 |
№ |
X1 |
X2 |
X3 |
F |
|
|
0 |
000 |
001 |
011 |
010 |
1 |
0 |
0 |
0 |
0 |
|
|
1 |
100 |
101 |
111 |
110 |
2 |
0 |
0 |
1 |
0 |
|
|
3 |
0 |
1 |
0 |
1 |
||||||
|
4 |
0 |
1 |
1 |
1 |
||||||
|
5 |
1 |
0 |
0 |
0 |
||||||
|
В карте запись в клетке, например, 001 соответствует набору в таблице истинности: |
6 |
1 |
0 |
1 |
1 |
|||||
|
7 |
1 |
1 |
0 |
1 |
||||||
|
8 |
1 |
1 |
1 |
1 |
||||||
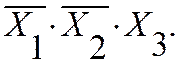
На основании таблицы истинности составим карту Карно (инверсные значения переменных в карте не указаны, таблица 2.1.5):
Карта Карно Таблица 2.1.5
|
|
|
||||
|
|
|
||||
|
|
0 |
0 |
1 |
1 |
|
|
|
0 |
1 |
1 |
1 |
|
Для прямой записи СДНФ: объединяем клетки, в которых функция равна «1» в два прямоугольника. В прямоугольнике А при переходе от одной клетки к другой не меняет свое значение на инверсное только переменная X2. В прямоугольнике Б только X2 изменяет свое значение.
Получим результат минимизации, эквивалентный приведенному выше:
 |
Для инверсной записи СДНФ:
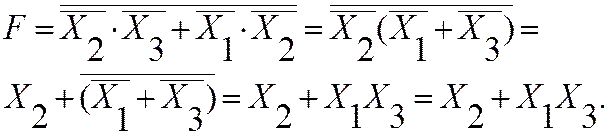 |
Для записи в СКНФ:
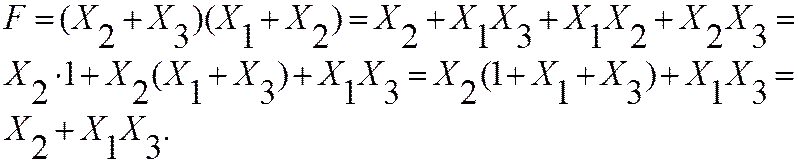 |
Общие правила минимизации с помощью карт Карно:
- одни и те же ячейки могут входить в состав разных контуров;
- число объединяемых ячеек одним контуром должно быть как можно больше;
- желательно, чтобы стороны контуров включали несколько ячеек.
Для возможности реализации полученного выражения в предпочтительном виде используются базисы.
2.1.2 Понятие базиса
Базис – набор логических функций, при помощи которых можно выразить любую другую логическую функцию.
Выражение одних логических функций через другие позволяет реализовывать логические выражения с помощью имеющихся технических средств или в предпочтительном виде с целью, например, минимизации затрат.
Доказательство, что набор логических функций является базисом – выражение с их помощью функций известного базиса ИЛИ, НЕ или аналогичного базиса И, НЕ.
Несколько базисов представлены в таблице 2.1.6.
Примеры базисов Таблица 2.1.6
|
Базисы |
|||
|
И, ИЛИ, НЕ |
ИЛИ – НЕ |
И – НЕ |
Сложение по модулю 2, И, константа 1 |
Пример: выразить в базисе «Сложение по модулю 2, И, константа 1» операции: ИЛИ, НЕ (операция И в составе базиса есть, таблица 2.1.7).
Реализация функций в базисе Таблица 2.1.7
|
Операция |
Аналитические преобразования |
Реализация |
|
ИЛИ |
|
|
|
НЕ |
|
|
Пример: выразить в базисе «ИЛИ – НЕ» операции: И, ИЛИ, НЕ (таблица 2.1.8).
Реализация функций в базисе Таблица 2.1.8
|
Операция |
Аналитические преобразования |
Реализация |
|
НЕ |
|
|
|
ИЛИ |
|
|
|
И |
|
|
Пример: выразить в базисе «И – НЕ» операции: И, ИЛИ, НЕ (таблица 2.1.9).
Реализация функций в базисе Таблица 2.1.9
|
Операция |
Аналитические преобразования |
Реализация |
|
НЕ |
|
|
|
И |
|
|
|
ИЛИ |
|
|
2.1.3 Равносильность логических функций
Доказательство равносильности осуществляется с помощью:
- Таблиц истинности.
- Правил алгебры логики.
- Приведением функций к СДНФ.
Пример. Пусть даны функции:
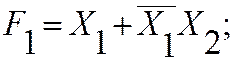 |
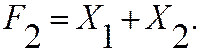 |
||
Доказать их равносильность всеми перечисленными способами.
Таблица истинности Таблица 2.1.10 Логические преобразования:
|
№ набора |
X1 |
X2 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
2 |
1 |
0 |
0 |
1 |
1 |
|
3 |
1 |
1 |
0 |
1 |
1 |
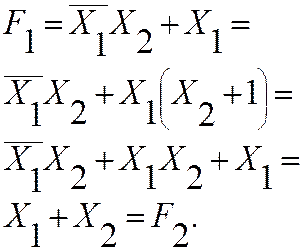
Функции на всех наборах равны
(таблица 2.1.10).
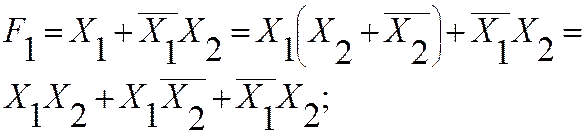 Приведение к СДНФ:
Приведение к СДНФ:
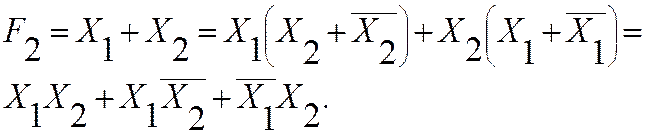 |
Следовательно, F1=F2.
2.1.3 Принцип двойственности
Две функции называются двойственными, если одна из другой получена взаимной заменой операций логических сложения и умножения. Или, если две функции равносильны, то равносильны их двойственные формы.
Принцип двойственности – инверсия логической суммы равна логическому произведению инверсий и наоборот (правило Де Моргана частный случай этого принципа).
Пример: для равносильных функций вышеприведенного примера доказать равносильность их двойственных форм.
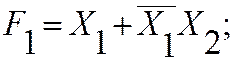 |
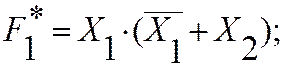 |
||
двойственная форма:
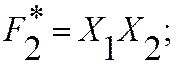
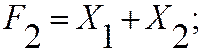
двойственная форма:
где произведена взаимная замена логических операций.
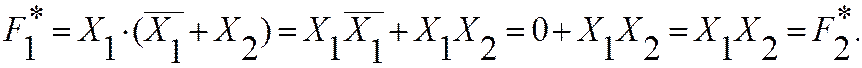 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.