ЛАБОРАТОРНАЯ РАБОТА № 2
ПЕРВИЧНЫЕ И ВОЛНОВЫЕ ПАРАМЕТРЫ ВЛ
1. Для ВЛ, выполненной на опорах заданного типа и класса напряжения, определить требуемые для расчета первичных и волновых параметров среднегеометрические размеры.
2. Рассчитать аналитически емкости, индуктивности, волновые сопротивления и скорости распространения волны для прямой и нулевой последовательностей фаз в трехфазной ВЛ без потерь.
3. С помощью программы для расчета параметров многопроводной ВЛ PARAMETR рассчитать фазные и междуфазные первичные параметры линии с потерями:
- для трехфазной ВЛ без тросов f =50 Гц и rз = 100 Ом×м;
- для трехфазной ВЛ с тросами f =50 Гц и rз = 100 Ом×м;
- для трехфазной ВЛ без тросов f =50 кГц и rз = 100 Ом×м;
- для трехфазной ВЛ без тросов f =50 Гц и rз = 1000 Ом×м.
4. По полученным в разделе 3 первичным параметрам ВЛ, рассчитать емкости, индуктивности, волновые сопротивления и скорости распространения волны для прямой и нулевой последовательностей фаз для всех рассмотренных случаев.
5. Составить отчет, который должен содержать:
- исходные данные;
- геометрию расположения проводов;
- результаты расчетов параметров ВЛ;
- таблицу, позволяющую проанализировать влияние различных факторов на параметры ВЛ;
- анализ полученных результатов.
При распространении волны по одному из проводов трехфазной линии на других проводах за счет электромагнитной связи также возникают волны. Волновые уравнения трехпроводной электромагнитно связанной системы записываются в виде:
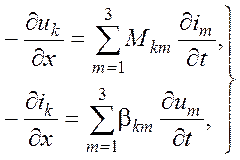 (1)
(1)
где
![]() - собственные и взаимные коэффициенты
электростатической индукции,
- собственные и взаимные коэффициенты
электростатической индукции,
![]() - коэффициент взаимной индукции между петлями k-тый
провод-земля и m-тый провод-земля, Mkk=Lkk – коэффициент
самоиндукции петли k-тый провод-земля, которые определяются из выражений:
- коэффициент взаимной индукции между петлями k-тый
провод-земля и m-тый провод-земля, Mkk=Lkk – коэффициент
самоиндукции петли k-тый провод-земля, которые определяются из выражений:
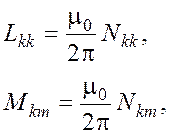
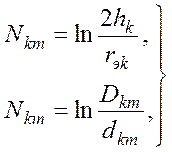 (2)
(2)
где hk , Dkm и dkm - поперечные габариты (рис.1), rэk - эквивалентный радиус расщепленного на n составляющих провода, который определяется по формуле:
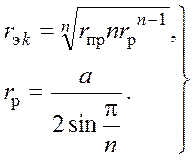 (3)
(3)
( rпр.- радиус составляющей фазы, a – расстояние между составляющими фазы).
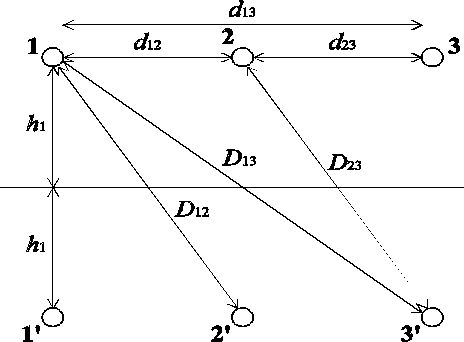
Рис.1. К определению первичных параметров трехфазной ВЛ
Коэффициенты электростатической индукции b определяются из решения системы уравнений Максвелла
U= a×Q (4)
где U и Q - матрицы-столбцы напряжений и зарядов на проводах; a - квадратная матрица потенциальных коэффициентов, определяемых как
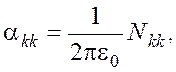
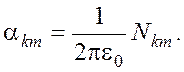
Решение матричного уравнения (4) относительно зарядов позволяет получить матрицу b:
Q = a-1×U = b×U . (5)
Для решения практических задач часто необходимо определить первичные и волновые параметры идеально транспонированной трехфазной линии, то есть линии с условно одинаковым расположением проводов относительно друг друга и земли. В такой линии будут выполняться условия:
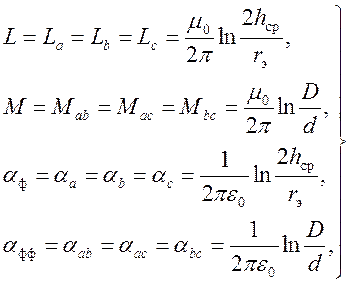 (6)
(6)
где
![]() - среднегеометрическая высота
подвеса проводов над землей,
- среднегеометрическая высота
подвеса проводов над землей,
![]() - среднегеометрические расстояния между проводом и
зеркальными (относительно плоскости земли) изображениями проводов других фаз,
- среднегеометрические расстояния между проводом и
зеркальными (относительно плоскости земли) изображениями проводов других фаз,
![]() -
среднегеометрическое расстояние между проводами фаз.
-
среднегеометрическое расстояние между проводами фаз.
Для определения первичных емкостных параметров ВЛ для прямой и нулевой последовательностей фаз запишем уравнения, связывающие мгновенные значения напряжений с мгновенными значениями зарядов на фазах (расположение векторов зарядов для прямой и нулевой последовательностей приведено на рис.2.)
![]()
![]()
![]()
![]() .
.
qc1 ![]()

![]()
 -0,5qa qa1
qa0
-0,5qa qa1
qa0
![]()
![]()
![]() qb0
qb0
![]() qc0
qc0
а) б)
qb1
Рис. 2. К определению параметров ВЛ для прямой (а) и нулевой (б)
последовательностей фаз
Таким образом для идеально транспонированной ВЛ емкость прямой последовательности будет равна
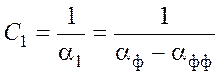 . (7)
. (7)
Аналогично получим емкость нулевой последовательности:
![]()
![]() ,
,
![]()
![]()
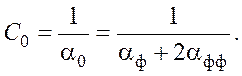 (8)
(8)
Для определения индуктивных параметров ВЛ для прямой и нулевой последовательностей фаз запишем уравнения, связывающие мгновенные значения потокосцепления с мгновенными значениями токов в фазах:
![]()
![]()
![]()
![]()
Таким образом для идеально транспонированной ВЛ индуктивность для прямой последовательностей фаз будет равна
![]() .
(9)
.
(9)
Аналогично получим индуктивность для нулевой последовательностей фаз:
![]()
![]()
![]()
![]()
![]() .
(10)
.
(10)
Линии электропередачи 110 кВ и выше с целью симметрирования параметров выполняются с транспозицией проводов. Для таких линий фазные и междуфазные индуктивные и емкостные параметры рассчитываются по выражениям (2) - (5) или по программе PARAMETR как для не транспонированной линии. При этом параметры ВЛ для прямой и нулевой последовательностей фаз, можно получить через усредненные параметры
![]()
![]()
![]() ,
,
![]() ,
,
следующим образом: индуктивности - по выражениям (9) и (10),
а емкости для прямой и нулевой последовательностей фаз как ![]() и
и ![]() .
.
Расчет параметров воздушных линий электропередачи проводится на ПЭВМ с помощью специально разработанной программы PARAMETR, предназначенной для расчетов параметров многопроводной ВЛ с учетом потерь в земле.
Исходными данными для расчетов являются геометрия расположения проводов и тросов в пролете ВЛ, конструкция фазы и троса, удельное сопротивление грунта, удельные активные сопротивление проводов и тросов и частота процессов, для которых определяются параметры. Пример задания исходных данных приведен на рис.3.
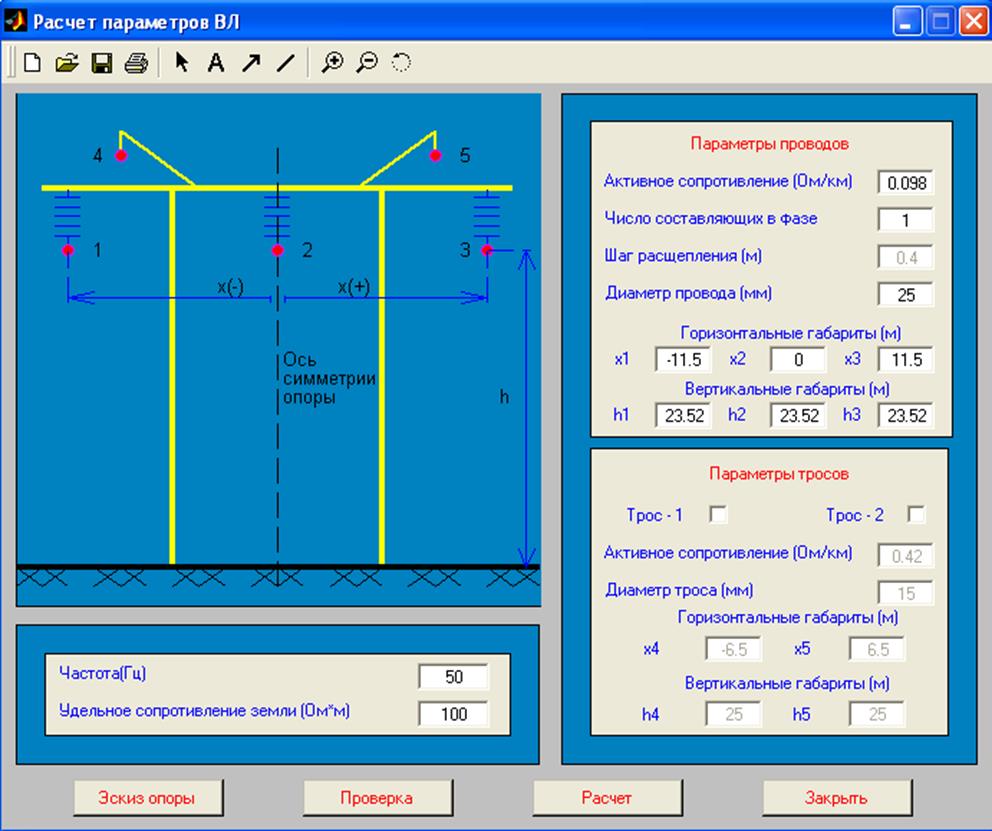
Рис.3 Пример задания исходных данных для расчета первичных
параметров одноцепной ВЛ с тросом при частоте f=50 Гц и rз=100 Ом×м
![]()
В результате расчета выдаются матрицы погонных активных, индуктивных и емкостных параметров ВЛ с учетом активного сопротивления земли и проводов. Пример выдачи результатов расчета параметров четырехпроводной ВЛ (три фазы и грозозащитный трос) приведен на рис.4.
Результаты расчетов
------------------------------Частота (Гц)----------------------------------
f =50
-----------------------Сопротивление земли (Ом*м)---------------------------
R_z = 100
-----------------Матрица продольных сопротивлений (Ом/км)-------------------
R =
1.4735e-001 4.9350e-002 4.9350e-002
4.9350e-002 1.4735e-001 4.9350e-002
4.9350e-002 4.9350e-002 1.4735e-001
----------------------Матрица индуктивностей (Гн/км) ------------------------
L =
2.2555e-003 8.9071e-004 7.5285e-004
8.9071e-004 2.2555e-003 8.9071e-004
7.5285e-004 8.9071e-004 2.2555e-003
------------Матрица коэффициентов электростатической индукции(Ф/км) ---------
beta =
7.0024e-009 -1.1352e-009 -5.0148e-010
-1.1352e-009 7.1505e-009 -1.1352e-009
-5.0148e-010 -1.1352e-009 7.0024e-009
------------------------Матрица фазных емкостей (Ф/км) ----------------------
C =
5.3657e-009 1.1352e-009 5.0148e-010
1.1352e-009 4.8801e-009 1.1352e-009
5.0148e-010 1.1352e-009 5.3657e-009
Рис.4. Пример выдачи результатов расчета первичных параметров ВЛ
1. Что характеризует активное продольное сопротивление и волновое сопротивление ВЛ?
2. Как изменятся и почему первичные и волновые параметры трехфазной ВЛ при их определении на промышленной частоте (50 Гц) и на частоте грозовых перенапряжений (50 кГц)?
3. Как влияет на первичные и волновые параметры для прямой и нулевой последовательностей фаз удельное сопротивление грунта?
4. На какие первичные параметры оказывают влияние частота исследуемого процесса и удельное сопротивления грунта?
5. На какие первичные и волновые параметры ВЛ влияет наличие грозозащитного троса?
6. Для чего необходимо определять параметры для прямой и нулевой последовательностям фаз?
7. Следует ли учитывать потери в земле при определении параметров ВЛ для прямой последовательности фаз ?
8. При исследовании каких режимов используются параметры прямой и нулевой последовательностей фаз?
ЛИТЕРАТУРА
1. К.П. Кадомская. – Перенапряжения в энергосистемах/ Часть I. Волновые процессы в ВЛ и КЛ.- НЭТИ, Новосибирск.-1980, 100 с.
2. Справочник по электрическим установкам высокого напряженния/ Под ред. И.А. Баумштейна и М.В. Хомякова.- 2-0е изд., перераб. и доп..- М.: Энергоиздат, 1981.- 656 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.