


L. 330. «Электротехника» Аксютин В.А.
Элементы линейной цепи гармонического тока: источники, резистор, индуктивность и взаимной индуктивность, ёмкость
1. Источники ЭДС и тока
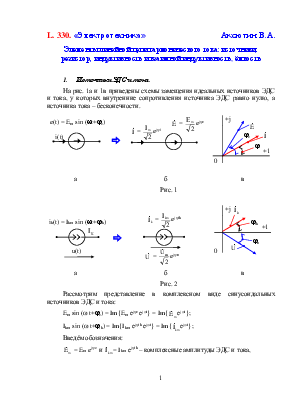
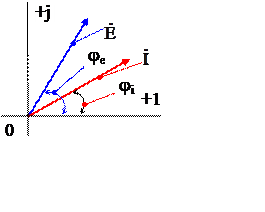
На рис. 1а и 1в приведены схемы замещения идеальных источников ЭДС и тока, у которых внутренние сопротивления источника ЭДС равно нулю, а источника тока – бесконечности.
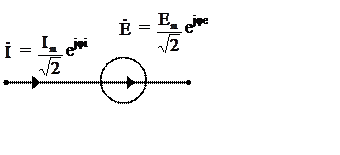 |
|||||
 |
|||||
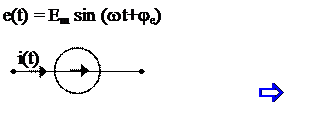 |
|||||
а б в
Рис. 1
 |
|||||
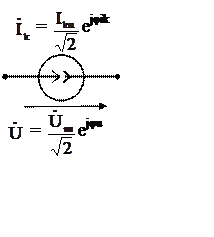 |
|||||
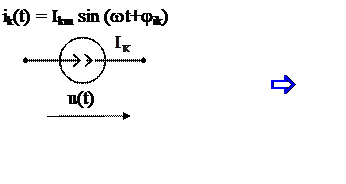 |
|||||
а б в
Рис. 2
Рассмотрим представление в комплексном виде синусоидальных источников ЭДС и тока:
Em
sin (ω t+je) = Im{Em еjje еjωt} = Im{![]() еjωt};
еjωt};
Ikm sin (ω t+jik) = Im{Ikm еjjik еjωt} = Im{![]() еjωt};
еjωt};
Введём обозначения:
![]() =
Em ejje и
=
Em ejje и ![]() = Ikm еjjik – комплексные амплитуды ЭДС и тока,
= Ikm еjjik – комплексные амплитуды ЭДС и тока,
![]() =
=
![]() =
= ![]() ejje ,
ejje , ![]() =
= ![]() =
= ![]() ejjik - комплексы действующих
значений ЭДС и тока.
ejjik - комплексы действующих
значений ЭДС и тока.
Для расчёта установившихся режимов цепи с синусоидальными источниками применяются схемы замещения цепи в комплексном виде, где каждый элемент имеет своё обозначение и параметры. Обозначения источников ЭДС и тока в комплексном виде приведено на рис 1б и 1г.
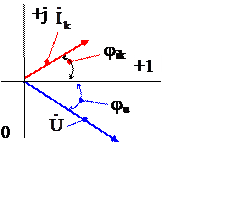
Полученные соотношения позволяют построить ВД: рис. 1,в для источника ЭДС; рис. 2.в для источника тока.
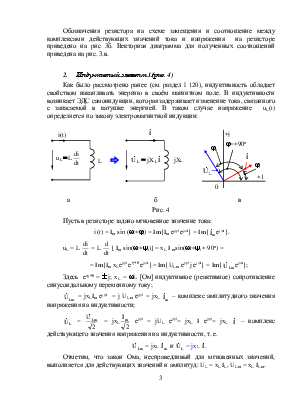
2. Резистивный элемент R (рис. 3)
Пусть в резисторе задано мгновенное значение тока
i (t) = Im sin (wt+ji) = Im{Im еjji еjωt} = Im{![]() еjωt},
еjωt},
где ![]() = Im еjji – комплекс амплитудного значения тока,
= Im еjji – комплекс амплитудного значения тока,
![]() =
= ![]() = I еjji – комплекс действующего значения тока.
= I еjji – комплекс действующего значения тока.
 |
|||||||
 |
|||||||
 |
|||||||
|
|||||||
а б в
Рис. 3
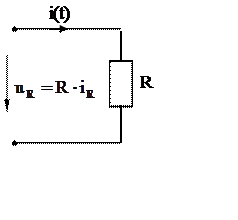
Связь между током и напряжением в любой момент времени на резисторе подчиняется закону Ома. Природа сопротивления R протеканию электрического тока такова, что оно не вызывает сдвига по фазе между током и напряжением. Поэтому:
uR(t) = R Im sin (wt+ji) = URm
sin (wt+ji) = Im{URm еjji еjωt} = Im{![]() еjωt};
еjωt};
![]() = URm
еjji – комплекс
амплитудного значения напряжения на резисторе.
= URm
еjji – комплекс
амплитудного значения напряжения на резисторе.
![]() =
= 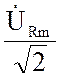 =
= 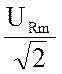 еjji = UR еjji= R I еjji= R
еjji = UR еjji= R I еjji= R ![]() – комплекс действующего
значения напряжения на резисторе, т. е.
– комплекс действующего
значения напряжения на резисторе, т. е. ![]() = R
= R ![]() .
.
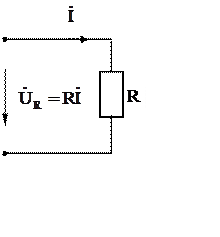
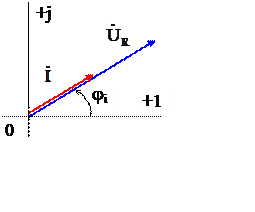
Обозначения резистора на схеме замещения и соотношение между комплексами действующих значений тока и напряжения на резисторе приведено на рис 3б. Векторная диаграмма для полученных соотношений приведена на рис. 3.в.
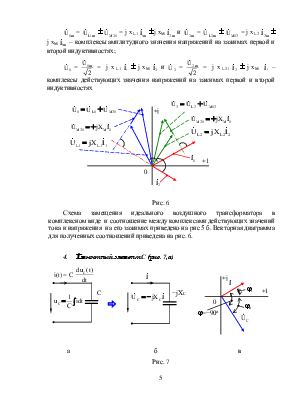
2. Индуктивный элемент L(рис. 4)
Как было рассмотрено ранее (см. раздел l 120), индуктивность обладает свойством накапливать энергию в своём магнитном поле. В индуктивности возникает ЭДС самоиндукции, которая задерживает изменение тока, связанного с запасаемой в катушке энергией. В таком случае напряжение uL(t) определяется по закону электромагнитной индукции:
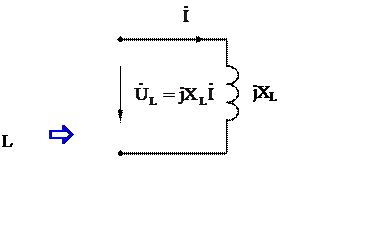 |
|||||
 |
|||||
 |
|||||
а б в
Рис. 4
Пусть в резисторе задано мгновенное значение тока:
i (t) = Im sin (wt+ji) = Im{Im еjji еjωt} = Im{![]() еjωt}.
еjωt}.
uL = L ![]() = L
= L ![]() [ Im sin(wt+yi)] = xL I msin(wt+yi + 90o) =
[ Im sin(wt+yi)] = xL I msin(wt+yi + 90o) =
= Im{Im xLеjji е+j90 еjωt }=
Im{ULm еjji j еjωt} = Im{![]() еjωt};
еjωt};
Здесь е±j90 = ± j; xL = wL [Ом] индуктивное (реактивное)сопротивление синусоидальному переменному току;
![]() = jxLIm еjji = j ULm
еjji = jxL
= jxLIm еjji = j ULm
еjji = jxL ![]() – комплекс амплитудного
значения напряжения на индуктивности;
– комплекс амплитудного
значения напряжения на индуктивности;
![]() =
= 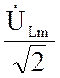 = jxL
= jxL![]() еjji = jUL еjji= jxL I еjji= jxL
еjji = jUL еjji= jxL I еjji= jxL ![]() – комплекс действующего
значения напряжения на индуктивности, т. е.
– комплекс действующего
значения напряжения на индуктивности, т. е.
![]() =
jxL
=
jxL ![]() и
и ![]() = jxL
= jxL ![]() .
.
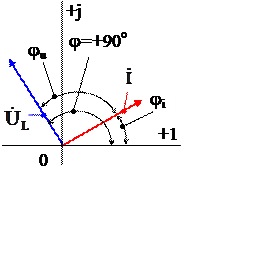
Отметим, что закон Ома, несправедливый для мгновенных значений, выполняется для действующих значений и амплитуд: UL = xL IL, ULm = xL ILm.
Из полученных соотношений видно, что по фазе напряжение на индуктивности опережает ток на +90о: yu= yi + 90o.
Обозначения индуктивного сопротивления на схеме замещения и соотношение между комплексами действующих значений тока и напряжения на индуктивности приведено на рис 4б. Векторная диаграмма для полученных соотношений приведена на рис. 4.в.
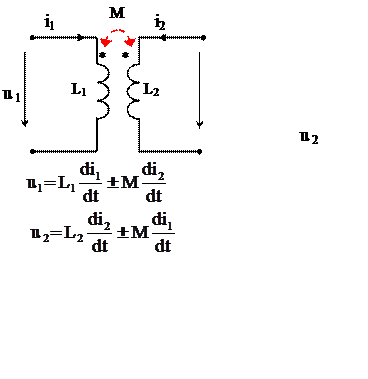
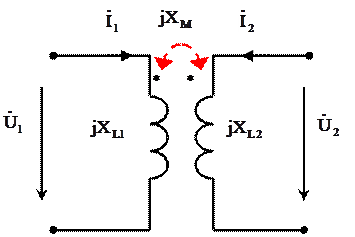
3. Взаимная индуктивность (рис. 5,а)
Пусть в идеальном трансформаторе (рис. 5,а) установившийся режим синусоидального тока. Токи в катушках:
i1(t) = Im1 sin(ω t + φ1) и i2(t) = Im2 sin(ω t + φ2).
 |
|||||||||
 |
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
а б
Рис. 5
Напряжения на зажимах первой и второй катушек (см. раздел l 120):
u1
= L1![]() ±M
±M![]() = xL1 Im1 sin(wt+j1+90o) ± xM Im2 sin(wt+j2+90o) =
= xL1 Im1 sin(wt+j1+90o) ± xM Im2 sin(wt+j2+90o) =
Im{I1m xL1еjj1 е+j90 еjωt}± Im{I2M xMеjj2 е+j90 еjωt} =
Im{(j
x L1 ![]() ± j xM
± j xM ![]() ) еjωt} = Im{(
) еjωt} = Im{(![]() ±
± ![]() ) еjωt}
) еjωt}
u2=L2![]() ±M
±M![]() =xL2 Im2 sin(wt+j2+90o) ± xM Im1 sin(wt+j1+90o) =
=xL2 Im2 sin(wt+j2+90o) ± xM Im1 sin(wt+j1+90o) =
Im{I2m xL2еjj2 е+j90 еjωt} ± Im{I1M xMеjj1 е+j90 еjωt} =
Im{(j
x L2 ![]() ± j xM
± j xM ![]() ) еjωt} = Im{(
) еjωt} = Im{(![]() ±
± ![]() ) еjωt}
) еjωt}
где: xL1 = ωL1, xL2 = ωL2 и xM = ωM - индуктивные сопротивления, катушек L1 и L2 и сопротивление взаимной индуктивности между катушками, размерность Ом.
![]() =
= ![]() ±
± ![]() = j x L1
= j x L1 ![]() ± j xM
± j xM ![]() и
и ![]() =
=
![]() ±
± ![]() = j x L2
= j x L2 ![]() ± j xM
± j xM ![]() – комплексы амплитудного
значения напряжений на зажимах первой и второй индуктивностях;
– комплексы амплитудного
значения напряжений на зажимах первой и второй индуктивностях;
![]() =
= 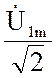 = j x L1
= j x L1 ![]() ± j xM
± j xM ![]() и
и ![]() =
=
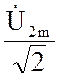 = j x L21
= j x L21 ![]() ± j xM
± j xM ![]() – комплексы
действующих значения напряжений на зажимах первой и второй индуктивностях
– комплексы
действующих значения напряжений на зажимах первой и второй индуктивностях
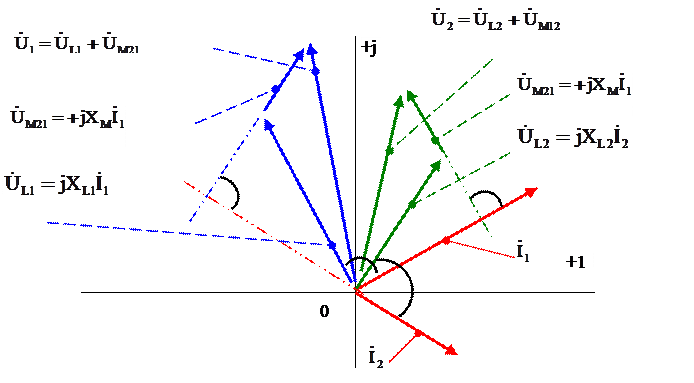 |
Рис. 6
Схема замещения идеального воздушного трансформатора в комплексном виде и соотношение между комплексами действующих значений тока и напряжения на его зажимах приведено на рис 5 б. Векторная диаграмма для полученных соотношений приведена на рис. 6.
4. Ёмкостный элемент C (рис. 7,а)
 |
|||||
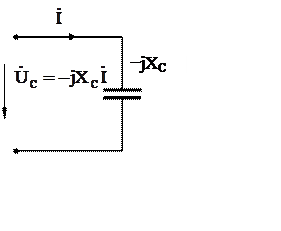 |
|||||
 |
|||||
а б в
Рис. 7
Как было рассмотрено ранее (см. раздел l 120), ёмкость обладает свойством накапливать электрические заряды и, следовательно, запасать энергию в электрическом поле. Пусть к ёмкости подключён источник синусоидального напряжения:
uС(t) =UCm sin(wt+ φ u).
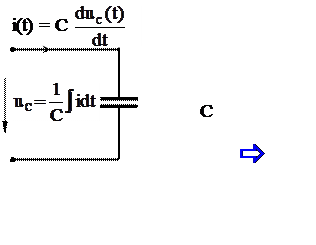
Выражение для тока найдём как изменение заряда ёмкости во времени. Будем считать напряжение заданным:
i(t)= ![]() = C
= C 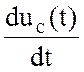 = C wUCm cos(wt+ φu) =
= C wUCm cos(wt+ φu) = ![]() UCm
sin(wt+ φu + 90o) =
UCm
sin(wt+ φu + 90o) =
Im sin(wt+φi) = Im{UCm ![]() еjju
е+j90 еjωt }= Im{Im еjji
j еjωt} = Im{
еjju
е+j90 еjωt }= Im{Im еjji
j еjωt} = Im{![]() еjωt};
еjωt};
Здесь: е+j90 = + j; 1/j = -j;
xС = 1/wC [Ом] ёмкостное (реактивное)сопротивление синусоидальному переменному току;
![]() =
=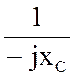 Um еjju =
Um еjju = 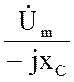 =
= 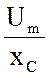 еjji = Im
еjji – комплекс
амплитудного значения тока на ёмкости;
еjji = Im
еjji – комплекс
амплитудного значения тока на ёмкости;
![]() =
= 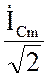 =
= 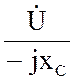 –
комплекс действующего значения тока через ёмкость.
–
комплекс действующего значения тока через ёмкость.
Интерес представляет выражения для комплексных амплитуд и действующих напряжений на ёмкости:
![]() =
−j xС
=
−j xС![]() и
и ![]() =
− j xС
=
− j xС ![]() .
.
Отметим, что закон Ома, несправедливый для мгновенных значений, выполняется для действующих значений и амплитуд: UС = xС I, UСm = xС Im.
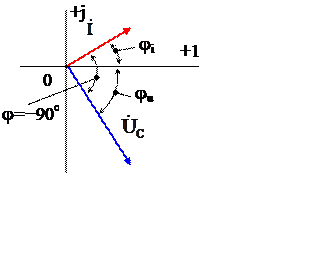
Из полученных соотношений видно, что ток через ёмкость опережает напряжение по фазе на угол +90о: φi= φu + 90o.
Обозначения ёмкостного сопротивления на схеме замещения и соотношение между комплексами действующих значений тока и напряжения на ёмкости приведено на рис 7б. Векторная диаграмма для полученных соотношений приведена на рис. 7.в.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.