

L. 393. «Электротехника» Аксютин В.А.
Экспериментальное определение коэффициентов четырёхполюсника А11, А12, А21, А22
Для определения коэффициентов четырёхполюсника можно использовать результаты любых трёх опытов из следующих четырёх:
1. прямой холостой ход (ХХ);
2. прямое короткое замыкание (КЗ),
3. обратный ХХ;
4. обратное КЗ.
Для симметричного четырёхполюсника достаточно первых двух опытов. Получим формулы для определения коэффициентов по результатам 1, 2 и 4 опытов.
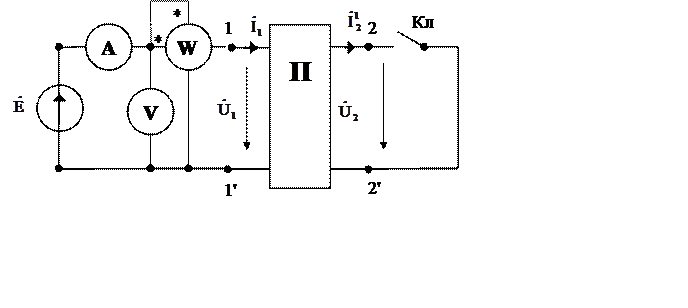 |
Рис. 1
1. Прямой ХХ четырёхполюсника (рис. 1, Кл. разомкнут).
ZH= ¥, поэтому ![]() = 0.
= 0.
Уравнения типа «А» четырехполюсника:
![]()
![]() = A11
= A11![]() + A12
+ A12 ![]() , (1)
, (1)
![]() = A12
= A12![]() + A22
+ A22 ![]() , (2)
, (2)
Тогда уравнения (1) и (2) принимают вид:
![]()
![]() 1X = A11
1X = A11 ![]() 2X,
2X,
![]() 1X = A21
1X = A21 ![]() 2X.
2X.
Таким образом:
A11 = ![]() 1X /
1X /![]() 2X, (3)
2X, (3)
A21 = ![]() 1X /
1X /![]() 2X . (4)
2X . (4)
Согласно (3) и (4) находятся A11 и A21 только у четырёхполюсника постоянного тока. Для четырёхполюсника переменного тока приборы показывают только лишь модули комплексов действующих значений напряжения и тока, а не сами комплексы. Поэтому в опыте ХХ по показаниям трёх приборов (амперметра, вольтметра и ваттметра) находят комплекс входного сопротивления Z1X, а его связь с коэффициентами:
Z1X = 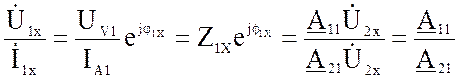 ; Z1X =
; Z1X = 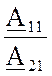 (5)
(5)
где UV1, IA1 и PW1- показания вольтметра, амперметра и ваттметра в режиме прямого ХХ,
Z1X = 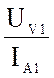 и
j1Х =
и
j1Х = 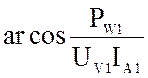 модуль и аргумент входного
сопротивления
модуль и аргумент входного
сопротивления
2. Прямое КЗчетырёхполюсника (рис. 1, Кл. замкнут).
Z2 = 0 и ![]() 2 = 0.
2 = 0.
Тогда уравнения (1) и (2) принимают вид:
![]()
![]() 1к = A12
1к = A12 ![]() к,
к,
![]() 1к = A22
1к = A22 ![]() к,
к,
откуда
![]() A12 =
A12 = ![]() 1к /
1к / ![]() к; (6)
к; (6)
A22 = ![]() 1к/
1к/ ![]() к. (7)
к. (7)
По (5) и (7) находятся коэффициенты четырёхполюсника постоянного тока. Таким образом, для четырёхполюсника постоянного тока достаточно двух опытов, чтобы получить систему формул (1) и (2). Для четырёхполюсника переменного тока по проведенному опыту определяется Z1K, а его связь с коэффициентами:
Z1K = 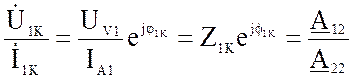 или
Z1K =
или
Z1K = 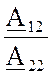 (8)
(8)
UV1, IA1 и PW1- показания приборов в режиме прямого КЗ,
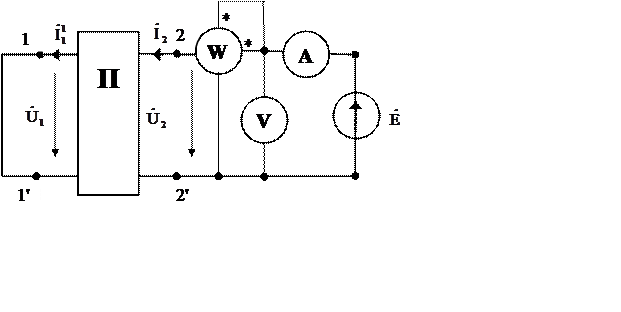 |
Рис. 2
Z1K = 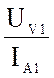 и
j1K =
и
j1K = 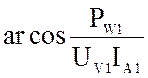 модуль и
аргумент входного сопротивления в режиме прямого КЗ
модуль и
аргумент входного сопротивления в режиме прямого КЗ
3. Обратное КЗ четырёхполюсника(рис. 2).
Система уравнений четырёхполюсника при его питании со стороны выходных зажимов:
![]()
![]() 1
= A11
1
= A11 ![]() 2 + A12(−
2 + A12(−![]() 2), (7)
2), (7)
−![]() = A21
= A21 ![]() 2 + A22 (−
2 + A22 (−![]() 2). (8)
2). (8)
Выражая ![]() 2 и
2 и ![]() 2
через
2
через ![]() 1 и
1 и ![]() , в (7) и (8) получим:
, в (7) и (8) получим:
![]()
![]() 2 = A22
2 = A22 ![]() 1 + A12
1 + A12 ![]() ,
,
![]() 2 = A21
2 = A21 ![]() 1 + A11
1 + A11 ![]() .
.
При обратном КЗ:
![]() 1 = 0 и
1 = 0 и ![]() 2K = A12
2K = A12 ![]() K I2к = A11
K I2к = A11![]() K.
K.
Таким образом,
Z2K = 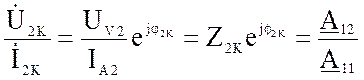 ; откуда Z2K =
; откуда Z2K = ![]() . (9)
. (9)
В (9) UV2, IA2 и PW2- показания приборов в режиме обратного КЗ,
Z2K = 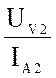 и j2K =
и j2K = 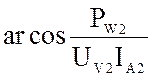 модуль и аргумент входного
сопротивления в режиме обратного КЗ
модуль и аргумент входного
сопротивления в режиме обратного КЗ
Решая уравнения (5), (8) и (9) с учётом уравнения связи:
A11 A22 − A12 A21 = 1,
получаем формулы для определения коэффициентов:
|
A11 = |
A12 = A11 Z2K, |
|
A21 = |
A22 = |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.