

Рис. 2.3. Рис. 2.4.
Решение.
1. Цепь рис. 2.3 содержит шесть ветвей (![]() ), четыре узла (
), четыре узла (![]() ), один источник тока
), один источник тока ![]() (
(![]() ).
).
Выберем положительные направления токов в схеме, как это указано на рис. 2.4.
2. Определим достаточное количество уравнений для расчета цепи по первому закону Кирхгофа:
![]() ,
,
по второму закону Кирхгофа:
![]() .
.
Достаточное количество уравнений равно пяти, что
соответствует числу неизвестных токов ![]() (рис.
2.4).
(рис.
2.4).
3. Составим систему уравнений по законам Кирхгофа.
Три уравнения по первому закону Кирхгофа, например, для узлов 2, 3 и 4. Два уравнения по второму закону Кирхгофа. Положительные направления обхода независимых контуров выберем в соответствии с указанными на рис. 2.4.
для узла 2: ![]() ;
;
для узла 3: ![]() ;
;
для узла 4: ![]() ;
;
для контура ![]() :
: ![]() ;
;
для контура ![]() :
: ![]() .
.
П р и м е ч а н и е: При выборе независимых контуров необходимо следить за тем, чтобы контур не содержал ветви с источником тока.
4. После подстановки числовых значений параметров элементов цепи получим:

5. Решение системы получим в матричной форме
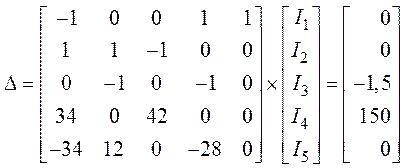 .
.
6. В результате решения матричной системы уравнений находим токи:
![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Знак минус у тока ![]() означает,
что действительное направление тока противоположно направлению, выбранному на
схеме рис.2.4.
означает,
что действительное направление тока противоположно направлению, выбранному на
схеме рис.2.4.
П р и м е ч а н и е: изменять знак тока на обратный не следует, так как это может привести к ошибке в дальнейших расчетах.
7. Правильность расчета установим путем проверки баланса мощностей. Мощность, поступающая в цепь от источников энергии должна равняться сумме мощностей потребителей электрической энергии:
![]() .
.
Предварительно найдем напряжение ![]() на зажимах с источником тока
на зажимах с источником тока ![]() (рис. 2.4). На основании второго
закона Кирхгофа получим:
(рис. 2.4). На основании второго
закона Кирхгофа получим:
![]() .
.
Полная мощность, развиваемая источниками энергии
![]()
![]() .
.
Полная мощность потерь в резистивных сопротивлениях
![]()
![]() .
.
Следовательно
![]() .
.
Погрешность расчета составляет:
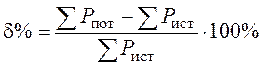
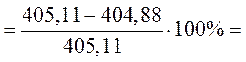
![]() .
.
Задача 2.3.
Для схемы электрической цепи (рис. 2.5) построить
график изменения потенциала во внешнем контуре. Параметры элементов цепи заданы
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.

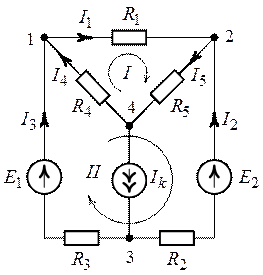
Рис. 2.5. Рис. 2.6.
Решение.
1. Предварительно выполним расчет токов внешнего
контура. Цепь (рис. 2.5) содержит шесть ветвей (![]() ),
четыре узла (
),
четыре узла (![]() ), один источник тока
), один источник тока ![]() (
(![]() ).
).
Выберем положительные направления токов в схеме цепи в соответствии с указанными на рис. 2.6.
2. Достаточное количество уравнений для расчета цепи
по первому закону Кирхгофа ![]() , по второму
закону Кирхгофа
, по второму
закону Кирхгофа ![]() .
.
Общее количество уравнений равно пяти.
3. Три уравнения по первому закону Кирхгофа составим для узлов 1, 2 и 4.
Два уравнения по второму закону Кирхгофа для контуров ![]() и
и ![]() обозначенных
в схеме на рис. 2.6.
обозначенных
в схеме на рис. 2.6.

4. Запишем систему в матричной форме
 .
.
5. После подстановки числовых значений получим
 .
.
6. Решение матричной системы позволяет определить токи
![]() ,
, ![]() ,
,
![]() .
.
7. Выделим элемент внешнего контура (рис. 2.7).
Примем потенциал точки 1 равным нулю (![]() ).
Рассчитаем потенциалы точек контура, обходя его по часовой стрелке:
).
Рассчитаем потенциалы точек контура, обходя его по часовой стрелке:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
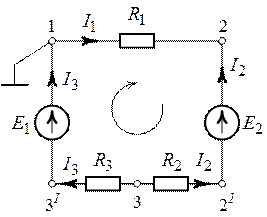
Рис. 2.7.
8. Порядок построения потенциальной диаграммы представлен на рис. 2.8. На диаграмме по оси абсцисс откладываем значения сопротивлений участков в последовательности расположения их в контуре.

Рис. 2.8.
Задача 2.4.
Определить показания вольтметров в схеме цепи рис. 2.9,
если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Внутреннее сопротивление
вольтметров принять равным
. Внутреннее сопротивление
вольтметров принять равным ![]() .
.
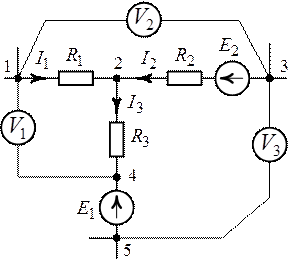
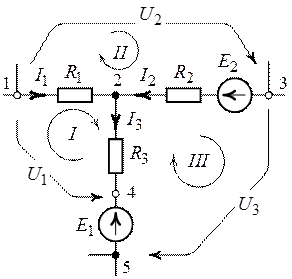
Рис. 2.9. Рис. 2.10.
Решение.
1. Заменим вольтметры, изображенные на схеме (рис. 2.9), векторами напряжений, указывающих на разность потенциалов между точками их подключения (рис. 2.10). Направления действия векторов напряжений выбираем произвольно.
2. Определим недостающий ток ![]() по
первому закону Кирхгофа
по
первому закону Кирхгофа
![]() .
.
3. Показание вольтметра ![]() определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура
определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура ![]() (рис. 2.10).
(рис. 2.10).
![]() ,
,
откуда
![]() .
.
4. Показание вольтметра ![]() определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура
определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура ![]() , рис. 2.10:
, рис. 2.10:
![]() ,
,
откуда
![]() .
.
5. Показание вольтметра ![]() определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура
определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура ![]() , рис. 2.10:
, рис. 2.10:
![]() ,
,
откуда
![]() .
.
Задача 2.5.
Определить показания приборов в схеме рис. 2.11, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Внутренние сопротивления
вольтметров принять
. Внутренние сопротивления
вольтметров принять ![]() , амперметров
, амперметров ![]() .
.
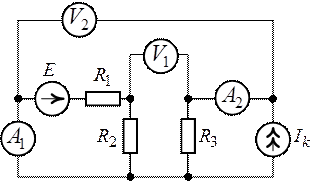

Рис. 2.11. Рис. 2.12.
Решение.
1. Выполним замену приборов с учетом их внутренних сопротивлений (рис. 2.12) и обозначим токи ветвей.
2. Показание амперметра ![]() равно
значению тока
равно
значению тока ![]() (рис. 2.12)
(рис. 2.12)
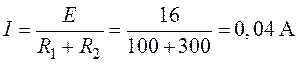 .
.
3. Показание амперметра ![]() будет
определяться током источника
будет
определяться током источника ![]() , включенным
последовательно в цепь с амперметром, т.е.
, включенным
последовательно в цепь с амперметром, т.е. ![]() .
.
4. Показание вольтметра ![]() определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура
определим
из выражения, записанного по второму закону Кирхгофа для замкнутого контура ![]() (рис. 2.12):
(рис. 2.12):
![]() ,
,
откуда
![]()
![]() .
.
5. Показание вольтметра ![]() определим
по выражению, записанному по второму закону Кирхгофа для замкнутого контура
определим
по выражению, записанному по второму закону Кирхгофа для замкнутого контура ![]() (рис. 2.12):
(рис. 2.12):
![]() ,
,
откуда
![]()
![]() .
.
Задачи для самостоятельного решения
Задача 2.6. В
цепи (рис. 2.13) ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Определить показания приборов, если
.
Определить показания приборов, если ![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]()
Задача 2.7. Определить
показание вольтметра в цепи рис. 2.14. Параметры цепи заданы: ![]() ,
, ![]() ,
, ![]() .
.
О т в е т: ![]() .
.
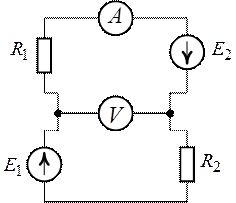
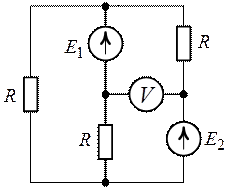
Рис. 2.13. Рис. 2.14.
Задача 2.8. Для
схемы на рис. 2.15, пользуясь законами Кирхгофа, найти все токи, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Задача 2.9.
Для схемы рис. 2.16, пользуясь законами Кирхгофа определить токи в ветвях с резистивными
сопротивлениями, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
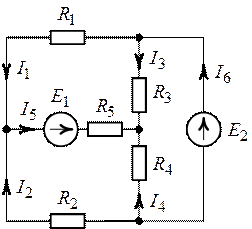
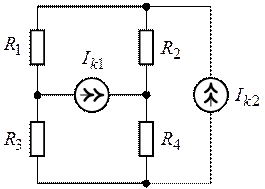
Рис. 2.15. Рис. 2.16.
Задача 2.10.
Для схемы рис. 2.17, пользуясь законами Кирхгофа определить все токи, если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() .
.
Задача 2.11. Напряжение
на входе цепи (рис. 2.18). составляет ![]() .
Определить напряжение
.
Определить напряжение ![]() на выходе цепи, если
на выходе цепи, если ![]()
![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() .
.
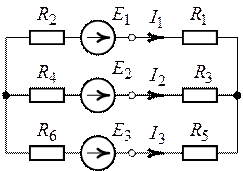
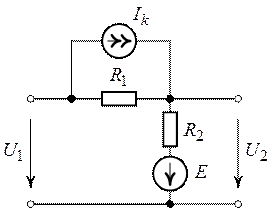
Рис. 2.17. Рис. 2.18.
Задача 2.12.
Определить токи в схеме рис. 2.19, если ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Проверить баланс мощностей.
. Проверить баланс мощностей.
О т
в е т: ![]() ,
, ![]() ,
, ![]() .
.
Задача 2.13.
Для схемы рис. 2.20, пользуясь законами Кирхгофа определить показания приборов,
если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Принять внутренние сопротивления приборов:
.
Принять внутренние сопротивления приборов: ![]() ,
, ![]() .
.
О т
в е т: ![]() ,
, ![]() .
.

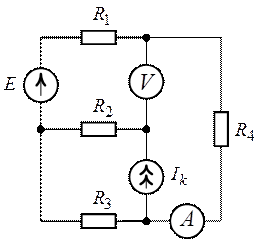
Рис. 2.19. Рис. 2.20.
Задача 2.14.
Для схемы рис. 2.21, пользуясь законами Кирхгофа определить все токи. Дано ![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т
в е т: ![]() ,
, ![]() .
.
Задача 2.15.
Рассчитать с использованием законов Кирхгофа токи в схеме рис.2.22, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Задача 2.16.
Для схемы рис. 2.23, пользуясь законами Кирхгофа определить все токи, если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
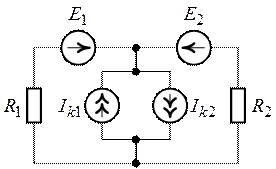
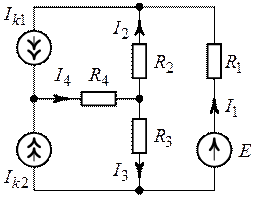
Рис. 2.21. Рис. 2.22.
Задача 2.17.
Для схемы рис. 2.24, пользуясь законами Кирхгофа определить все токи. Дано ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т
в е т: ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.

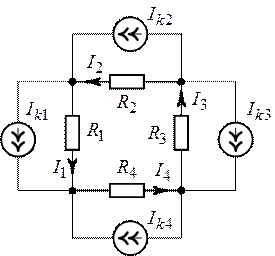
Рис. 2.23. Рис. 2.24.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.