Окончательно для токов ![]() ,
, ![]() получим (рис. 1.8)
получим (рис. 1.8)
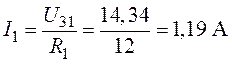 ;
;
 .
.
5. Ток ![]() определим из
уравнения, составленного по первому закону Кирхгофа для узла 1 (рис.1.6)
определим из
уравнения, составленного по первому закону Кирхгофа для узла 1 (рис.1.6)
![]() .
.
6. Из уравнений, составленных по первому закону
Кирхгофа, для узлов 3 и 2 (рис. 1.6) определим токи ![]() и
и
![]() :
:
![]() ;
;
![]() .
.
Задача 1.3.
Определить показание амперметра, установленного в
ветви с источником ЭДС (рис. 1.12), если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Внутренним сопротивлением амперметра можно пренебречь (
.
Внутренним сопротивлением амперметра можно пренебречь (![]() ).
).
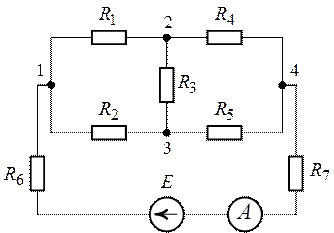
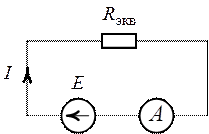
Рис. 1.12. Рис. 1.13.
Решение.
1. Методом свертывания цепи преобразуем схему рис. 1.12 к виду, приведенному на рис. 1.13.
Заменим треугольник сопротивлений, подключенный к точкам 1, 2 и 3 (рис. 1.12), эквивалентной звездой с вершинами 1, 2 и 3 (рис. 1.14).
Величины сопротивлений эквивалентной звезды:
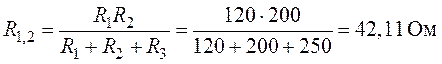 ;
;
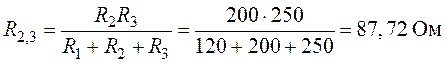 ;
;
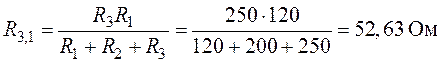 .
.
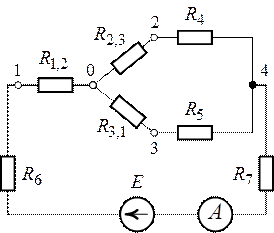

Рис. 1.14. Рис. 1.15.
Сопротивление ![]() соединено
последовательно с
соединено
последовательно с ![]() , а сопротивление
, а сопротивление ![]() последовательно с
последовательно с ![]() (рис. 1.14). Участок цепи с сопротивлениями
(рис. 1.14). Участок цепи с сопротивлениями
![]() и
и ![]() включен
параллельно участку с сопротивлениями
включен
параллельно участку с сопротивлениями ![]() и
и
![]() (рис. 1.14).
(рис. 1.14).
Общее сопротивление обоих участков схемы (рис. 1.15) равно:
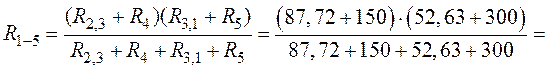
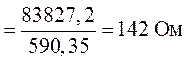 .
.
Сопротивления ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1.15) включены последовательно.
Эквивалентное сопротивление всей цепи (рис. 1.13)
(рис. 1.15) включены последовательно.
Эквивалентное сопротивление всей цепи (рис. 1.13)
![]()
![]() .
.
2. Показание амперметра соответствует току ![]() (рис. 1.13):
(рис. 1.13):
 .
.
Задача 1.4.
Определить величину источника тока, установленного на
входе цепи (рис. 1.16), если показание амперметра в разветвленной части схемы
составляет ![]() . Сопротивления резисторов
. Сопротивления резисторов ![]() равны
равны ![]() .
.
Внутреннее сопротивление источника ![]() . Внутренним сопротивлением
амперметра можно пренебречь (
. Внутренним сопротивлением
амперметра можно пренебречь (![]() ).
).
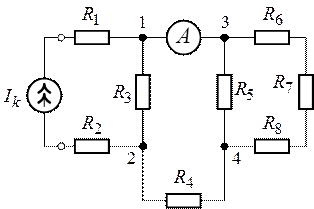

Рис. 1.16. Рис. 1.17.
Решение.
1. Пользуясь методом свертывания, приведем участок цепи (рис. 1.16) относительно узлов 3 и 4 к виду, представленному на рис. 1.17.
Общее сопротивление участка цепи
 .
.
2. Напряжение ![]() между
узлами 1 и 2 (рис. 1.17)
между
узлами 1 и 2 (рис. 1.17)
![]() .
.
3. Ток ![]() в ветви с
сопротивлением
в ветви с
сопротивлением ![]() (рис. 1.17)
(рис. 1.17)
 .
.
4. Ток источника ![]() на
входе цепи определим на основании первого закона Кирхгофа:
на
входе цепи определим на основании первого закона Кирхгофа:
![]() .
.
Задача 1.5.
В схеме (рис. 1.18) найти токи, применив метод
пропорционального пересчета, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
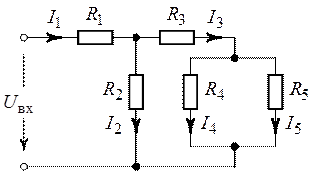
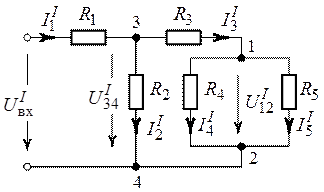
Рис. 1.18. Рис. 1.19.
Решение.
1. В рассматриваемой цепи зададим ток в одной из
удаленных от источника ветвей, например, с сопротивлением ![]() , равным
, равным ![]() и
определим некоторое напряжение источника на входе цепи
и
определим некоторое напряжение источника на входе цепи ![]() ,
при котором
,
при котором ![]() (рис. 1.19)
(рис. 1.19)
2. Определим токи ![]() (рис.
1.19)
(рис.
1.19)
Напряжение ![]()
![]() .
.
Ток ![]() равен:
равен: 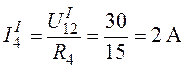 .
.
Ток ![]() определим как
сумму токов
определим как
сумму токов ![]() и
и ![]()
![]() .
.
Напряжение на сопротивлении ![]()
![]() .
.
Напряжение ![]() между узловыми
точками 3 и 4
между узловыми
точками 3 и 4
![]() .
.
Ток ![]() определим как
определим как
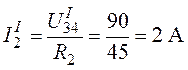 .
.
Ток ![]() на входе цепи
определим как сумму токов
на входе цепи
определим как сумму токов ![]() и
и ![]() :
:
![]() .
.
Напряжение на сопротивлении ![]()
![]() .
.
Напряжение на входе цепи
![]() .
.
3. Определим коэффициент пересчета как отношение
напряжения на входе цепи, заданного по условию задачи ![]() ,
к найденному при расчетах
,
к найденному при расчетах ![]() :
:
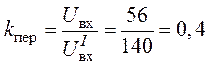 .
.
4. Действительные токи в ветвях цепи найдем как
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задачи для самостоятельного решения
Задача 1.6. Определить
эквивалентное сопротивление электрической цепи, представленной на рис. 1.20,
относительно зажимов 1 и 2, в которой сопротивления ![]() равны
равны
![]() .
.
О т в е т: ![]() .
.
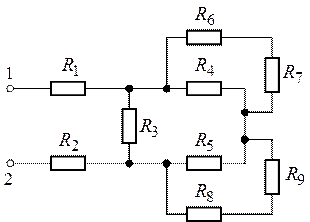
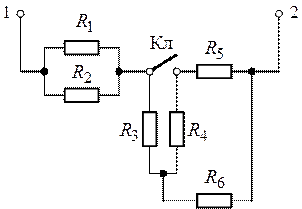
Рис. 1.20. Рис. 1.21.
Задача 1.7. Определить
эквивалентное сопротивление цепи (рис.1.21) между входными зажимами 1 и 2 при
разомкнутом и замкнутом положениях ключа (![]() ),
если
),
если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: при разомкнутом ключе ![]() ; при замкнутом ключе
; при замкнутом ключе ![]() .
.
Задача 1.8. Определить
токи в ветвях цепи (рис. 1.22), если задано ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Задача 1.9. В
схеме (рис. 1.23) определить токи во всех ветвях, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
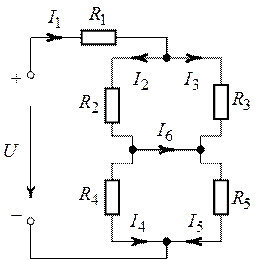
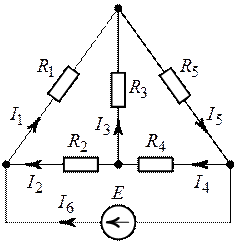
Рис. 1.22. Рис. 1.23.
Задача 1.10. Определить
токи во всех ветвях схемы (рис. 1.24), если задано ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Задача 1.11. В
электрической схеме рис. 1.25 определить токи во всех ветвях, если задано ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.

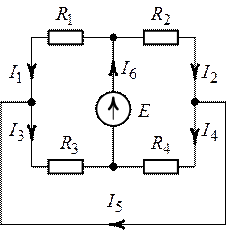
Рис. 1.24. Рис. 1.25.
Задача 1.12. Определить
показание амперметра для схемы рис. 1.26, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Принять
.
Принять ![]() .
.
О т в е т: ![]() .
.
Задача 1.13. Определить
показание амперметра для схемы рис. 1.27, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Принять
.
Принять ![]() .
.
О т в е т: ![]() .
.
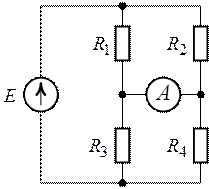
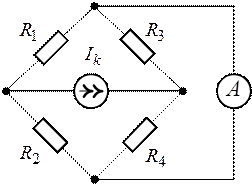
Рис. 1.26. Рис. 1.27.
Задача 1.10. Показание
амперметра (рис. 1.28), установленного в разветвленной части схемы, составляет ![]() . Найти величину источника тока
. Найти величину источника тока ![]() , если
, если ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Сопротивление источника считать
. Сопротивление источника считать ![]() , амперметра
, амперметра ![]() .
.
О т в е т: ![]() .
.
Задача 1.11. Найти
все токи в ветвях цепи, схема которой приведена на рис. 1.29, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Принять сопротивление источника
. Принять сопротивление источника ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.

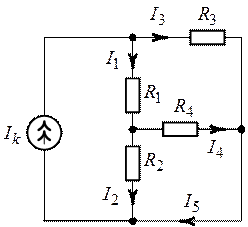
Рис. 1.28. Рис. 1.29.
Задача 1.12. Определить
показание амперметра в схеме (рис. 1.30), если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Принять
.
Принять ![]() .
.
О т в е т: ![]() .
.
Задача 1.13. Методом
пропорционального пересчета найти все токи в схеме рис. 1.31, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
В расчетах принять ток в сопротивлении
.
В расчетах принять ток в сопротивлении ![]() равным
равным
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
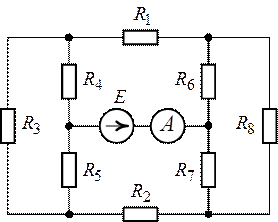
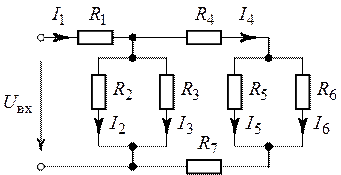
Рис. 1.30. Рис. 1.31.
2. РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ С ПОМОЩЬЮ ПРЯМОГО ПРИМЕНЕНИЯ ЗАКОНОВ КИРХГОФА
Законы Кирхгофа лежат в основе расчета сложных цепей содержащих несколько источников энергии. С помощью двух законов Кирхгофа устанавливаются соотношения между токами и ЭДС в ветвях электрической цепи и напряжениями на элементах цепи.
Задача 2.1.
Пользуясь законами Кирхгофа, рассчитать токи в
ветвях схемы рис.2.1, если ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Решение.
1. Цепь рис. 2.1 содержит три ветви (![]() ), два узла (
), два узла (![]() ).
Цепь питает два источника ЭДС
).
Цепь питает два источника ЭДС ![]() и
и ![]() . Источники тока в цепи отсутствуют (
. Источники тока в цепи отсутствуют (![]() ).
).
Выберем произвольно положительные направления токов в ветвях схемы и обозначим их как указано на рис. 2.2.
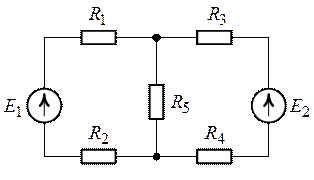

Рис. 2.1. Рис. 2.2.
2. Определим достаточное количество уравнений для расчета цепи по законам Кирхгофа.
По первому закону Кирхгофа:
![]() .
.
По второму закону Кирхгофа:
![]()
![]() .
.
Достаточное количество уравнений равно трем, что
соответствует количеству неизвестных токов, обозначенных в ветвях схемы как ![]() ,
, ![]() и
и
![]() (рис. 2.2).
(рис. 2.2).
3. Составим систему уравнений по первому и второму закону Кирхгофа. Одно уравнение по первому закону Кирхгофа, например, для узла 1 и два уравнения по второму закону Кирхгофа для двух независимых контуров. Положительные направления обхода контуров соответствуют направлениям, указанным на рис. 2.2.
для узла 1: ![]() ;
;
для контура ![]() :
: ![]() ;
;
для контура ![]() :
: ![]() .
.
4. После подстановки числовых значений имеем:

5. Решение системы получим с помощью определителей:
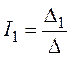 ;
; 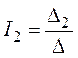 ;
;
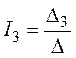 ,
,
где![]() – главный
определитель системы,
– главный
определитель системы, ![]() ,
, ![]() ,
,
![]() – алгебраические дополнения.
– алгебраические дополнения.
Главный определитель системы равен:
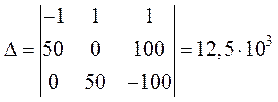 .
.
Дополнительные определители равны:
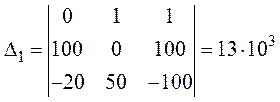 ;
;
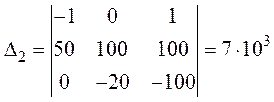 ;
;
 .
.
6. Токи в ветвях:
 ;
; 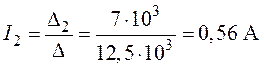 ;
;
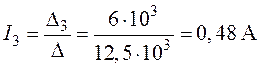 .
.
Задача 2.2.
Рассчитать с использованием законов Кирхгофа токи в
ветвях схемы изображенной на рис. 2.3, если известны ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Выполнить правильность расчета цепи
путем проверки баланса мощностей.
. Выполнить правильность расчета цепи
путем проверки баланса мощностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.