ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Электротехнический факультет
Кафедра электрических машин и аппаратов
Задачи: 2.1; 2.2; 2.3.
Дисциплина «Испытания и надежность ЭМ»
Вариант №8
Проверил: к.т.н., доцент Шестаков А.В.
Определить по результатам ресурсных испытаний следующие количественные характеристики надежности:
- вероятность безотказной работы (ВБР) ![]() за время
за время ![]() ;
;
- вероятность отказа ![]() за
время
за
время ![]() ;
;
- вероятность безотказной работы ![]() за
время
за
время ![]() ;
;
- вероятность отказа ![]() за
время
за
время ![]() ;
;
- интенсивность отказов 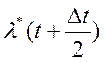 за
время
за
время 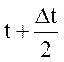 ;
;
- частоту отказов 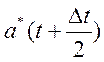 за
время
за
время 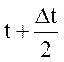 .
.
Исходные данные :
N0 = 200 – количество машин, поставленных на испытания;
t = 2000 часов – длительность основных испытаний;
Δt = 150 часов – длительность дополнительных испытаний;
n(t) = 35 – количество машин, отказавших за время t;
n(Δt) = 15 – количество машин, отказавших за время Δt.
Решение:
1. Вероятность
безотказной работы за время t, ![]() (t),
(t),
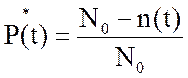 ,
,
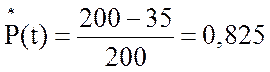 .
.
2. Вероятность
отказа за время t, ![]() (t),
(t),
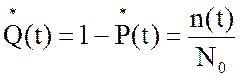 ,
,
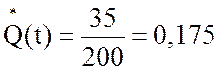 .
.
3. Вероятность
безотказной работы за время t+Δt,
![]() (t+Δt),
(t+Δt),
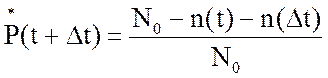 ,
,
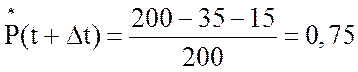 .
.
4. Вероятность
отказа за время t+Δt, ![]() (t+Δt),
(t+Δt),
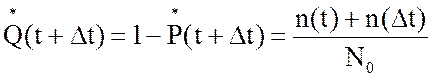 ,
,
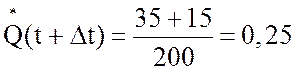 .
.
5. Среднее количество машин, исправно работающих на интервале [t;t+Δt], Nср,
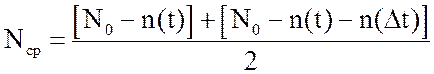 ,
,
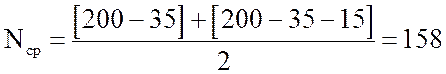 .
.
6.
Интенсивность отказов ![]() (t+Δt/2), ед/час,
(t+Δt/2), ед/час,
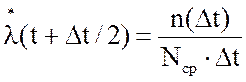 ,
,
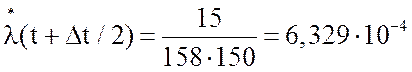 .
.
7. Частота
отказов ![]() (t+Δt/2), ед/час,
(t+Δt/2), ед/час,
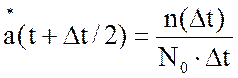 ,
,
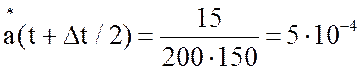 .
.
Задача 2.2
Оценить надежность ДПТ, работающего с номинальной нагрузкой, при различных законах распределения отказов его элементов:
- рассчитать вероятность безотказной работы (ВБР) отдельных узлов и ДПТ в целом за время 500, 1000, 2000, 5000 часов;
- построить график
ВБР ![]() .
.
Исходные данные :
![]() часов – среднее время безотказной
работы;
часов – среднее время безотказной
работы;
![]() – среднеквадратичное отклонение;
– среднеквадратичное отклонение;
![]() час
час![]() –
параметр масштаба;
–
параметр масштаба;
![]() – параметр асимметрии;
– параметр асимметрии;
![]() часов – среднее время безотказной
работы;
часов – среднее время безотказной
работы;
![]() часов – среднеквадратичное
отклонение;
часов – среднеквадратичное
отклонение;
Решение:
ДПТ разбивается на следующую схему:

Для ВБР обмотки принято, что она подчиняется логарифмически нормальному закону и определяется следующим образом:
![]()
где ![]() -
значение центрированной и нормированной функции;
-
значение центрированной и нормированной функции; ![]() -
аргумент этой функции; для логарифмически нормального закона это аргумент
равен:
-
аргумент этой функции; для логарифмически нормального закона это аргумент
равен:
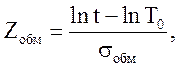
где ![]() -
текущее значение времени, час;
-
текущее значение времени, час; ![]() - натуральный
логарифм среднеквадратичного отклонения среднего времени безотказной работы
обмоток;
- натуральный
логарифм среднеквадратичного отклонения среднего времени безотказной работы
обмоток;
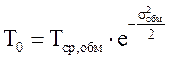
где ![]() -
среднее время безотказной работы обмоток, час.
-
среднее время безотказной работы обмоток, час.
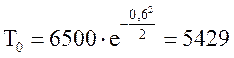
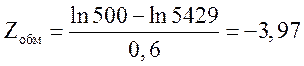
![]()
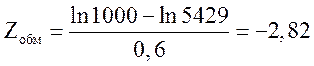
![]()
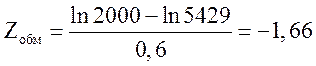
![]()
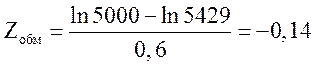
![]()
![]()
![]()
![]()
![]()
ВБР щеточно-коллекторного узла подчинена закону нормального распределения (закону Гаусса) и рассчитывается по формуле:
![]()
где ![]() -
значение центрированной и нормированной функции для аргумента:
-
значение центрированной и нормированной функции для аргумента:
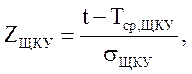
![]() - среднее время
безотказной работы щеточно-коллекторного узла, час,
- среднее время
безотказной работы щеточно-коллекторного узла, час, ![]() -
среднеквадратичное отклонение этого времени, час.
-
среднеквадратичное отклонение этого времени, час.
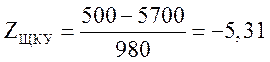
![]()
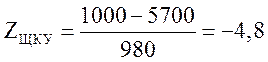
![]()
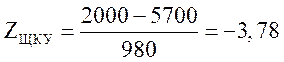
![]()
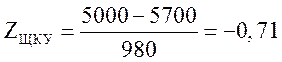
![]()
![]()
![]()
![]()
![]()
ВБР подшипников определяется распределением Вейбулла, который представляет собой следующую зависимость:
![]()
где ![]() - параметр, определяющий
масштаб,
- параметр, определяющий
масштаб, ![]() - параметр
асимметрии.
- параметр
асимметрии.
![]()
![]()
![]()
![]()
Результирующая ВБР двигателя постоянного тока за время t при последовательном соединении элементов в структуре его надежности равна:
![]() ,
,
![]()
![]()
![]()
![]()
Результаты расчетов заносим в таблицу 1.
Таблица 1 – Вероятность безотказной работы за время t
|
t, час |
500 |
1000 |
2000 |
5000 |
|
РДПТ |
0,9957 |
0,9849 |
0,926 |
0,4017 |
По данным таблицы 1 построена зависимость РДПТ(t).
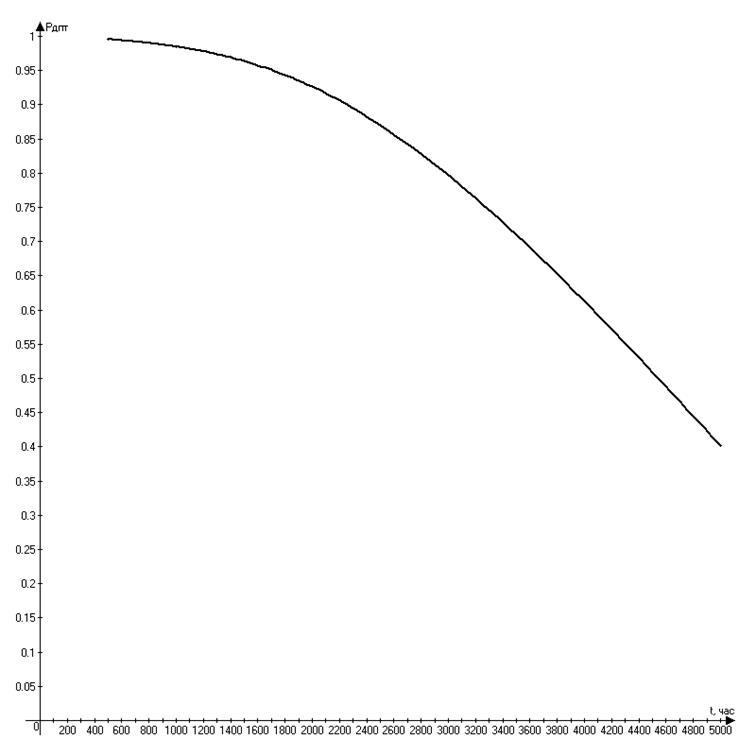
Рисунок 1 – Зависимость РДПТ = f(t).
Задача 2.3
Определить объем выборки n для проведения контрольных
испытаний на надежность по методу однократной выборки для подтверждения
заданной вероятности безотказной работы ![]() за
время t при риске заказчика β.
за
время t при риске заказчика β.
Определить время испытаний ![]() , необходимого
для подтверждения заданной вероятности безотказной работы
, необходимого
для подтверждения заданной вероятности безотказной работы ![]() за время t
при риске заказчика β в случае, когда на предприятии имеется
за время t
при риске заказчика β в случае, когда на предприятии имеется ![]() изделий, предназначенных для
испытаний. Среднеквадратичное отклонение принять равным
изделий, предназначенных для
испытаний. Среднеквадратичное отклонение принять равным ![]() .
.
Определить объемы выборки ![]() и
и
![]() для проведения контрольных испытаний
на надежность по методу двух выборок для подтверждения заданной вероятности
безотказной работы
для проведения контрольных испытаний
на надежность по методу двух выборок для подтверждения заданной вероятности
безотказной работы ![]() за время t
и риске заказчика β.
за время t
и риске заказчика β.
Исходные данные:
β=0,1 – риск заказчика;
![]() –
вероятность безотказной работы при риске β;
–
вероятность безотказной работы при риске β;
t=9000 часов – время работы;
![]() –
количество изделий, имеющихся для испытаний.
–
количество изделий, имеющихся для испытаний.
Решение:
Объем выборки:
n=22.
Определяем вероятность:
![]() .
.
Вычисляем значения центрированной и нормированной функции:
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
Определяем аргументы функций:
Z=1,3;
![]() .
.
Время испытаний, час:
![]() ;
;
где ![]() - среднеквадратичное
отклонение времени, час.
- среднеквадратичное
отклонение времени, час.
![]() ;
;
![]() .
.
Среднее время безотказной работы:
![]() ;
;
![]() .
.
Минимальное время испытаний:
![]() ;
;
![]() .
.
Максимальное время испытаний:
![]() ;
;
![]() .
.
Вычисляем значения центрированной и нормированной функции:
![]() ;
;
![]() .
.
Z=1,3.
Значение аргумента Z для нижней границы:
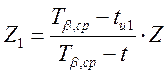 ;
;
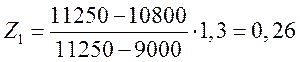 .
.
Значение аргумента Z для верхней границы:
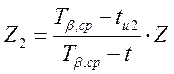 ;
;
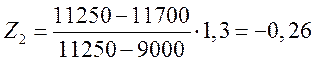 .
.
По значениям аргументов ![]() и
и ![]() определяются
соответствующие им значения центрированной и нормированной функции
определяются
соответствующие им значения центрированной и нормированной функции ![]() и
и ![]() :
:
![]()
![]() .
.
Вероятность безотказной работы за
минимальное время испытаний ![]() :
:
![]() ;
;
![]() .
.
Вероятность безотказной работы за
максимальное время испытаний ![]() :
:
![]() ;
;
![]() .
.
Определяем объем выборки ![]() и
и ![]() :
:
![]() ;
;
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.