Для построения картины поля в пазу необходимо измерить разности потенциалов между каждым узлом сетки в данном опыте и узлом 0. Предел вольтметра устанавливается таким образом, чтобы разность потенциалов между точками 0 и 1' была максимальной. Необходимо измерять потенциалы узлов не только крупных, но и мелких ячеек. Результаты измерения записываются на чертеже возле каждого узла.
В отчете приводится картина поля. Для ее построения следует соединить линиями точки с приблизительно равными потенциалами.
4.4 К пункту 3.4
Коэффициент воздушного зазора (коэффициент Картера) kδ можно определить на модели «невозбужденного» паза для любого отношения b1/δ и t1/δ при заданном bш/δ, гдеt1 – зубцовое деление, b1 – ширина зубца статора. Для его нахождения необходимо знать два напряжения:
– Ut1max – соответствующее максимальной индукции в зазоре Bm;
– Ut1 – соответствующее амплитуде первой гармоники индукции в воздушном зазоре B1m, которая меньше Bm вследствие зубчатости статора.
Если бы статор не имел зубцов, то поток был бы пропорционален максимальной индукции, умноженной на половину зубцового деления:
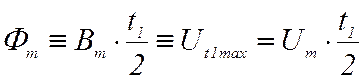, (15)
где Um – по формуле (13), а t1 – число крупных ячеек сетки, укладывающихся на одном зубцовом делении.
Напряжение Ut1 в данной модели определяется как U0 -55 – напряжение между осью паза и точкой, где индукция остается неизменной (между узлами 0 и 55).
Таким образом, коэффициент воздушного зазора в сеточной модели определяется следующим образом:
.
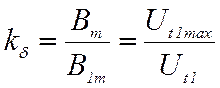(16)
Для сравнения следует определить коэффициент Картера по формуле, широко используемой при проектировании электрических машин:
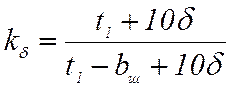. (17)
При расчете коэффициента воздушного зазора по формулам (15), (16) и (17) следует помнить, что значения зубцового деления t1, ширины шлица bш и воздушного зазора δ выражаются соответствующим количеством крупных ячеек модели. При этом следует иметь в виду, что на модели приведена только половина паза, следовательно, например, для глубокого открытого паза t1=2×(6+8)=28 крупных ячеек, bш=2×6=12 крупных ячеек.
4.5 К пункту 3.5
Для того, чтобы собрать схему глубокого паза с током следует отключить питание от вертикальной оси (размыканием ключа К3), разъединить перемычку и узлы 1' – 10' и 35' – 39', соединить проводниками узлы с 16' по 22' и замыканием ключа К2 подать напряжение на дно паза.
Снятие кривой распределения индукции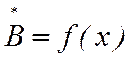 
проводится аналогично пункту 4.2. Напряжение
Um из
формул (13) и (14) следует рассчитывать для данной схемы. Результаты измерения заносятся в таблицу 1.
Построение картины поля глубокого паза с током ведется аналогично пункту 4.3. Полученная картина поля также приводится в отчете.
4.6 К пунктам 3.6, 3.7 и 3.8
Схема для исследования поля в мелком «невозбужденном» пазу собирается следующим образом: размыкается ключ К2, разъединяются узлы 28' – 34', соединяются проводниками с перемычкой узлы 35' – 39', замыканием ключа К4 подается напряжение на вертикальную ось мелкого паза.
Для схемы «невозбужденного» глубокого паза с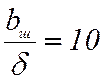 
необходимо:
– отключить тумблеры К1 – К4;
– соединить верхнюю и нижнюю части основной сетки паза замыканием узлов с 28' по 34';
– соединить верхнюю и нижнюю части дополнительной сетки замыканием узлов 10' – 14' дополнительных зон 1 и 2, расположенных справа и слева от основной сетки;
– соединить основную и дополнительную сетки паза с помощью замыкания узлов 1' – 10' основной сетки и дополнительной зоны 1, расположенной слева, а также узлов 35' – 39' основной сетки и дополнительной зоны 2, расположенной справа;
– соединить с узлами перемычки 15' соседние с ней узлы дополнительных зон 1 и 2;
– подать на вертикальную ось полученной модели напряжение с помощью ключа К1.
Схема «невозбужденного» полузакрытого паза с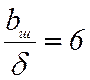 
собирается в следующем порядке:
– отключить тумблеры К1 – К4 и разъединить все узлы модели;
– соединить верхнюю и нижнюю части основной сетки паза замыканием узлов с 28' по 34';
– соединить узлы 1' – 10' дополнительной зоны 1 с узлами основной сетки, расположенными рядом;
– соединить узлы с 1' по 10' и с 35' по 39' на основной сетке с расположенными рядом узлами перемычки;
– подать на вертикальную ось модели напряжение с помощью ключа К3.
Исследование распределения индукции 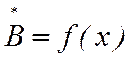вдоль пазового деления проводится
аналогично пункту 4.2. Напряжение Um из формул
(13) и (14) следует рассчитывать для каждой схемы в отдельности. Результаты измерения заносятся в таблицу 1. Кривые
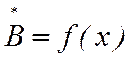распределения индукции в воздушном зазоре для
всех схем, исследуемых в лабораторной работе, строятся на одном графике
по рекомендациям пункта 4.2.
Определение коэффициента воздушного зазора kδ производится аналогично пункту 4.4. При этом необходимо учитывать в формулах (15), (16) и (17) напряжения Um и U0 -55 , а также размеры паза для каждой схемы отдельно.
5 Контрольные вопросы
5.1 Что описывают уравнения Пуассона и Лапласа?
5.2 Уравнение Лапласа в разностной форме.
5.3 Доказать аналогию между уравнением потенциалов сеточной модели и уравнением Лапласа.
5.4 Как записываются и что выражают граничные условия на сеточной модели?
5.5 Связь между потенциалами узлов сеточной модели, векторным магнитным потенциалом, магнитным потоком и индукцией.
5.6 Аналогия между магнитным полем и полем электрического тока. Как выглядит картина поля в пазу с током и при униполярном намагничивании?
5.7 Что влияет на характер распределения индукции в воздушном зазоре?
5.8 Что выражает коэффициент воздушного зазораkδ?
6 Библиографический список
6.1 Копылов И.П. Математическое моделирование электрических машин. – М.: 2001.
6.2 Сипайлов Г.А., Кононенко Е.В. Хорьков К.А. Электрические машины (специальный курс) – М.: Высшая школа, 1987.
6.3 Якимов В.В. Электрические машины. Спецкурс для студентов технологической специализации. – Горький, изд-во ГГУ,1988.
6.4 Петров Г.Н. Электрические машины. – М.: Энергия, 1985
|
|
Рисунок 4 – Схема стенда «Сеточная модель»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.