Моделирование на сеточной модели магнитного поля воздушного зазора при односторонней зубчатости статора: Методические указания к лабораторной работе № 2, страница 2

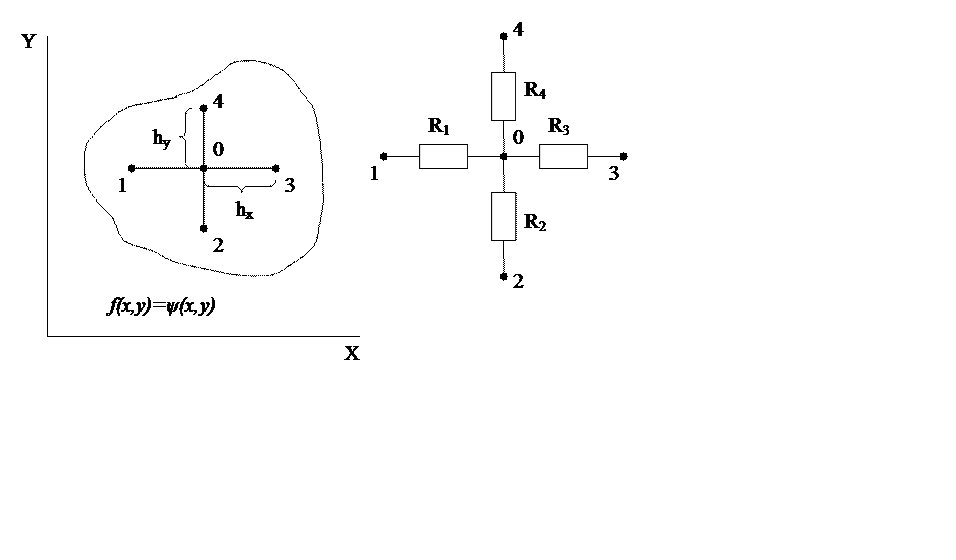
Рисунок 1 – К решению уравнения Лапласа на сеточной модели

Обратимся теперь к элементу электрической цепи, образованному из четырех сопротивлений, соединенных общей точкой (рисунок 1).

Первый закон Кирхгофа (сумма токов, сходящихся в узле, равна нулю) записывается для такой цепи в виде:

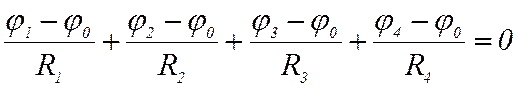,                          (5)

где φ_i – электрический потенциал i-й точки. При равенстве сопротивлений R₁=R₃ и R₂=R₄ выражение (5) преобразуется к виду:

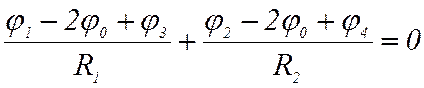.                              (6)

Если в соотношении (4) вместо h_x и h_y записать соответственно R₁ и R₂, вместо значений функции ψ(x,y) в точках 0…4 подставить электрические потенциалы этих точек и приравнять нулю , то получим полную аналогию уравнений (4) и (6).

Все сказанное свидетельствует о возможности замены элементарной площадки непрерывной среды размером 2h_x × 2h_y на ячейку из четырех ортогонально соединенных сопротивлений. При этом дифференциальные зависимости (4) заменяются разностными соотношениями (6), причем расхождения между ними определяются степенью разбиения пространства (h_x, h_y) и порядком высших производных искомой функции ψ(x,y).

Рисунок 2 – Ячейки сеточной модели

Представим произвольную область существования функции ψ(x,y) в виде совокупности элементарных площадей и заменим каждую из площадей ячейкой, изображенной на рисунке 2, как бы покрыв все пространство сеткой из сопротивлений R₁=R_x и R₂=R_y, соединенных в узлах. Получим, таким образом, сеточную модель, для которой справедливо уравнение Лапласа (1).

При равенстве всех сопротивлений сетки R₁ = R_x = R₂= R_y уравнение ее узловых потенциалов будет иметь вид:

.                                     (7)

Задав для воспроизведенной области условия, аналогичные граничным условиям в изучаемой области, можно получить значения исходной функции ψ(x,y) путем измерения потенциалов в узлах модели.

Прямоугольная сетка – не единственный возможный вариант моделирования сплошной среды. Известны треугольная, шестиугольная и другие сетки, для узловых потенциалов которых уравнение узловых потенциалов будет иметь свой вид. С помощью сетки можно моделировать не только в прямоугольных, но и в полярных координатах, а также создавать модели многомерных пространств. Задавая на сетках источники токов и напряжений, можно решать на них различные уравнения, в том числе и нестационарных процессов.

В качестве дискретных элементов сеточной модели обычно используются резисторы, которые могут быть изготовлены весьма точно. Параметры их стабильны и не зависят от воздействия внешних факторов.

2.2 Граничные условия на сеточной модели

На сеточных моделях, как и на моделях, изготовленных из сплошных сред, возможны два способа моделирования.

Электрический потенциал узла может соответствовать либо потенциальной функции, либо функции потока. Оба способа абсолютно идентичны, так как названные функции ортогональны и отличаются лишь системой задания условий на границах сетки. При исследовании плоскопараллельного магнитного поля в зоне воздушного зазора с односторонней зубчатостью удобно линиям равного электрического потенциала φ поставить в соответствие линии постоянного векторного магнитного потенциала A_z=const. Таким образом, имеется обратная аналогия между силовыми линиями магнитного и электрического поля (линиям равного электрического потенциала соответствуют силовые линии магнитного поля, а линии равного магнитного потенциала соответствуют линиям электрического тока). Тогда выражения для составляющих векторов индукции в прямоугольных координатах запишутся в виде:

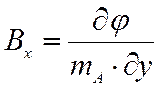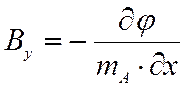;   ,                                    (8)

где  m_A –масштаб подобия между A_z и φ.

В данной работе моделируется магнитное поле в воздушном зазоре электрической машины с односторонней зубчатостью.

Решение уравнений (8) для поля  в исследуемой зоне при бесконечной глубине паза получено аналитически с помощью метода конформных преобразований. Из кривой индукции B (кривая 1 на рисунке 3) видно, что при удалении от зоны паза индукция на поверхности ротора очень быстро возрастает до максимального значения, определяемого разностью магнитных потенциалов статора и ротора и воздушным зазором δ.  Известно, что при достаточно большом удалении от зоны паза индукция в воздушном зазоре имеет только одну составляющую – по оси y  – по всей высоте воздушного зазора δ, то есть

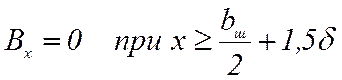,                                 (9)

где b_ш – ширина шлица паза.

Отсюда следует, что 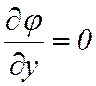, а значит, в пределах указанной области  φ(y)=const.

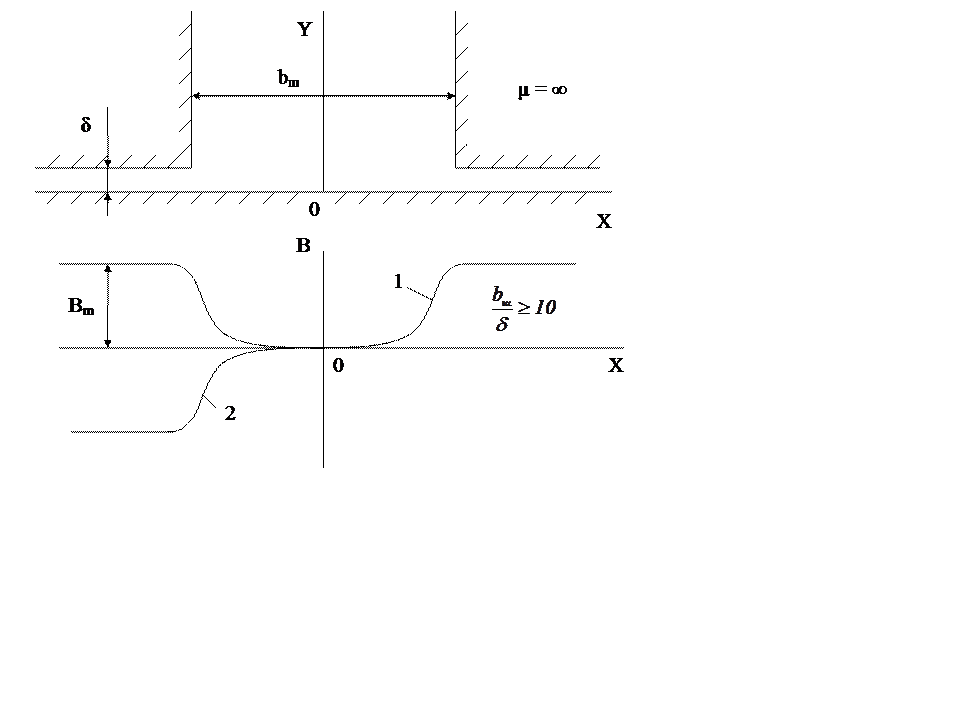
Рисунок 3 – Распределение индукции в воздушном зазоре вдоль пазового деления

электрической машины.

Очевидно, что если в пазу в пределах 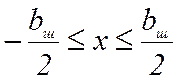 нет обмоток с токами, то составляющая индукции по оси x равна нулю также и при x = 0, а картина распределения индукции вдоль пазового деления симметрична относительно оси y. Из этого следует:

– при изучении поля в данной области можно ограничиться зоной x≥ 0;

– при x = 0 φ(y)=const.

В соответствии с последним условием замкнем накоротко модель по двум прямым: по оси y (x = 0) и на значительном удалении от паза, где индукция направлена только по оси y (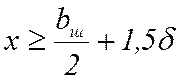). Присоединим к полученным эквипотенциалям источник ЭДС. Каждый узел сетки примет соответствующий потенциал φ, пропорциональный значению функции векторного магнитного потенциала A_z в этой точке.

Разность потенциалов между любыми двумя точками i и i+1 будет соответствовать магнитному потоку Φ_i, проходящему между этими двумя точками, отнесенному к единице длины по оси машины:

 .                               (10)

Так как 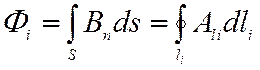, то в случае плоскопараллельного поля:

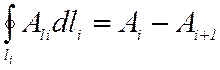.                                              (11)

Индукция же в любой точке К определяется как отношение разности узловых потенциалов сетки  к длине соответствующего отрезка между точками i и i+1, между которыми лежит точка К, причем расстояние между i-й и  (i+1)-й точками не должно быть слишком велико для того, чтобы можно было считать в окрестности точки К индукцию неизменной

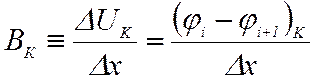.                                       (12)

 В случае, когда в пазу находятся обмотки с током, поле будет симметричным с переменой знака относительно оси паза (кривая 2 на рисунке 3), что также позволяет ограничиться рассмотрением лишь половины пазового деления. На оси паза имеет место только составляющая индукции по оси x. Считая весь ток сосредоточенным на дне паза, можно в модели задать равный электрический потенциал на дне паза.