Определение ускорения силы тяжести с помощью универсального маятника, страница 3

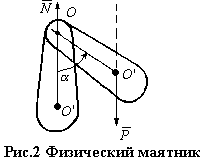
Тело, совершающее колебания около неподвижной оси, не проходящей через его центр масс, называется физическим маятником. В данном случае тело совершает возвратно-вращательное движение. На рис.2 О след оси вращения на плоскости чертежа; ОО¢= –  расстояние от оси вращения до центра тяжести. К телу приложены силы: сила тяжести  и реакция оси . Момент относительно оси вращения создает только сила . Уравнение движения маятника запишется в виде:

                                                                ,                                                       (6)

где  – момент инерции тела относительно оси колебания;

       – угловое ускорение тела;

      .

В выражении для М знак «–» имеет то же объяснение, что и в случае математического маятника. После соответствующих подстановок приходим к уравнению движения в виде:

                                                         .                                           (7)

Для случая малых колебаний уравнение запишется в виде

                                                          ,                                                  (8)

где .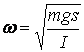

Решением данного дифференциального уравнения будет функция

                                                         .                                           (9)

Амплитуда колебаний  и начальная фаза определяются начальными условиями, а вот частота и период колебаний Т определяются параметрами физического маятника

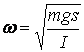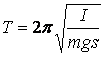                                                      ;  .                              (10)

Здесь мы снова видим, что колебания маятника изохронны, таким образом в принципе эти формулы можно использовать для определения ускорения силы тяжести.

2.  ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Универсальный маятник представляет собой прибор, соединяющий маятник, являющийся имитацией математического, и оборотный физический маятник.

Строго говоря, в установке скомбинированы 2 физических маятника, однако при условии, что длина нити, на которой подвешен шарик, много больше его размеров  позволяют этот маятник принять за математический.

В случае  проведения эксперимента с математическим маятником возникает проблема с определением . Строго говоря,  представляет собой расстояние от точки подвеса до центра тяжести шарика, но это расстояние точно зафиксировать нельзя.

Для исключения возникающей значительной погрешности можно поступить так. Измерим период колебаний Т₁ при длине нити , измеренной от центра колебаний до точки крепления нити на шарике. Таким образом, мы задаем некоторое неизвестное нам значение длины маятника . Затем измерим период колебаний Т₂ при длине нити  (длина маятника станет ).