


l395
Круговая диаграмма четырёхполюсника
При решении определённого класса задач, связанных с анализом цепей синусоидального тока, необходимо знать, как ведёт себя напряжение или ток на участке цепи при изменении модуля какого-либо из сопротивлений, если остальные параметры цепи остаются постоянными. Наряду с аналитическим решением, такая задача имеет графическое решение. Сущность этого решения заключается в построении геометрических мест концов вектора напряжения или тока. Полученные кривые называют диаграммами. Если эти кривые есть дуги окружностей, то диаграмма называют круговыми [1].
 |
Рис. 1
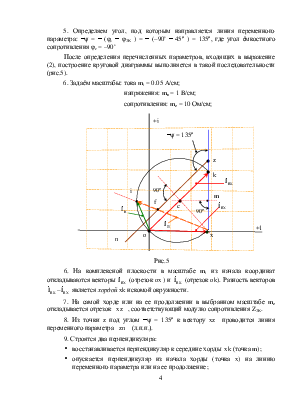
Представим разветвлённую цепь,
содержащую источники, активным четырёхполюсником. К входным зажимам подключена
ветвь с определяемым током ![]() , а
к выходным зажимам подключена ветвь с изменяемым сопротивления Z2. Получим
соотношение описывающие поведение вектора тока
, а
к выходным зажимам подключена ветвь с изменяемым сопротивления Z2. Получим
соотношение описывающие поведение вектора тока ![]() при изменении модуля сопротивления |Z2|.
при изменении модуля сопротивления |Z2|.
Используем свойство линейных цепей: между двумя токами цепи существует линейное соотношение вида
![]() = A + B
= A + B ![]() , (1)
, (1)
где A и B комплексные постоянные. Пусть Z2 = Z2 ejφ2. Z2 изменяется в приделах от 0 до ∞.
Рассмотрим два режима работы четырёхполюсника.
1. Режим холостого хода со стороны выходных зажимов:
![]() = 0, Z2 = ∞. и
= 0, Z2 = ∞. и
![]() = A. (2)
= A. (2)
2. Режим короткого замыкания со стороны выходных зажимов:, Z2 = 0,
![]() = A + B
= A + B
![]() =
= ![]() + B
+ B
![]()
Определим B
= (![]() –
– ![]() )/
)/![]() . (3)
. (3)
Подставим (3) и (2) в (1) получим:
![]() =
= ![]() +
+ 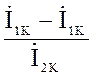
![]() , (4)
, (4)
Запишем ток ![]() методом эквивалентного генератора
методом эквивалентного генератора
![]() =
= 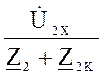 =
= 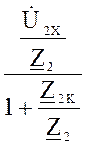 =
= 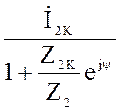 , (5)
, (5)
где Z2K
входное сопротивление цепи, рассчитываемое относительно
зажимов переменного сопротивления, и ψ = φ2 - φ2K разница углов переменного и входного
сопротивлений; ![]() - напряжение холостого хода на выходных зажимах при Z2 = ∞.
- напряжение холостого хода на выходных зажимах при Z2 = ∞.
Подставим (5) в (4) получим:
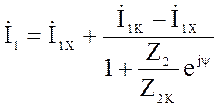 , (6)
, (6)
Комплексное выражение (6) геометрически
представляет дугу окружности [1], по которой скользит конец вектора тока ![]() , при изменении модуля сопротивления Z2.
, при изменении модуля сопротивления Z2.
Порядок построения круговой диаграммы
Порядок построения круговой диаграммы рассмотрим на примерах.
Пример 1.
Для цепи (рис.
2) требуется построить круговую диаграмму для тока ![]() при изменении модуля
сопротивления Xc.
По круговой диаграмме определить величину тока
при изменении модуля
сопротивления Xc.
По круговой диаграмме определить величину тока ![]() при Xc = 35 Ом.
при Xc = 35 Ом.
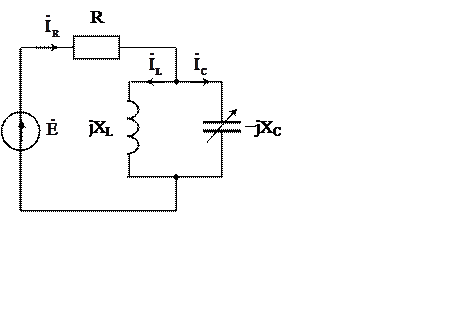 |
|||
|
|||
Рис.2
1. Выражение для тока ![]() представляется в виде дуги окружности в комплексной форме
записи:
представляется в виде дуги окружности в комплексной форме
записи:
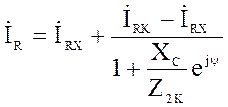 . (2)
. (2)
2. Определяем ![]() - ток холостого хода.
- ток холостого хода.
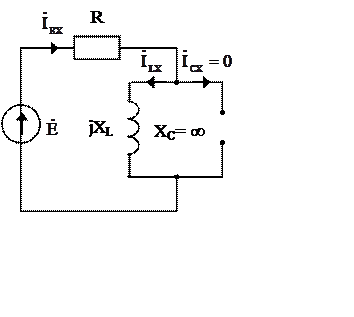 |
|||
|
|||
Рис.2
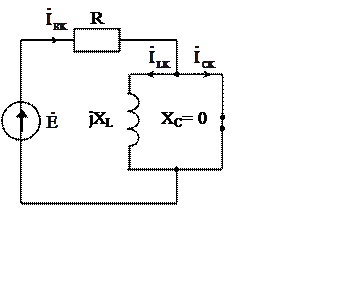 3.
Определяем
3.
Определяем ![]() -
ток короткого замыкания .
-
ток короткого замыкания .
|
Рис.3
4. Определяем Z2K входное сопротивление цепи относительно зажимов переменной ёмкости XC.
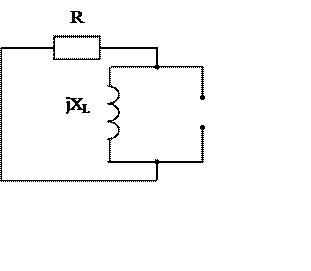 |
|||
|
|||
Рис.4
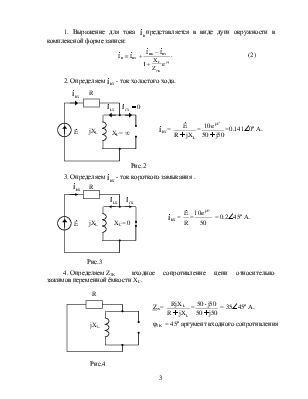
5. Определяем угол, под которым направляется линия переменного параметра: -ψ = - (φс - φ2K ) = - (–90o - 45º ) = 135º, где угол ёмкостного сопротивления φc = –90o
После определения перечисленных параметров, входящих в выражение (2), построение круговой диаграммы выполняется в такой последовательности (рис.5).
6. Задаём масштабы: тока mi = 0.05 A/см;
напряжения: mu = 1 B/см;
сопротивления: mz = 10 Ом/см;
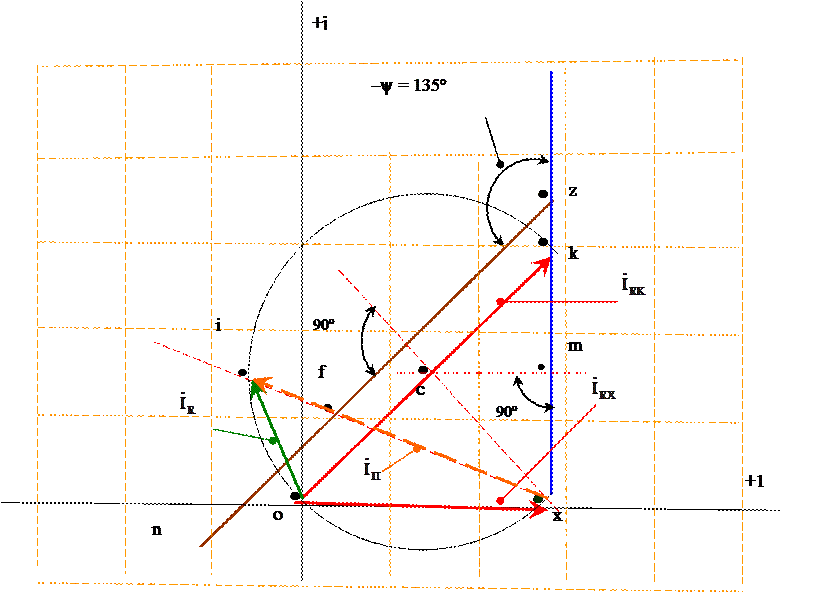 |
Рис.5
6. На комплексной плоскости в
масштабе mi из начала
координат откладываются векторы ![]() (отрезок
ox ) и
(отрезок
ox ) и ![]() (отрезок ok). Разность векторов
(отрезок ok). Разность векторов ![]() –
–![]() является хордой xk искомой окружности.
является хордой xk искомой окружности.
7. На самой хорде или на ее продолжении в выбранном масштабе mz откладывается отрезок xz , соответствующий модулю сопротивления Z2K.
8. Из точки z под углом -ψ = 135º к вектору xz проводится линия переменного параметра zn (л.п.п.).
9. Строятся два перпендикуляра:
восстанавливается перпендикуляр к середине хорды xk (точка m);
опускается перпендикуляр из начала хорды (точка x) на линию переменного параметра или на ее продолжение;
центр окружности лежит в точке пересечения этих двух перпендикуляров (точка c).
рабочая часть окружности располагается со стороны линии переменного параметра (л. п. п.).
10. В масштабе mz на линии переменного параметра отложить модуль переменного сопротивления XC (отрезок zf).
11. Из начала
хорды (точка x) через точку f провести
прямую до пересечения с дугой окружности (точка i). Точка пересечения этой
прямой с дугой окружности является концом вектора ![]() (точка i).
(точка i).
12. Из (2) видно, что ток ![]() определяется
суммой векторов:
определяется
суммой векторов:
![]() =
=
![]() +
+ ![]() ,
,
где ![]() =
=
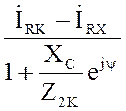 - переменный
вектор, определяется отрезком xi.
- переменный
вектор, определяется отрезком xi.
При изменении XC
каждый раз к неизменному вектору ![]() добавляется переменный вектор
добавляется переменный вектор ![]() , величина
и направление которого зависит от XC. Правильно построенная круговая
диаграмма позволяет получить целый ряд зависимостей в схеме: напряжений, токов,
мощностей от изменения модуля переменного сопротивления XC [1].
, величина
и направление которого зависит от XC. Правильно построенная круговая
диаграмма позволяет получить целый ряд зависимостей в схеме: напряжений, токов,
мощностей от изменения модуля переменного сопротивления XC [1].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.