







 1.
1.
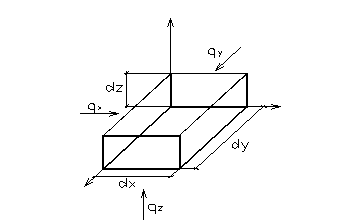
Ур-е температурного поля этого эл-та в диф-ой форме может быть получено из закона сохранения энергии и будет равно: dQт=dQв+dQu; dQт-изменение теплосодержания элемента; dQв- теплота полученная эл-том извне ч/з его границы путем теплопроводности; dQu- теплота источников внутри тела; Сумма количеств теплоты, прошедшее ч/з 6 граней эл-та определит теплоту получаемую телом извне: dQв= dQх+ dQy+ dQz- dQх+dx- dQy+dy-dQz+dz; dxdydz=dV;
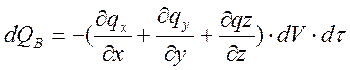 ; dQu=qudVdτ;
; dQu=qudVdτ; 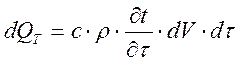 ;
;
qu-теплота выдел-я в объёме тела; с-теплоёмкость мат-ла; ρ-плотность мат-ла;
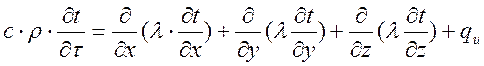 ; Это выражение есть общая форма
диф-го ур-я теплопровдности или ур-е температурного поля. Это ур-е
устанавливает зависимость темп-ры от координат и времени в диф. форме.
; Это выражение есть общая форма
диф-го ур-я теплопровдности или ур-е температурного поля. Это ур-е
устанавливает зависимость темп-ры от координат и времени в диф. форме.
Если теплопроводность мат-ла не зависит от координат и темп-ры, то ур-е примет вид:
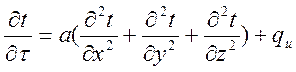
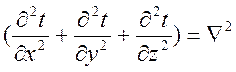 -
оператор Лапласа;
-
оператор Лапласа;
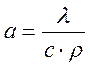 - коэф. температуропроводности;
- коэф. температуропроводности;
В случаях, когда темп-ра не зависит от 1 или 2х координат, соотв-но будут отсутствовать 1 или 2 слагаемых и темп-е поле будет называться одномерным или двухмерным.
2.
Условия однозначности включают в себя пространственные или временные условия:
Пространственные условия определяются:
а) формами и размерами обл-ти или тела для которого опр-ся темп.поле;
б) распределением или полем физ-их св-в. Физ-е св-ва могут быть одинаковыми для всей области или зависеть от темп-ры и тогда они будут переменными в разл. частях тела;
в) граничные условия ( условия на границе области) они могут быть заданы по-разному:
- на границе области задана темп-ра, она может быть пост-ой или изменяться во времени, такие условия называют граничные условия 1го рода; tг=f(x,y,z,τ);
- задана плотность теплового потока для всех точек грницы области - граничные условия 2го рода; q=f(x,y,z,τ);
- задана темп-ра среды, контактирующей с пов-тью тела и закон ткплообмена м/у ними. Чаще всего этот закон представлен в виде простейшего ур-я Ньютона - граничные условия 3го рода;
dQ=α(tср-tг)dF; tср- темп-ра среды задана; α- коэф.теплообмена задан;
-
граница области (тела) контакт-го с другим телом и этот контакт абсолютен, при
этом равенство темп-р тел и плотностей тепловых потоков на пов-ти контакта задаются
выр-ми- граничные условия 4го рода; tг1=tг2; qг1=qг2; 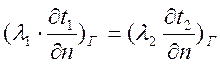
При решении практических задач задаются условия 3го и 4го рода.
г) временные или начальные условия. Определяет темп-е поле в некоторый момент времени; t=f(x,y,z) τ=0.
3.
Кол-во тепла проходящее ч/з пов-ть площадки в единицу времени называется тепловым потоком (Вт, Дж, Ккал/ч)
Поток отнесенный к площади называется удельным тепловым потокам q (Вт/м2, Дж/м2, Ккал/м2)
Закон
Фурье: кол-во тепла переданным теплопроводностью ч/з элементарную площадку
изотермической поверхности пропорционально grad t
взятого с обратным знаком, времени и величине этой площади. 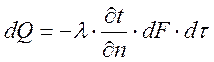 ; dQ- кол-во тепла
или тепловой поток.
; dQ- кол-во тепла
или тепловой поток.
λ-коэф.теплопроводности;
![]() - вектор, хар-щий изменение темп-ры
по направлению;
- вектор, хар-щий изменение темп-ры
по направлению;
![]() - размер эл-ой площадки;
- размер эл-ой площадки; ![]() - интервал времени;
- интервал времени; 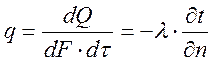 ;
;
q- удельный тепловой поток;
4.
Тепловое подобие определяет условие при котором системы подобные геометрически и механически подобны и тепловом отношении.
1.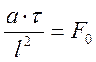 - число Фурье. Этот комплекс Фурье
как и число гомохромности устанавливает сходственные моменты времени.
- число Фурье. Этот комплекс Фурье
как и число гомохромности устанавливает сходственные моменты времени.
2.
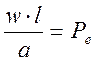 - число Пекле. Определяет влияние на
теплообмен дв-я жидкости.
- число Пекле. Определяет влияние на
теплообмен дв-я жидкости.
Число
Пекле можно преобразовать, представив в виде произведения комплексов: 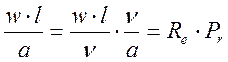 Такая замена удобна, т.к. число Re –
число гидромеханического подобия, а Pr составлен только из
теплофизических хар-к ж-ти и соотв. хар-ет её.
Такая замена удобна, т.к. число Re –
число гидромеханического подобия, а Pr составлен только из
теплофизических хар-к ж-ти и соотв. хар-ет её.
3.
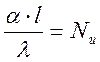 - число Нюсельта. Хар-ет условие
теплообмена м/у ж-тью и стенкой.
- число Нюсельта. Хар-ет условие
теплообмена м/у ж-тью и стенкой.
Таким образом при тепловом подобии 2х или неск-их систем критерии Фурье, Пекле, Нюсельта для сходственных точек должны иметь одинаковые значения.
5.
При λ=const. 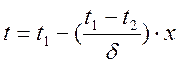 - распределение
темп-ры в стене;
- распределение
темп-ры в стене;
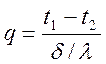 ( Вт/м2)
- тепловой поток →
( Вт/м2)
- тепловой поток → 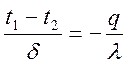 ;
; 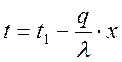 - темп-ое поле;
- темп-ое поле;
При q=const и λ= const – это ур-е прямой линии.
При λ=f(t). В большинстве случаев это линейная зависимость и можно принять λ=λ0(1+bt);
λ0 – коэф.теплопроводности при t=00С. b – эмпирич-й коэф-т.
подставим λ в ур-е Фурье: 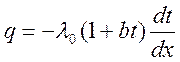 ;
;
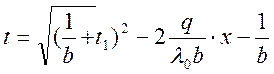 параболическая
зависимость.
параболическая
зависимость.
6.
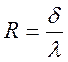 (м2 0С/Вт)
- однослойная стенка;
(м2 0С/Вт)
- однослойная стенка;
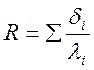 (м2 0С/Вт)
– многослойная стенка;
(м2 0С/Вт)
– многослойная стенка;
λ – коэф.теплопроводности (ккал/м ч 0С).
7.
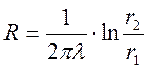 (м 0С/Вт)
линейное термическое сопр-е однослойной цилиндр-й стенки, т.е. терм-ое сопр-е
отнесенное к одному погонному метру длины.
(м 0С/Вт)
линейное термическое сопр-е однослойной цилиндр-й стенки, т.е. терм-ое сопр-е
отнесенное к одному погонному метру длины.
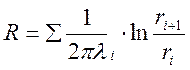 (м 0С/Вт)
термическое сопр-е многослойной цилиндр-й стенки
(м 0С/Вт)
термическое сопр-е многослойной цилиндр-й стенки
λ – коэф.теплопроводности (ккал/м ч 0С).
8.
При решении практических задач пользуются численными методами: метод конечных разностей, гидротепловой и электортопловой аналогии и исп-е цифровых ЭВМ. В аналитических методах широко применяются данные теории подобия.
Метод конечных разностей основана допущении
возможности замены неприрывного процесса изменения темп-ры скачкообразным как в
пространстве, так и во времени. Диф.ур-е теплопроводности заменяются ур-ми в
конечных разностях. 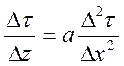 ; Δτ – конечн.приращ-е
темп-ры в 0С; Δz – конечн.приращ-е времени в ч;Δx – толщины эл-х
слоев в м; а – коэф.температуропроводности м2/ч;
; Δτ – конечн.приращ-е
темп-ры в 0С; Δz – конечн.приращ-е времени в ч;Δx – толщины эл-х
слоев в м; а – коэф.температуропроводности м2/ч;
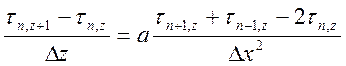 ;
;
Общ. ф-ла для опред-ой темп-ры в любой плоскости ч/з
интервал времени Δz по темп-ам в этой пл-ти и в 2х соседних пл-тях в предыдущий
момент времени z. Т.о. расчет изменения темп-ры во времени сводится к
последовательному вычислению темп-р во всех пл-тях ч/з равные интервалы времени
Δz по ф-ле: 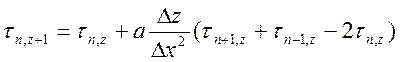 . В частном случае, еслт
подобрать
. В частном случае, еслт
подобрать 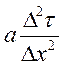 =0.5, то ф-ла примет вид :
=0.5, то ф-ла примет вид : 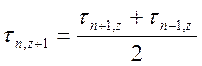 .
.
9.
Процесс конв.теплообмена м/у стенкой и жидкостью представляет собой сложное явление и зависит от условий теплообмена на границе(пограничном слое) и от того на сколько интенсивно теплота подводится или отводится от пограничного слоя, т.е. от условий распределения тепла в ж-ти. Поскольку теплообмен опр-ся не только тепловым, но и гидравл-ми явлениями, то он описывается системой ур-й:
1) Условие теплообмена на границе ж-ть-стенка: 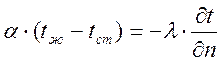 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.