«Математическая викторина»
Цели:
используя полученные на уроках знания, умения и навыки, развивать у детей
интерес к математике; содействовать:
- развитию
математических способностей и логической смекалки;
- развитию
познавательной деятельности учащихся: восприятия, представлений, внимания,
памяти, мышления, речи, воображения;
- развитие
коммуникативных навыков.
Правила игры:
Учащиеся делятся на 3 команды (по рядам). У каждой команды
сначала 0 очков. В каждой выбирается капитан. Он называет того, кто будет
отвечать.
Из первой команды выходит 1 участник, бросает кубик с
цифрами на гранях от 1 до 6. Выпавшая цифра является стоимостью вопроса. Потом
он выбирает карточку с номером вопроса (вопросы находятся у ведущего), который
задается ведущим второй команде. Если вторая команда правильно отвечает на
вопрос, то она получает выпавшее число очков на кубике, в противном случае у
нее вычитается это количество очков, а право ответа предоставляется первой
команде. Очки она получает или теряет аналогичным образом. Если же и первая
команда не отвечает на вопрос, то шанс заработать эти очки появляется у третьей
команды (в случае неправильного ответа она не теряет очки). Затем выходит
участник из второй команды, бросает кубик, и вопрос задается третьей команде, и
т.д.
Также в игре предусмотрены бонусные вопросы, за которые
команда, бросавшая кубик, сразу получает некоторое количество очков, а команда,
которой должен был достаться вопрос, получает количество очков на кубике.
Выигрывает та команда, у которой будет наибольшее
количество очков за отведенное время.
Вопросы:
- Применяя знаки
действий, напишите число 1 тремя двойками. (2-2:2=1)
- Напишите 10
четырьмя тройками. (3х3+3:3=10)
- В доме 100
квартир. Сколько раз на табличках написана цифра 9? (20 раз)
- Какие два целые
числа, если их перемножить, дают столько же, сколько получается от их
сложения? (2х2=4; 2+2=4)
- Какие три целые
числа, если их перемножить, дают столько же, сколько получается от их
сложения? (1, 2, 3; -1, -2 -3; -1, 0, 1)
- Когда два целых
положительных числа, если их сложить, дают больше, чем если их
перемножить? (одно из чисел – единица)
- Чему равно
произведение всех чисел? (0)
- 21 19 30 25 3 12 9
15 6 27 Подберите 3 числа, которые в сумме дадут 50. (19+25+6=50)
- Каковы уменьшаемое
и вычитаемое, если:
_6*5*
*8*4
3856 (6750-3894=2856)
- Найти слагаемые и
сумму по следующим цифрам, из которых некоторые неизвестны:
**45
+5927
78*3
1821* (4445+5927+7843=18215)
- Корабль стоит на
воде со спущенным якорем. Расстояние от иллюминатора до поверхности воды
равно 4 м. За первый час вода поднимается на 0,5 м, а за следующий час –
в 2 раза больше, чем за предыдущий и т.д. За какое время вода достигнет
иллюминатора? (никогда)
- Дано выражение:
1*2*3*4*5*6*7*8*9=20. Поставьте вместо «*» знаки «+» и «-», чтобы
получилось верное равенство, или докажите, что такое невозможно. (это
невозможно, т.к. при выполнении этих действий всегда будет получаться
нечетное число)
- Дано трехзначное
число. Первая цифра этого числа равна 8. Если эту цифру перенести на
последнее место в этом числе, то получится число, на 18 больше начального
числа. Найдите исходное число. (890)
- Шоколадка стоит 10
р., и еще половину шоколадки. Сколько стоит шоколадка? (20 р.)
- Есть две
сковородки. На каждой помещается 1 блин. Надо пожарить три блина с двух
сторон. Каждая сторона блина жарится 1 мин. За какое наименьшее время
можно это сделать? (3 мин.)
- Какие цифры нужно
вписать в прямоугольники?
ࢫࢫࢫ-ࢫࢫ=1. (100-99=1)
- При делении х на 7
получилось
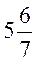. Найдите число х. (41)
- 60 листов книги
имеют толщину 1 см. Какова толщина всех листов книги, если в ней 240
страниц? (2 см)
- 121, 314, 151,
617, 181, … Допишите 2 числа. (920, 212)
- Какое число
делится без остатка на любое целое число, отличное от нуля? (0)
- Найти число, одна
треть которого составляет 12. (36)
- Разделить число
181 пополам так, чтобы в результате получилось 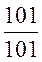1. (
=1)
- Петух, стоя на
одной ноге, весит 5 кг. Сколько он будет весить, если встанет на обе? (5)
- Используя все 10
цифр (каждую из них можно применять только 1 раз), запишите возможно
меньшее число. (1023456789)
- Из двух городов
навстречу друг другу выехали 2 велосипедиста: первый со скоростью 20
км/ч, второй – 15 км/ч. Чему равно расстояние между ними за 2 ч до
встречи. (70 км)
- +3
- +4
- +5
- +6
- +3
- +4
- +5
