Движение в центральном поле. Законы Кеплера (12):
Солнца являются следствиями законов движения Ньютона. Законы движения
небесных тел установлены Кеплером.
I закон: Орбитами всех планет являются эллипсы в одном из фокусов которых находится Солнце.
II закон: Движение каждой планеты происходит так, что радиус-вектор, проведенный из центра Солнца к планете за равные промежутки времени
описывает равные площади.
III закон: Квадраты периодов обращения различных планет вокруг Солнца относятся как кубы больших полуосей.
Второй закон Кеплера является следствием из закона
сохранения момента импульса т.е. 
L=
,
m
=const
Действительно
преобразуем выражение , m=r , m
, 
=
t
.
Выясним смысл векторного произведения.
,
=
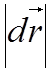
sin(, ).
sin(,)=
;
=2
Обозначая площадь треугольника вектором 
причем вектор этот перпендикулярен,
получим , =2=t =
.
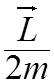
Если 
=const,
m=const то интегрируя получим:
=(
) 
=
.
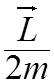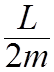
III закон Кеплера легко доказать, если считать, что орбитами всех планет являются окружности. На самом деле для каждой орбиты существует эксцентриситет.
Эксцентриситет – Величина, которая характеризует, на сколько вытянут.
= 0,017; 
=
0,205. Пусть планета имеет массу 
, круговую орбиту 
и период обращения 
;
Вторая
планета – 
, 
, 
.
Для первой планеты
= 
;
= 
=
.
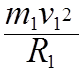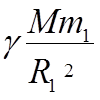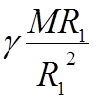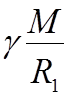Период
обращения планеты = 
= 
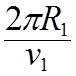
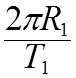, а по аналогии
По аналогии для второй планеты
= 
=
.
= 
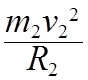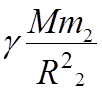
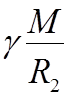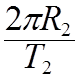. Возведем в квадрат 
= 
;
= 
= 
; 
= 
= 
= 
=
=
.
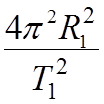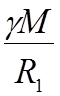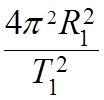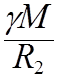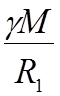
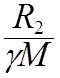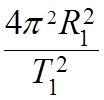
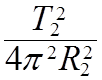
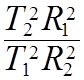
I закон Кеплера:
Вид орбиты определяется начальной скоростью планеты.
1.)
= 
–
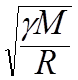круговая орбита.
2.)
Если 
< 
. Тогда в этом случае орбитой является эллипс и Солнце
находится в дальнем фокусе.
3.)
Если > то орбита – Эллипс и Солнце находится в ближнем
фокусе.
4.)
Если 
= 
–
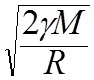орбита – парабола.
5.) >
– Орбита – гипербола; Небесное тело не является
планетой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
