Согласно молекулярной кинетической теории любое тело состоит из мельчайших обособленных частиц называемых молекулами. Эти частицы находятся в беспорядочном, хаотическом движении, интенсивность которого зависит от температуры, такое движение молекул называется тепловым. Состояние термодинамической может быть задано с помощью макроскопических параметров P,V,T, а характеризованное таким способом состояние называется макросостояние.
Для характеристики масс атомов и молекул используют величины относительная атомная масса Ar химического элемента и относительная молекулярная масса Mr. Соотношение определяющее связь между параметрами состояния какого-либо тела называется уравнением состояния этого тела.
Простейшим случаем состояния
некоторой массы газа определяется значением трех параметров f(P,V,T)=0 T=t0C+273(к)
термодинамическая температура. Опытным путем было установлено, что при обычных
условиях параметры состояния газа кислорода и азота удовлетворяют следующим
законам: 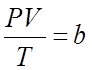 - уравнение Клапейрона, где b – постоянная пропорциональная
массе. Оказалось, что не каждому газу подходит это уравнение. Чем разреженней
газ, тем точнее выполняется уравнение Клапейрона. У разреженного газа молекулы
практически не взаимодействуют между собой, а лишь иногда сталкиваются друг с
другом. Газ, взаимодействиями между молекулами которого можно пренебречь,
называется идеальным. Поэтому уравнение Клапейрона является уравнением
состояния идеального газа. Наиболее близки к идеальному газу гелий и водород.
- уравнение Клапейрона, где b – постоянная пропорциональная
массе. Оказалось, что не каждому газу подходит это уравнение. Чем разреженней
газ, тем точнее выполняется уравнение Клапейрона. У разреженного газа молекулы
практически не взаимодействуют между собой, а лишь иногда сталкиваются друг с
другом. Газ, взаимодействиями между молекулами которого можно пренебречь,
называется идеальным. Поэтому уравнение Клапейрона является уравнением
состояния идеального газа. Наиболее близки к идеальному газу гелий и водород.
Согласно закону Авогадро T=273,15 K, p0=1,013![]() 105Па объем одного
моля любого газа Vm=22,4
105Па объем одного
моля любого газа Vm=22,4![]() 10-3 м3/моль.
Если количество газа равно 1 молю, то постоянная b
одинаковая для всех газов получила название R=8,31
10-3 м3/моль.
Если количество газа равно 1 молю, то постоянная b
одинаковая для всех газов получила название R=8,31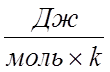 . pVm=RT – уравнение Менделеева. Умножим обе части уравнения на
величину
. pVm=RT – уравнение Менделеева. Умножим обе части уравнения на
величину ![]() , где m –
масса газа,
, где m –
масса газа, ![]() - молярная масса газа.
- молярная масса газа. 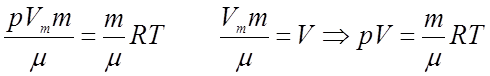 - уравнение Менделеева-Клапейрона.
Умножим и разделим правую часть на Na (Na=6,022
- уравнение Менделеева-Клапейрона.
Умножим и разделим правую часть на Na (Na=6,022![]() 1023
моль-1).
1023
моль-1). 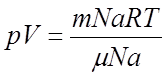 ,
, ![]()
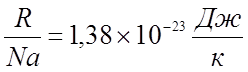 (постоянная Больцмана).
(постоянная Больцмана). ![]() , где
, где 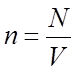 -
число молекул в единице объема.
-
число молекул в единице объема. ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.