Определение диэлектрической проницаемости твердого полярного диэлектрика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ

БЕЛАРУСЬ

Гомельский государственный технический университет

имени П.О.Сухого

Кафедра физики

Лабораторная работа № 2-2

Определение диэлектрической проницаемости твердого полярного диэлектрика.

Выполнил студент гр. ПЭ-14

Некрашевич Г.В

Принял преподаватель

Аксёнкин  Е.А

г. Гомель, 2004

Лабораторная работа №2-2

Определение диэлектрической проницаемости

твердого полярного диэлектрика.

Цель работы: Изучить электрические свойства диэлектриков измерить диэлектрическую проницаемость предлагаемых пластин.

Приборы и принадлежности: составной плоский конденсатор с набором пластин диэлектрика, генератор переменой ЭДС, частотомер, катушка взаимной индуктивности, масштабная линейка, соединительные провода или кабели.

Ход работы.

1.  Собираем конденсатор, измеряем площадь пластин, подключаем к прибору и измеряем частоту все данные вносим в таблицу:

№
1
2
3

Вывод:  Проделав лабораторную работу, мы изучили электрические свойства диэлектриков и измерили диэлектрическую проницаемость пластин.

Теоретическая часть

Каждая поляризованная молекула, как, диполь создает свое электрическое поле, быстро слабеющее при удалении от центра диполя. В не слишком сильных электрических полях деформация молекул невелика и пропорциональна напряженности электрического поля. У неполярного диэлектрика, находящегося во внешнем электрическом поле, все молекулы превращаются в диполи, ориентированные вдоль направления электрического поля. Степень поляризации диэлектрика зависит от его свойств и величины напряженности электрического поля, но не зависит от температуры. Такого рода поляризация имеет место во всех диэлектриках независимо от их агрегатного состояния.

Электрическое поле связанных зарядов поляризованного диэлектрика Е складывается с электрическим            полем Е0 , которое создается свободными зарядами, и результирующее поле Е вызывает поляризацию диэлектрика  где Е=Е+Е.

Причем векторы Р и Е параллельны в том случае, если диэлектрик занимает объем, ограниченный эквипотенциальной поверхностью. Поэтому диэлектрик помещают в плоский конденсатор, заряженный свободными зарядами  q , которые создают электрическое поле Е0  . Направив ось Х параллельно вектору Е получим проекцию Е о, х равную модулю вектора Е. При таком выборе системы отсчета формула связи напряженности и потенциала упрощается до выражения Е о, х=Еmax=dψ/dx откуда dψ=E·dx

Интегрируя обе части этого уравнения от одной пластины до другой, мохно вычислить разность потенциалов между пластинами:.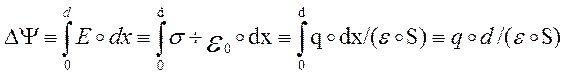

Составив отношение: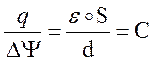 получим формулу емкости плоского вакуумного конденсатора.

;

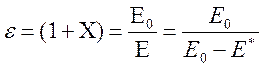Отношение напряженности электрического поля, созданного свободными зарядами в вакууме, к напряженности среднего значения электрического поля в однородном, изотропном диэлектрике при неизменных источниках поля - называется относительной диэлектрической проницаемостью диэлектрика и является основной макроскопической характеристикой диэлектрика. Диэлектрическая проницаемость показывает, во сколько раз электрическое поле свободных зарядов в вакууме сильнее электрического поля тех - же зарядов в диэлектрике.

Из выражения 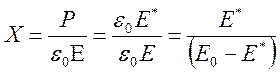 следует, что относительная диэлектрическая восприимчивость показывает, во сколько раз электрическое поле образованное поляризованным веществом сильнее результирующего поля, вызывающего эту поляризацию. Для конденсатора заполненного диэлектриком можно рассчитать емкость:

;

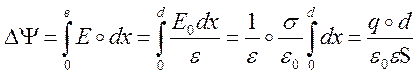Сравнивая последнюю формулу с формулой емкости вакуумного конденсатора, увидим, 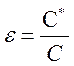 т.е. по   отношению емкости конденсатора заполненного диэлектриком к емкости того – же конденсатора без   диэлектрика при неизменных размерах и формы проводников, можно определить диэлектрическую   проницаемость материала. Поскольку разбираемый конденсатор имеет малую емкость, то измерить ее   можно только очень чувствительными резонансными методами.