Измерение емкости конденсатора методом резонанса

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ

БЕЛАРУСЬ

Гомельский государственный технический университет

имени П.О.Сухого

Кафедра физики

Лабораторная работа № 2-8

Измерение емкости конденсатора методом резонанса.

Выполнил студент гр. Э-13

Колесников П.М.

Принял преподаватель

Курбатова Л.М.

г. Гомель, 2002

Лабораторная работа № 2-8

Измерение емкости конденсатора методом резонанса.

Цель работы: Изучить закон Ома для цепей переменного тока при параллельном соединении реактивных и активных сопротивлений и явление резонанса тока.

Приборы и принадлежности: генератор переменной ЭДС, частотомер, катушка индуктивности, набор конденсаторов, осциллограф, соединительные провода и кабели.

Теоретическая часть

   Резонансные методы измерений являются наиболее простыми и универсальными т.к. позволяют сравнивать с эталонами как индуктивности, так и емкости. Для получения количественных соотношений, нужно использовать закон Ома для цепи переменного тока с параллельным соединением различных элементов: R, C, L. Построим векторную диаграмму тока и напряжения для цепи, в которой к источнику переменной ЭДС параллельно подключены R, L ,C. Поскольку при параллельном соединении сопротивлений напряжение на них одинаково по величине и направлению, то это напряжение совмещается с осью проекций!!!

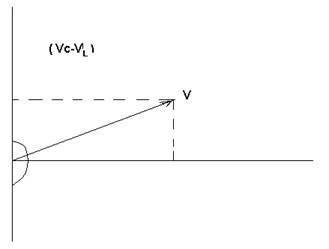
Разные по величине и направлению будут соответствующие токи ILICIR. Поскольку по фазе активный ток совпадает с напряжением на сопротивлении R, то вектор IR направлен по направлению напряжений VR=VL=VC. Емкостной ток IC по фазе па П/2 опережает напряжение VC на конденсаторе, а ток катушки индуктивности IL отстает от напряжения на индуктивности по фазе П/2. На рис. показана векторная диаграмма для случая когда IC>IL, поэтому эти токи противоположны по фазе и результирующий ток равен их разности, и направлен в сторону большего тока. Прибавляя к этому вектору еще и ток IR, получим результирующий ток всей цепи I, величина которого определяется по теореме Пифагора:

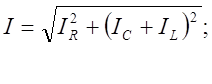
Выразив ток по закону Ома для однородного участка цепи (не одержащего ЭДС), получим:

                                      

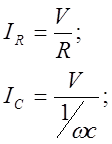
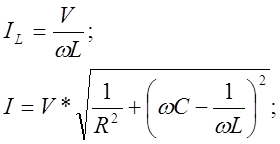
Из этого закона Ома следует, что полное сопротивление цепи при параллельном соединении разных по природе сопротивлений выражается формулой:

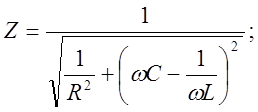
Согласно формуле закона Ома минимальный ток от источника будет при условии что IL=IC и при этом же условии напряжение на параллельной группе будет максимальным. Поэтому реактивные токи катушки и конденсатора будут максимальными и могут существенно превосходить ток источника. Это явление резкого увеличения амплитуды реактивных токов в цепи параллельно включенных катушек и конденсаторов, при совпадении частоты источника с резонансной частотой контура определяется из условия: 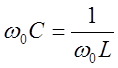 называется резонансом тока.

Ход работы.

1.     Включаем все приборы в сеть, изменяя частоту от 200 кГц до 20 кГц находим значение резонанса, нажав кнопку счет на частотомере измеряем значение частоты все полученные данные вносим в таблицу (R₁=8,2(Ом), R₂=15(Ом), К=0,01):

R	число измерений	1	2	3	4	5	6	7	8	9	10
Rкат		65	55	50	40	35	30	25	20	15	10
		5,66	5,49	5,40	5,32	5,21	5,11	4,92	4,68	4,24	2,92
Rк+R1		60	55	50	40	35	30	25	20	15	10
		5,50	5,47	5,38	5,26	5,17	5,06	4,84	4,71	4,13	2,64
Rк+R2		55	50	45	40	35	30	25	20	15	10
		5,43	5,32	5,25	5,20	5,10	5,00	4,80	4,65	4,10	2,60

2.  Строим график зависимости , ():

Вывод: Изучили явление резонанса тока.