Клетки таблицы в графе «переход», в которых должна содержаться «ошибка», оставлены пустыми и закрашены. Поскольку состояние распознавателя единственно, в записи конфигурации его можно опустить.
Стек лучше заполнять слева направо (для получения естественного порядка правил), поскольку выполняется правосторонний разбор.
Рассмотрим две цепочки: a1=¢aabbb¢; a2=¢aabb¢.
(aabbb^к,{^н,0},
l)├─(abbb^к,{^н,0;
a,2}, l)├─ (bbb^к,{^н,0; a,2;
a,2}, l) ├─ (bb^к, {^н,0; a,2;
a,2; b,3}, l)├─ (bb^к, {^н,0; a,2; a,2;
S,4}, 3l)
├─ (b^к,
{^н,0; a,2;
a,2; S,4; b,3},
3)├─ (b^к,
{^н,0; a,2;
a,2; S,4; S,5}, 33)
├─ (b^к,
{^н,0; a,2;
S,4}, 233)├─ (^к,
{^н,0; a,2;
S,4; b,3}, 233)
├─ (^к, {^н,0; a,2;
S,4; S,5},
3233)├─ (^к, {^н,0; S,1},
23233)
├─ (^к, {^н,0; S¢}, 123233) алгоритм завершён
успешно, цепочка принята.
S¢Þ(1) SÞ(2) aSSÞ(3) aSbÞ(2) aaSSbÞ(3) aaSbbÞ(3) aabbb.
(aabb^к,{^н,0}, l)├─(abb^к,{^н,0; a,2}, l)├─ (bb^к,{^н,0; a,2; a,2}, l)
├─ (b^к, {^н,0; a,2; a,2; b,3}, l)├─ (b^к, {^н,0; a,2; a,2; S,4}, 3l)
├─ (^к, {^н,0; a,2; a,2; S,4; b,3}, 3)├─ (^к, {^н,0; a,2; a,2; S,4; S,5},
33)
├─ (^к, {^н,0; a,2; S,4}, 233)├─ алгоритм завершился с ошибкой.
На практике LR(k)-грамматики для k>1 не применяются: для любой LR(k)-грамматики можно построить эквивалентную ей LR(1)-грамматику, которая работает значительно эффективнее в силу меньших размеров управляющей таблицы.
3.5.2.2 Грамматики предшествования
Ещё один распространенный класс КС-грамматик, для которых возможно построить восходящий распознаватель без возвратов, представляют грамматики предшествования. Распознаватель для них строится также на основе алгоритма «сдвиг-свёртка».
Суть таких грамматик состоит в том, что для каждой упорядоченной пары символов в грамматике устанавливается некоторое отношение, называемое отношением предшествования. В процессе разбора входной цепочки распознаватель сравнивает текущий символ с одним из символов, находящихся на верхушке стека автомата. В процессе сравнения проверяется, какое из отношений предшествования существует между этими двумя символами, и в зависимости от найденного отношения выполняется либо сдвиг, либо свёртка. При отсутствии какого-либо отношения выдается сигнал об ошибке.
Таким образом, задача состоит в том, чтобы определить отношения предшествования между символами грамматики. В случае удачи грамматика может быть отнесена к одному из классов грамматик предшествования.
Существует несколько видов грамматик предшествования. Они различаются по тому, какие отношения предшествования в них определены и между какими типами символов (терминальными или нетерминальными) эти отношения могут быть установлены.
Выделяют следующие типы грамматик предшествования:
§ простого предшествования;
§ расширенного предшествования;
§ слабого предшествования;
§ операторного предшествования.
Наиболее распространены первый и последний типы грамматик.
Для примера рассмотрим грамматики операторного предшествования.
Грамматики, в которых все правила таковы, что в любой правой части никакие два нетерминала не являются смежными, и, следовательно, стоящий между ними терминал можно представить как оператор (хотя и не обязательно в арифметическом смысле), называются операторными грамматиками.
Пусть так же, как и в предыдущем разделе, кроме терминального алфавита VT имеются специальные символы {^н, ^к} (или {├, ┤}), которые ограничивают цепочку слева и справа соответственно.
Будем использовать следующие обозначения цепочек: bÎVNÈ{l} (т.е. нетерминал или пусто), a, g, dÎV* (V=VTÈVN). Определим отношения предшествования {@̇, <×, ×>} на множестве VT È{^к, ^н}:
1. a @b (a имеет такое же старшинство, как b), если A ® aabbg;
2.
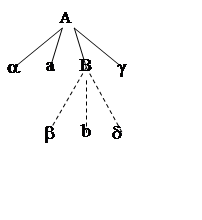
a <× b (a имеет меньшее старшинство,
чем b), если A ® aaBg,
B Þ+
bb d;
Схематичное
представление данного правила показано на первом рисунке.
3.
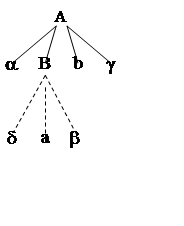
a ×> b
(a имеет большее старшинство, чем b),
если A ® aBbg, B Þ+ dab;
Схематичное представление правила показано на втором рисунке.
4. ^н <× a, если S Þ+ bad;
5. a ×> ^к, если S Þ+ dab.
Если между любыми двумя операторами из VT È{^к, ^н} возможно не более одного такого отношения, то соответствующая операторная грамматика называется грамматикой операторного предшествования.
Пример.
Дана грамматика построения АВ с операциями сложения и умножения и скобками: G({x,+,*,(,)}, {S,T,R}, P, S), где правила P: S ® S+T (1)|T (2), T®T*R (3)|R (4), R®(S) (5)|x (6). Здесь вместо символа x может быть использовано любое целое число.
В соответствии с приведенными выше правилами определения отношений предшествования построим таблицу, в которую занесём отношения между всеми операторами данной грамматики:
|
+ |
* |
( |
) |
x |
^к |
|
|
^н |
<× |
<× |
<× |
<× |
||
|
+ |
×> |
<× |
<× |
×> |
<× |
×> |
|
* |
×> |
×> |
<× |
×> |
<× |
×> |
|
( |
<× |
<× |
<× |
=̇ |
<× |
|
|
) |
×> |
×> |
×> |
×> |
||
|
x |
×> |
×> |
×> |
×> |
Рассмотрим работу алгоритма разбора на базе грамматик ОП.
Цепочка a считается принятой, если за конечное число
шагов произошел переход от начальной конфигурации к заключительной:
(^н a^к,
l,l)├─*(^к, ^н S,m) Þ stop(+).
Алгоритм:
1) Считывающая головка устанавливается на первый символ цепочки a1, в стек заносится ^н, i=1.
2) Верхний символ стека (или ближний к верху стека терминальный символ) сравнивается с ai.
3) Если отношение <× или =̇, то выполняется сдвиг, i++, возврат на шаг 2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.