 Разбор закончен, стек МПА пуст. Если взять последовательность нетерминальных
символов из стека возвратов, получим цепочку номеров альтернатив и можем построить
дерево вывода.
Разбор закончен, стек МПА пуст. Если взять последовательность нетерминальных
символов из стека возвратов, получим цепочку номеров альтернатив и можем построить
дерево вывода.
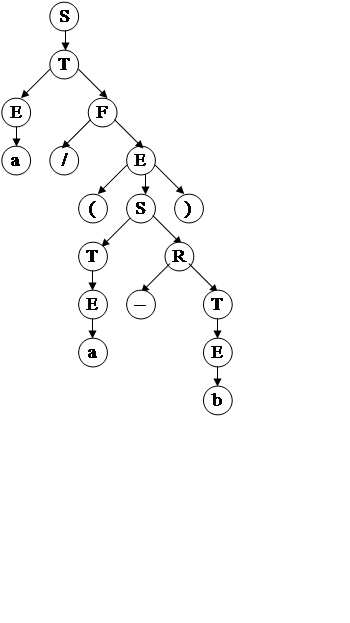
В стеке возврата цепочка S1T2E2aF2/E1(S2T1E2aR2–T1E3b. Удалив терминальные символы, получим S1T2E2F2E1S2T1E2R2T1E3. Тогда цепочка вывода будет иметь вид: SÞTÞEFÞaFÞa/EÞa/(S)Þa/(TR)Þa/(ER)Þa/(aR)Þa/(a–T)Þa/(a–E)Þa/(a–b). Дерево вывода показано на рисунке справа.
Из рассмотренного примера видно, что недостатком алгоритма нисходящего разбора с возвратами является большое время работы. Для разбора достаточно короткой цепочки из 7 символов потребовалось выполнить 70 шагов.
Преимуществом алгоритма является его простота реализации и универсальность.
Сам по себе данный алгоритм не используется в компиляторах, но его основные принципы лежат в основе многих нисходящих распознавателей, строящих левосторонние выводы и работающих без использования возвратов.
3.4.1.2 Распознаватель на основе алгоритма «сдвиг-свёртка»
Этот распознаватель строится на основе расширенного МПА с одним состоянием q: R({q},V,Z,d,q,l,{q}). Автомат распознаёт цепочки КС-языка, задаваемого грамматикой G(VT,VN,P,S). Входной алфавит автомата содержит терминальные символы грамматики V=VT, а алфавит магазинных символов Z=VTÈVN.
Начальная конфигурация автомата (q,a,l), т.е. считывающая головка находится в начале входной цепочки aÎVT*, а стек пуст. Конечная конфигурация автомата (q,l,S), т.е. в стеке находится целевой символ.
Функция перехода строится на основе правил P грамматики G:
1. Если правило (A ® m)ÎP, то (q,A)Îd(q,l,m), AÎVN, mÎ( VTÈVN)*.
2. "aÎVT (q,a)Îd(q,a,l).
Работу автомата можно описать следующим образом. Если на верхушке стека находится цепочка символов m, то ее можно заменить на нетерминальный символ A, если (A ® m)ÎP, не сдвигая считывающую головку автомата. Этот шаг работы алгоритма называется «свёртка». С другой стороны, если считывающая головка обозревает символ входной цепочки a, то его можно поместить в стек, а считывающую головку передвинуть на один символ вправо. Данный шаг называется «сдвиг» или «перенос». Алгоритм называется «сдвиг-свёртка» или «перенос-свёртка».
Данный расширенный автомат строит правосторонние выводы для грамматики G, читает цепочку входных символов слева направо, поэтому строит дерево снизу вверх. Такой распознаватель является восходящим.
Для моделирования такого автомата необходимо, чтобы грамматика не содержала цепных правил и l-правил. Как было рассмотрено ранее, к такому виду может быть приведена любая КС-грамматика, поэтому алгоритм является универсальным.
Рассмотренный автомат имеет больше неоднозначностей, чем распознаватель, основанный на выборе альтернатив. На каждом шаге работы автомата должны быть решены следующие вопросы:
§ что необходимо выполнить – сдвиг или свёртку;
§ если выполнять свёртку, то какую цепочку m выбрать для поиска правил (эта цепочка должна находиться в правой части правил);
§ какое из правил выбрать для свёртки, если в грамматике окажется более одного правила вида (A ® m)ÎP с одинаковой правой частью и различными левыми частями A.
Чтобы промоделировать работу этого расширенного МПА, надо на каждом шаге запоминать все предпринятые действия, чтобы иметь возможность при необходимости вернуться к уже сделанному шагу и проделать все действия иначе. Таким образом должны быть перебраны все возможные варианты.
Рассмотрим один из возможных вариантов реализации алгоритма.
Распознаватель с возвратами на основе алгоритма «сдвиг-свёртка»
Для работы алгоритма используется расширенный МПА, построенный на основе исходной КС-грамматики G(VT,VN,P,S). Все правила из множества P перенумеруем слева направо и сверху вниз в порядке их записи в форме Бэкуса-Наура. Входная цепочка имеет вид a=a1a2…an, ½a½= n, aiÎVT "i.
Аналогично алгоритму нисходящего распознавателя, в рассматриваемом алгоритме используется дополнительное состояние b и стек возвратов L2. Этот стек может содержать номера правил грамматики, использованных для свёртки, если на очередном шаге алгоритма выполнялась свёртка, или 0, если на очередном шаге выполнялся сдвиг.
![]() В
итоге алгоритм работает с двумя стеками, L1
– стек МПА и L2 – стек возвратов, причём первый
содержит цепочку символов, а второй – целые числа от 0 до m,
где m – количество правил грамматики. В цепочку стека L1 символы помещаются справа, а числа в стек L2 – слева.
В
итоге алгоритм работает с двумя стеками, L1
– стек МПА и L2 – стек возвратов, причём первый
содержит цепочку символов, а второй – целые числа от 0 до m,
где m – количество правил грамматики. В цепочку стека L1 символы помещаются справа, а числа в стек L2 – слева.
Состояние алгоритма на каждом шаге определяется четырьмя параметрами: (Q,i,L1,L2), где Q – текущее состояние автомата (q или b), i – положение считывающей головки во входной цепочке a (1 < i £ n+1), L1 и L2 – содержимое стеков.
Начальным состоянием алгоритма является (q,1,l,l). Алгоритм начинает работу с начального состояния и циклически выполняет 5 шагов до тех пор, пока не перейдёт в конечное состояние или не обнаружит ошибку. Конечное состояние алгоритма (q,n+1,S,g).
Алгоритм выполняет циклически следующие шаги:
Шаг 1 («Попытка свертки»): (q, i, mb, g) ® (q, i, mA, jg), где bÎ(VNÈVT)*, g – содержимое стека возвратов L2, если (A ® b)ÎP – первое из всех возможных правил из множества P с номером j для подцепочки b, причём оно является первым подходящим правилом для цепочки mb, для которой правило вида A ® b существует (заменяем цепочку в стеке МПА на нетерминал – «сворачиваем» её, а в стек возврата записываем номер использованного правила). Если удалось выполнить свёртку, то возвращаемся к шагу 1, иначе переходим к шагу 2.
Шаг 2 («Перенос-сдвиг»): Если i < n+1, то (q, i, m, g) ® (q, i+1, mai, 0g), где aiÎVT. Если i = n+1, то идти дальше, иначе перейти к шагу 1.
Шаг 3 («Завершение»): Если состояние алгоритма (q, n+1, S, g), то разбор завершён и алгоритм заканчивает работу, иначе перейти к шагу 4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.