Информатика и выч. техника \ Теория языков программирования и методы трансляции

Контекстно-свободные языки. Свойства и распознаватели КС-языков. Преобразование КС-грамматик. КС-грамматики в нормальной форме, страница 11

Шаг 4 («Переход к возврату»): (q, n+1, m, g) ® (b, n+1, m, g).

Шаг 5 («Возврат»): При возврате возможны следующие варианты:

1)  Если исходное состояние алгоритма (b, i, mA, jg) (j>0):

§  Перейти (b, i, mA, jg) ® (q, i, m¢B, kg), если (A ® b)ÎP – это правило с номером j и существует правило (B ® b¢)ÎP с номером k, k>j, такое, что mb=m¢b¢, после чего вернуться к шагу 1.

§  Перейти (b, i, mA, jg) ® (b, n+1, mb, g), если i=n+1, (A ® b)ÎP – это правило с номером j и не существует других правил из множества P с номером k, k>j, таких, что их правая часть является суффиксом цепочки mb, после этого вернуться к шагу 5.

§  Перейти (b, i, mA, jg) ® (q, i+1, mbai, 0g), где aiÎVT, если i¹n+1, (A ® b)ÎP – это правило с номером j и не существует других правил из множества P с номером k>j, таких, что их правая часть является правой подцепочкой из цепочки mb, после этого перейти к шагу 1.

§  Иначе сигнализировать об ошибке и прекратить выполнение.

2)  Если исходное состояние алгоритма (b, i, ma, 0g), aÎVT, то если i>1, тогда перейти в следующее состояние (b, i–1, m, g) и вернуться к шагу 5, иначе сигнализировать об ошибке и прекратить выполнение алгоритма.

При успешном завершении алгоритма на основе содержимого стека возврата можно построить цепочку вывода. Для этого достаточно удалить из стека все 0 и будет получена последовательность номеров правил, используемых при выводе цепочки.

Пример: Пусть дана грамматика для арифметических выражений:

G ({+,–,/,*,a,b,(,)}, {S,T,E}, P, S), где правила P имеют вид:

S ® S+T [1]½S–T [2]½T*E [3]½T/E [4]½(S) [5]½a [6]½b [7]

T ® T*E [8]½T/E [9]½(S) [10]½a [11]½b [12]

E ® (S) [13]½a [14]½b [15].

Рассмотрим разбор двух цепочек: ‘a+b’ и ‘a/(a–b)’.

1) (q,1,l,l) |¾(2) (q,2,a,[0,l]) |¾(1) (q,2,S,[6,0]) |¾(2) (q,3,S+,[0,6,0]) |¾(2) (q,4,S+b,[0,0,6,0]) |¾(1) (q,4,S+S,[7,0,0,6,0]) |¾(4) (b,4,S+S,[7,0,0,6,0]) |¾(5) (q,4,S+T,[12,0,0,6,0]) |¾(1) (q,4,S,[1,12,0,0,6,0]) |¾(3) stop

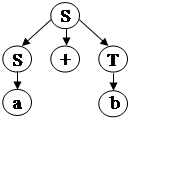
Алгоритм успешно завершён, в стеке возврата содержатся номера правил, которые участвовали в выводе цепочки: L2 = [1,12,0,0,6,0] = [1,12,6]. Þ цепочка  вывода имеет вид S Þ S+T Þ S+b Þ a+b. Построим дерево вывода.

2) ‘a/(a–b)’:

(q,1,l,l)

|¾(2)

(q,2,a,[0,l])

перенесли символ ”a”

|¾(1)

(q,2,S,[6,0])

выполнили свертку

|¾(2)

(q,3,S/,[0,6,0])

перенесли символ ”/”

|¾(2)

(q,4,S/(,[0,0,6,0])

перенесли символ ”(”

|¾(2)

(q,5,S/(a,[0,0,0,6,0])

перенесли символ ”a”

|¾(1)

(q,5,S/(S,[6,0,0,0,6,0])

выполнили свертку по №6

|¾(2)

(q,6,S/(S–,[0,6,0,0,0,6,0])

перенесли символ ”–”

|¾(2)

(q,7,S/(S–b,[0,0,6,0,0,0,6,0])

перенесли символ ”b”

|¾(1)

(q,7,S/(S–S,[7,0,0,6,0,0,0,6,0])

выполнили свёртку по №7

|¾(2)

(q,8,S/(S–S),[0,7,0,0,6,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(S–S),[0,7,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(S–S,[7,0,0,6,0,0,0,6,0])

выполнили возврат

|¾(5)

(q,7,S/(S–T,[12,0,0,6,0,0,0,6,0])

заменили на другое правило

|¾(1)

(q,7,S/(S,[2,12,0,0,6,0,0,0,6,0])

выполнили свёртку S–T по №2

|¾(2)

(q,8,S/(S),[0,2,12,0,0,6,0,0,0,6,0])

перенесли символ ”)”

|¾(1)

(q,8,S/S,[5,0,2,12,0,0,6,0,0,0,6,0])

выполнили свёртку по №5

|¾(4)

(b,8,S/S,[5,0,2,12,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5.1.1)

(q,8,S/T,[10,0,2,12,0,0,6,0,0,0,6,0])

заменили на другое правило

|¾(4)

(b,8,S/T,[10,0,2,12,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5.1.1)

(q,8,S/E,[13,0,2,12,0,0,6,0,0,0,6,0])

заменили на другое правило

|¾(4)

(b,8,S/E,[13,0,2,12,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5.1.2)

(b,8,S/(S),[0,2,12,0,0,6,0,0,0,6,0])

вернулись назад по 13 правилу

|¾(5.2)

(b,7,S/(S,[2,12,0,0,6,0,0,0,6,0])

возврат по символу ”)”

|¾(5.1.3)

(q,8,S/(S–T),[0,12,0,0,6,0,0,0,6,0])

развернули пр.2, сдвинули ”)”

|¾(4)

(b,8,S/(S–T),[0,12,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5.2)

(b,7,S/(S–T,[12,0,0,6,0,0,0,6,0])

вернулись назад по 2 правилу

|¾(5.1.1)

(q,7,S/(S–E,[15,0,0,6,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,8,S/(S–E),[0,15,0,0,6,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(S–E),[0,15,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5.2)

(b,7,S/(S–E,[15,0,0,6,0,0,0,6,0])

возврат по символу ”)”

|¾(5.1.3)

(q,8,S/(S–b),[0,0,0,6,0,0,0,6,0])

вернулись по 15 прав., сдвиг

|¾(4)

(b,8,S/(S–b),[0,0,0,6,0,0,0,6,0])

перешли к возврату

|¾(5.2)

(b,7,S/(S–b,[0,0,6,0,0,0,6,0])

возврат по символу ”)”

|¾(5.2)

(b,6,S/(S–,[0,6,0,0,0,6,0])

возврат по символу ”b”

|¾(5.2)

(b,5,S/(S,[6,0,0,0,6,0])

возврат по символу ”–”

|¾(5.1.1)

(q,5,S/(T,[11,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,6,S/(T–,[0,11,0,0,0,6,0])

перенесли символ ”–”

|¾(2)

(q,7,S/(T–b,[0,0,11,0,0,0,6,0])

перенесли символ ”b”

|¾(1)

(q,7,S/(T–S,[7,0,0,11,0,0,0,6,0])

выполнили свёртку по №7

|¾(2)

(q,8,S/(T–S),[0,7,0,0,11,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(T–S),[0,7,0,0,11,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(T–S,[7,0,0,11,0,0,0,6,0])

возврат по символу ”)”

|¾(5)

(q,7,S/(T–T,[12,0,0,11,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,8,S/(T–T),[0,12,0,0,11,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(T–T),[0,12,0,0,11,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(T–T,[12,0,0,11,0,0,0,6,0])

возврат по символу ”)”

|¾(5)

(q,7,S/(T–E,[15,0,0,11,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,8,S/(T–E),[0,15,0,0,11,0,0,0,6,0])

перенесли символ ”)”

|¾(5)

(b,8,S/(T–E),[0,15,0,0,11,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(T–E,[15,0,0,11,0,0,0,6,0])

возврат по символу ”)”

|¾(5.1.3)

(q,8,S/(T–b),[0,0,0,11,0,0,0,6,0])

|¾(4)

(b,8,S/(T–b),[0,0,0,11,0,0,0,6,0])

|¾(5)

(b,7,S/(T–b,[0,0,11,0,0,0,6,0])

возврат по символу ”)”

|¾(5)

(b,6,S/(T–,[0,11,0,0,0,6,0])

возврат по символу ”b”

|¾(5)

(b,5,S/(T,[11,0,0,0,6,0])

возврат по символу ”–”

|¾(5)

(q,5,S/(E,[14,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,6,S/(E–,[0,14,0,0,0,6,0])

перенесли символ ”–”

|¾(2)

(q,7,S/(E–b,[0,0,14,0,0,0,6,0])

перенесли символ ”b”

|¾(1)

(q,7,S/(E–S,[7,0,0,14,0,0,0,6,0])

выполнили свёртку по №7

|¾(2)

(q,8,S/(E–S),[0,7,0,0,14,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(E–S),[0,7,0,0,14,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(E–S,[7,0,0,14,0,0,0,6,0])

возврат по символу ”)”

|¾(5)

(q,7,S/(E–T,[12,0,0,14,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,8,S/(E–T),[0,12,0,0,14,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(E–T),[0,12,0,0,14,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(E–T,[12,0,0,14,0,0,0,6,0])

возврат по символу ”)”

|¾(5)

(q,7,S/(E–E,[15,0,0,14,0,0,0,6,0])

заменили на другое правило

|¾(2)

(q,8,S/(E–E),[0,15,0,0,14,0,0,0,6,0])

перенесли символ ”)”

|¾(4)

(b,8,S/(E–E),[0,15,0,0,14,0,0,0,6,0])

перешли к возврату

|¾(5)

(b,7,S/(E–E,[15,0,0,14,0,0,0,6,0])

возврат по символу ”)”

|¾(5.1.3)

(q,8,S/(E–b),[0,0,0,14,0,0,0,6,0])

|¾(4)

(b,8,S/(E–b),[0,0,0,14,0,0,0,6,0])

|¾(5)

(b,7,S/(E–b,[0,0,14,0,0,0,6,0])

возврат по символу ”)”

|¾(5)

(b,6,S/(E–,[0,14,0,0,0,6,0])

возврат по символу ”b”

|¾(5)

(b,5,S/(E,[14,0,0,0,6,0])

возврат по символу ”–”

|¾(5)

(q,6,S/(a–,[0,0,0,0,6,0])

дальше снова с b и свёртки…

…17 шагов…

|¾(5)

(b,5,S/(a,[0,0,0,6,0])

больше нет правил с ‘a’ справа

|¾(5)

(b,4,S/(,[0,0,6,0])

возврат по символу ”(”

|¾(5)

(b,3,S/,[0,6,0])

возврат по символу ”/”

|¾(5)

(b,2,S,[6,0])

вернулись назад по 6 правилу

|¾(5)

(q,2,T,[11,0])

заменили на другое правило

|¾(2)

(q,3,T/,[0,11,0])

перенесли символ ”/”

|¾(2)

(q,4,T/(,[0,0,11,0])

перенесли символ ”(”

|¾(2)

(q,5,T/(a,[0,0,0,11,0])

перенесли символ ”a”

|¾(1)

(q,5,T/(S,[6,0,0,0,11,0])

выполнили свёртку по №6

|¾(2)

(q,6,T/(S–,[0,6,0,0,0,11,0])

перенесли символ ”–”

|¾(2)

(q,7,T/(S–b,[0,0,6,0,0,0,11,0])

перенесли символ ”b”

|¾(1)

(q,7,T/(S–S,[7,0,0,6,0,0,0,11,0])

выполнили свёртку по №7

|¾(2)

(q,8,T/(S–S),[0,7,0,0,6,0,0,0,11,0])

перенесли символ ”)”

|¾(4)

(b,8,T/(S–S),[0,7,0,0,6,0,0,0,11,0])

перешли к возврату

|¾(5)

(b,7,T/(S–S,[7,0,0,6,0,0,0,11,0])

возврат по символу ”)”

|¾(5)

(q,7,T/(S–T,[12,0,0,6,0,0,0,11,0])

заменили на другое правило

|¾(1)

(q,7,T/(S,[2,12,0,0,6,0,0,0,11,0])

выполнили свёртку по №2

|¾(2)

(q,8,T/(S),[0,2,12,0,0,6,0,0,0,11,0])

перенесли символ ”)”

|¾(1)

(q,8,T/S,[5,0,2,12,0,0,6,0,0,0,11,0])

выполнили свёртку по №5

|¾(4)

(b,8,T/S,[5,0,2,12,0,0,6,0,0,0,11,0])

перешли к возврату

|¾(5)

(q,8,T/T,[10,0,2,12,0,0,6,0,0,0,11,0])

заменили на другое правило

|¾(4)

(b,8,T/T,[10,0,2,12,0,0,6,0,0,0,11,0])

перешли к возврату

|¾(5)

(q,8,T/E,[13,0,2,12,0,0,6,0,0,0,11,0])

заменили на другое правило

|¾(1)

(q,8,S,[4,13,0,2,12,0,0,6,0,0,0,11,0])

выполнили свёртку по №4

|¾(3)

stop +
Скачать файл