Результаты сведем в таблицу.
Таблица 3.
Критическая длина конвейера
|
Кратность периода возмущения |
Скорость распространения волны вдоль ветвей цепи, С (м/с) |
Критическая длина Lкр(м) при |
||
|
Грузовой, Cг |
Порожняковый, Сп |
Холостом ходе |
Работе с расчетной нагрузкой |
|
|
1 |
1339,007 |
2069,62 |
62,49 |
64,7 |
|
3 |
1339,007 |
2069,62 |
187,5 |
194,03 |
|
5 |
1339,007 |
2069,62 |
312,499 |
323,4 |
|
7 |
1339,007 |
2069,62 |
437,5 |
452,73 |
Пример расчета:
![]()
![]()
ЛИТЕРАТУРА
1, Транспорт
на горных предприятиях (Под общей ред. проф.
Б.А. Кузнецова. - М.: Недра, 1976 - 552 с.
2. Пухов Ю.С. Транспортные машины. - М.: Недра, 1987. -232с
3 Шахмейстер Л.Г., Солод Г.И. Подземные конвейерные установки. - М.: Недра, 1976. - 432 с.
4. Григорьев В.Н., Дьяков В.А., Пухов Ю.С. Транспортные машины для подземных разработок. - М.: Недра, 1984. - 383 с.
5. Транспортные машины горнорудных предприятий. - М.: Недра 1985. - 336 с.
6. Машины и оборудование для угольных шахт: Справочник /Под ред. В.Н. Хорина. - М.: Недра, 1987. - 424 с.
7. Подземный транспорт шахт и рудников: Справочник /Под общей ред. Г.Я. Пейсаховича, Н.П. Ремизова. - М.: Недра, 1985. -
- 565 с.
8. Проходчик горных выработок: Справочник рабочего /Под ред А.И. Петрова. - М.: Недра, 1991. - 646 с.
9. Поляков А.С, Штокман И.Г. Основы теории и расчёты рудничных транспортных установок. М.: Госгортехиздат, 1962. -491 с.
10. РТМ 24.076.07. Конвейеры шахтные скребковые передвижные Тяговый расчет. Методика. Изд. завода "Свет шахтера" - ИГД им. А.А. Скочинского. Харьков, 1972. - 64 с.
11. Штокман И.Г. Динамика тяговых цепей рудничных конвейеров. - М.: Углетехиздат, 1959. - 288 с.
12. Проектирование и конструирование транспортных машин и комплексов: Учеб. для вузов (Под ред. И.Г. Штокмана. - 2-е изд. , перераб. и доп. - М.: Недра, 1986, 392 с.
13. Леусенко А.Б., Высоцкий Г.В., Эйдерман Б.А. Скребковые конвейеры: Справочное пособие. - М.: Недра, 1993. - 221 с.
ВОПРОСЫ
К защите лабораторной работы: «Тяговый расчет скребкового конвейера методом построения диаграмм натяжения»:
1. Что следует понимать под символом «τ»?
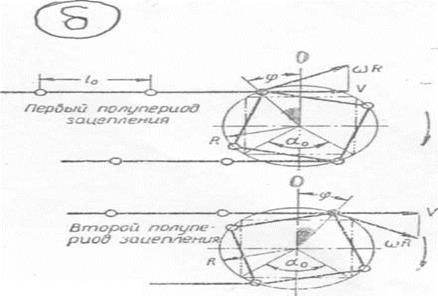
2. Покажите на рисунке «б» точку, соответствующую моменту времени начала зацепления зубца звездочки с шарниром цепи?
3. Физический смысл точек: 1;2;3;4 и т.д на рисунке «в»?
4. Поясните, почему ускорение в момент времени «τ» равно нулю (ри. В)?
5. Покажите формулу, описывающую изменение значения скорости Vц за время 2τ?
6. Поясните, почему на графике ускорения имеются значения «+» и «-» (рис.В)?
7. Покажите соответствующие формулы, по которым изменяются значения ускорений с «+» и с «-», следуя графикам (рис.В.)?
8. Покажите точки начало и конец зацепления одного зубца звездочки с шарниром цепи (рис. Б)?
9. Располагая формулами изменения скорости Vц, получить формулы:
![]()
![]()
10. Покажите аналитически, располагая характером изменения скорости цепи за время 2𝜏, что имеются в области с ускорением «+» и «-»?
11. Вывести формулу, выражающую значение amax через скорость цепи Vц число зубцов звездочки?
Для защиты лабораторной работы
Для защиты лабораторной работы
|
|
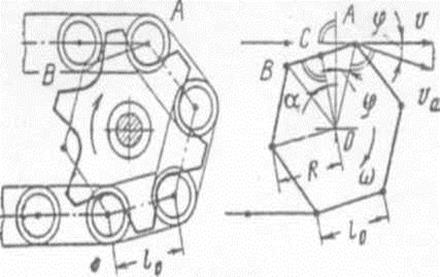
Линейная скорость центров шарниров цепи v (м/с) при огибании цепью —звдздочки: v = 𝜔∙R, где 𝜔 - угловая скорость ведущей звездочки (с-1); R - радиус начальной окружности звездочки (м).
Скорость движения тяговой цепи v (м/с): v = 𝜔∙R∙cos 𝜑. где 𝜑 - угловое
перемещение звездочки (рад), изменяющееся за период 2τ зацепления одного зубца звездочки, от -𝛼. вначале зацепления до +𝛼 в конце.
Ускорение цепи α(м/с2):
![]()
![]()
![]()
![]()
|
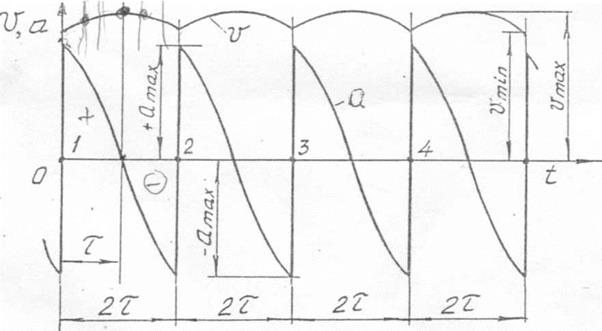
Рис. 5. Графики изменения скорости цепи и ускорения в точках набегания на ведущую звездочку и сбегания с нее: V - скорость цепи (м/с); 𝛼 - ускорение цепи (м/с); t - время (с); 2τ - период зацепления одного зубца звездочки с шарниром цепи (с); τ - полупериод зацепления (с); 1,2,3,4 - точки момента времени начала зацепления, в которые происходит динамический удар
1.
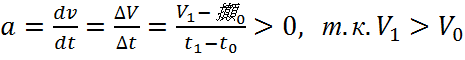
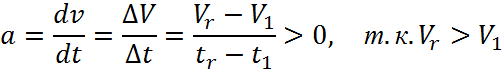
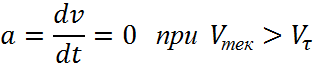
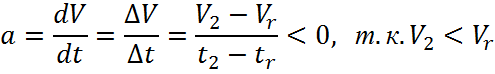
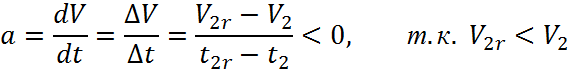
2. (∙) 1; (∙) 2.
3. φ=-φ
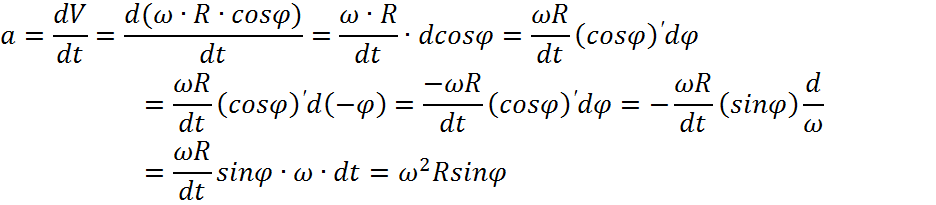
4. 𝜑=+𝜑
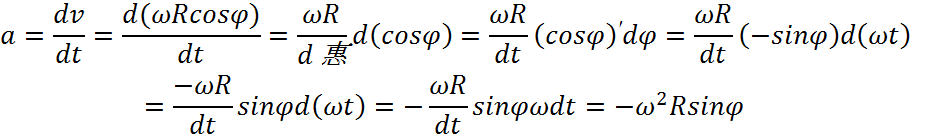
5.
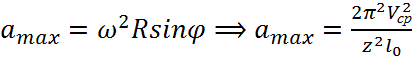
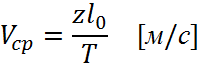
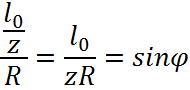
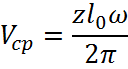
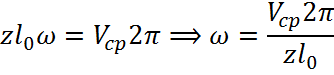
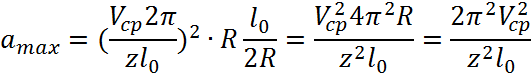

|
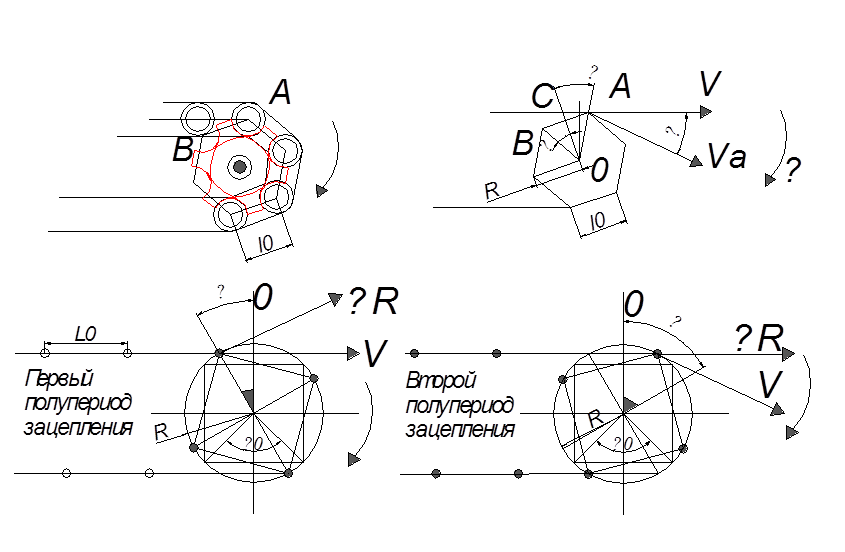
Линейная скорость центров шарниров цепи v (м/с) при огибании цепью —звдздочки: v = 𝜔∙R, где 𝜔 - угловая скорость ведущей звездочки (с-1); R - радиус начальной окружности звездочки (м).
Скорость движения тяговой цепи v (м/с): v = 𝜔∙R∙cos 𝜑. где 𝜑 – угловое перемещение звездочки (рад), изменяющееся за период 2τ зацепления одного зубца звездочки, от -𝛼. вначале зацепления до +𝛼 в конце.
Ускорение цепи α(м/с2):
![]()
![]()
![]()
![]()
|

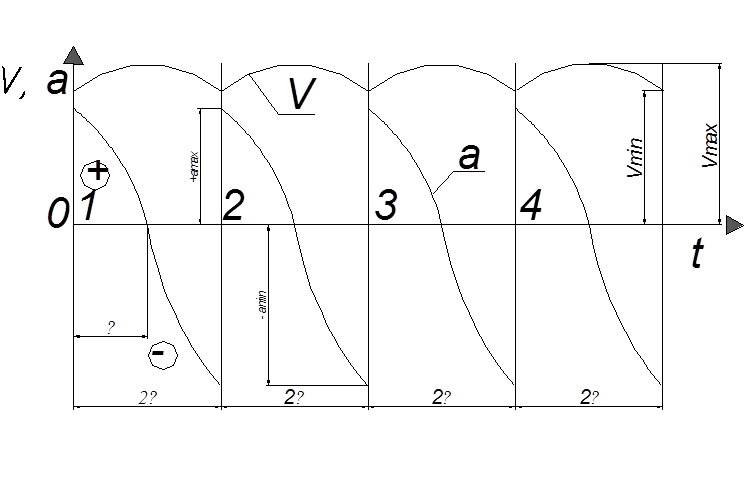
Рис. 5. Графики изменения скорости цепи и ускорения в точках набегания на ведущую звездочку и сбегания с нее: V - скорость цепи (м/с); 𝛼 - ускорение цепи (м/с); t - время (с); 2τ - период зацепления одного зубца звездочки с шарниром цепи (с); τ - полупериод зацепления (с); 1,2,3,4 - точки момента времени начала зацепления, в которых происходит динамический удар
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.