Доминирующей тенденцией развития современного приборостроения является широкое внедрение цифровой обработки сигналов на основе компьютеризации. При этом существует два направления: одно из них основано на использовании микропроцессоров в составе цифровых измерительных средств (ЦИС), а другое направление связано с созданием так называемых компьютерных измерительных устройств, которые представляют сочетание персонального компьютера с разнообразными типовыми платами, размещаемые в его корпусе в специально отведенных посадочных местах. Применение таких ЦИС обусловлено тем что в них значительно сокращают или исключают полностью аналоговые функциональные операции над сигналами, заменяя их цифровой обработкой кодов мгновенных значений сигналов, получаемых с помощью АЦП.
Обобщенная математическая модель цифровой обработки сигналов (ЦОС) имеет следующий вид:
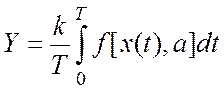 , (1)
, (1)
где У – результат измерения;
x(t) – вектор (совокупность) входных сигналов ЦИС;
a – вектор параметров ЦИС, определяющих алгоритмы обработки;
Т – время измерения;
k – коэффициент передачи ЦИС.
Функция f[x(t),a] полностью описывает все основные алгоритмы, назовем ее алгоритмической (АФ).
ЦОС приводит к методическим
погрешностям дискретизации и квантования, к которым добавляются различного рода
инструментальные погрешности, в том числе вносимые помехами. Поэтому результат
измерения ![]() на выходе ЦИС отличается от точного
значения Y может быть записан
в виде
на выходе ЦИС отличается от точного
значения Y может быть записан
в виде
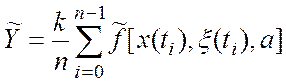 (2)
(2)
где n – число отсчетов мгновенных значений сигнала x(t);
![]() –
значения алгоритмической функции
–
значения алгоритмической функции ![]() в точках отсчета
в точках отсчета ![]() , искаженные помехами и погрешностями
(реальная алгоритмическая функция);
, искаженные помехами и погрешностями
(реальная алгоритмическая функция);
![]() –
вектор погрешностей (кроме погрешности дискретизации), а также различного рода
помех в точках отсчета
–
вектор погрешностей (кроме погрешности дискретизации), а также различного рода
помех в точках отсчета ![]() .
.
Реальная обобщенная модель ЦОС,
определяемая формулой (2), используется для оценки погрешностей ЦИС, которые
сведены в четыре группы: погрешности дискретизации (за счет перехода от точной
формулы (1) к приближенной формуле (2) – формуле прямоугольников); погрешность
квантования АЦП; динамические погрешности (обусловленные инерционностью входных
цепей ЦИС и смещением точек дискретизации ![]() ,
а также апертурная погрешность, или погрешность датирования); погрешности,
вносимые помехами, в том числе инструментальными погрешностями.
,
а также апертурная погрешность, или погрешность датирования); погрешности,
вносимые помехами, в том числе инструментальными погрешностями.
В общем случае результирующая погрешность ЦИС может сложно зависеть от отдельных составляющих, однако применительно к средствам измерительной техники (СИТ), задача оценки этой погрешности значительно упрощается. Любое СИТ выполняется так, чтобы его абсолютная погрешность
![]() (3)
(3)
была мала по сравнению с измеряемой
величиной Y. Это означает, что и отдельные составляющие
погрешности ![]() должны быть малы. Если к тому же
различные составляющие
должны быть малы. Если к тому же
различные составляющие ![]() независимы, то имеет место
принцип суперпозиции погрешностей, состоящие в том, что результирующая
погрешность
независимы, то имеет место
принцип суперпозиции погрешностей, состоящие в том, что результирующая
погрешность ![]() есть сумма отдельных составляющих,
каждая из которых может вычисляться при условии отсутствия остальных
составляющих, то есть предполагается их равенство нулю.
есть сумма отдельных составляющих,
каждая из которых может вычисляться при условии отсутствия остальных
составляющих, то есть предполагается их равенство нулю.
Подставляя в формулу (3) выражения (1) и (2), имеем
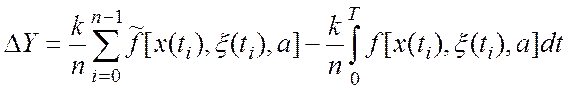 ,
,
где ![]()
![]() при
при ![]() ,
то есть идеальная
,
то есть идеальная ![]() и реальная
и реальная ![]() АФ равны в отсутствие помех (и
погрешностей) исключая погрешность дискретизации, которая в реальной АФ не
учитывается. Погрешность дискретизации является специфичной, и для ее оценки
могут быть использованы временной метод, спектральный метод и метод, основанный
на коэффициенте гармоник. Применение теоремы Котельника для ЦОС в измерительной
технике неприемлемо, так как она не позволяет оценить погрешность
дискретизации. Представим остальные погрешности в виде
АФ равны в отсутствие помех (и
погрешностей) исключая погрешность дискретизации, которая в реальной АФ не
учитывается. Погрешность дискретизации является специфичной, и для ее оценки
могут быть использованы временной метод, спектральный метод и метод, основанный
на коэффициенте гармоник. Применение теоремы Котельника для ЦОС в измерительной
технике неприемлемо, так как она не позволяет оценить погрешность
дискретизации. Представим остальные погрешности в виде
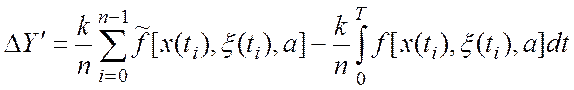 .
.
Используя допущения о малости всех
составляющих погрешности ЦИС, реальную АФ ![]() можно
разложить в ряд Тейлора и сохранить в нем только члены наинизшего порядка,
приводящее в дальнейшем к ненулевой оценке погрешности. Члены ряда более
высокого порядка будут равны по сравнению с указанными, если
можно
разложить в ряд Тейлора и сохранить в нем только члены наинизшего порядка,
приводящее в дальнейшем к ненулевой оценке погрешности. Члены ряда более
высокого порядка будут равны по сравнению с указанными, если ![]() не попадает в окрестность особой
точки АФ. Учет членов ряда более высокого порядка не имеет смысла, так как при
малых погрешностях он приводит только к такому незначительному уточнению
погрешности ЦИС, которая лежит за пределами потребностей практики.
не попадает в окрестность особой
точки АФ. Учет членов ряда более высокого порядка не имеет смысла, так как при
малых погрешностях он приводит только к такому незначительному уточнению
погрешности ЦИС, которая лежит за пределами потребностей практики.
Если к ненулевой оценки погрешности
приводят члены разложения первого порядка малости, то для оценки погрешности ![]() получим
получим
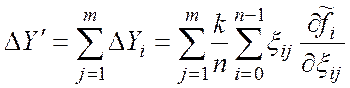 (4)
(4)
где 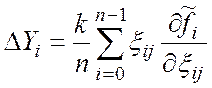 ;
;
j – порядковый номер составляющей погрешности ЦИС;
![]() –
значения отдельных составляющих погрешности ЦИС в точках отсчета
–
значения отдельных составляющих погрешности ЦИС в точках отсчета ![]() ;
;
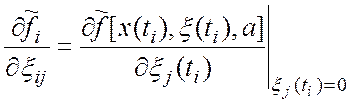 –
значения производных реальной АФ по составляющим погрешности
–
значения производных реальной АФ по составляющим погрешности ![]() в точках отсчета
в точках отсчета ![]() , вычисленных при
, вычисленных при ![]() .
.
Формула (4) представляет собой
запись принципа суперпозиции погрешностей ![]() .
.
Ее математическое ожидание,
представляющее систематическую составляющую погрешности ![]() ,
в общем виде определяется соотношением
,
в общем виде определяется соотношением
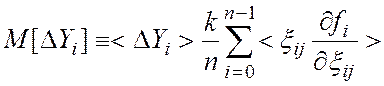 ,
,
где скобки ![]() означают
усреднение по ансамблю случайные величин.
означают
усреднение по ансамблю случайные величин.
Если математическое ожидание ![]() составляющей погрешности
составляющей погрешности ![]() не коррелированной с сигналом и
имеющей равное нулю математическое ожидание
не коррелированной с сигналом и
имеющей равное нулю математическое ожидание ![]() ,
в первом порядке малости
,
в первом порядке малости ![]() =0, то в
разложением в ряд Тейлора АФ
=0, то в
разложением в ряд Тейлора АФ ![]() следует учесть члены
второго порядка малости, обусловленные произведением перекрестных членов ряда.
Тогда
следует учесть члены
второго порядка малости, обусловленные произведением перекрестных членов ряда.
Тогда
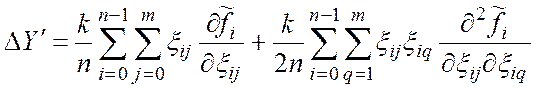 ; (5)
; (5)
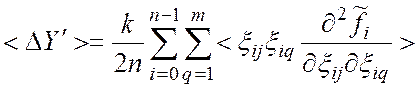 . (6)
. (6)
Используя формулу (4), найдем дисперсию
погрешности ![]() :
:
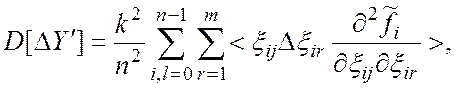 (7)
(7)
где ![]() –
разности между значением погрешности и ее математическим ожиданием.
–
разности между значением погрешности и ее математическим ожиданием.
Варианты погрешностей
1. Если
составляющие погрешностей ЦИС некоррелированы с измерительным сигналом ![]() и между собой, что характерно для
погрешностей различного происхождения, то из выражений (5)-(7) имеем
и между собой, что характерно для
погрешностей различного происхождения, то из выражений (5)-(7) имеем
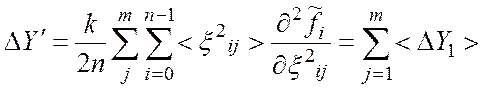 , (8)
, (8)
где 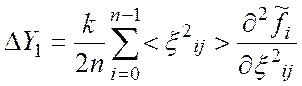 ; (9)
; (9)
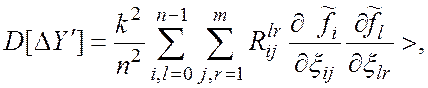 (10)
(10)
(здесь ![]() –
матрица корреляций между i-й составляющей погрешности в
момент
–
матрица корреляций между i-й составляющей погрешности в
момент ![]() и r-й
составляющей погрешности в момент отсчета
и r-й
составляющей погрешности в момент отсчета ![]() ).
).
При условии, что различные составляющие погрешности не коррелированны, из выражения (10) получим
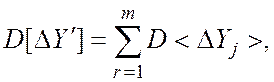
где 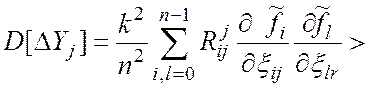 ; (12)
; (12)
![]() .
.
Если погрешности в разных точках отсчета не коррелированны, то
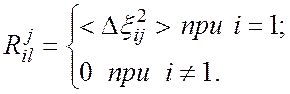
Тогда из формулы (12) для дисперсии
погрешности ![]() имеем
имеем
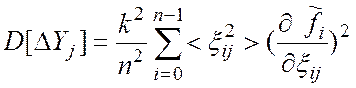 . (13)
. (13)
Как видно из соотношений (8), (11), для данного варианта имеет место «принцип суперпозиции» для математических ожиданий и дисперсий погрешностей.
2. Если
погрешность ![]() представляет стационарный случайный процесс,
то выражения (9), (13) принимают вид
представляет стационарный случайный процесс,
то выражения (9), (13) принимают вид
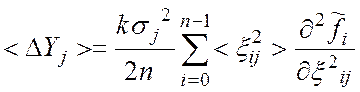 ;
;
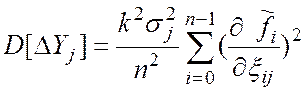 .
.
где ![]() –
дисперсия (соответственно
–
дисперсия (соответственно ![]() – СКО) j-й составляющей погрешности.
– СКО) j-й составляющей погрешности.
Если значения погрешностей в точках
отсчета образуют стационарную последовательность, то ![]() .
.
При этом возможно спектральное
представление погрешности, если выразить корреляционную матрицу ![]() через спектральную плотность
погрешности
через спектральную плотность
погрешности ![]() в соответствии с теоремой
Хинчина-Винера:
в соответствии с теоремой
Хинчина-Винера:
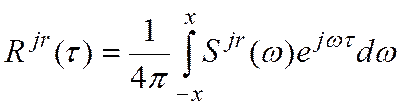 .
.
Тогда для дисперсии погрешности из выражения (10) получим
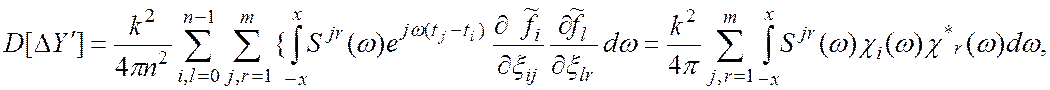 (14)
(14)
где 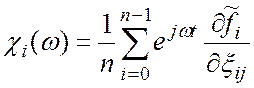 ;
;
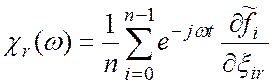 ;
;
*– знак комплексного сопряжения.
Если отдельные составляющие погрешности не коррелированны, то для дисперсии погрешности справедливо соотношение (11), при этом формула (14) имеет вид
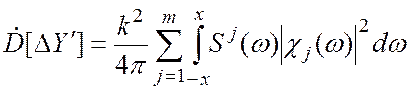 ,
,
где ![]() –
спектральная плотность j-й составляющей.
–
спектральная плотность j-й составляющей.
Приведенные выше соотношения позволяет вычислить статистические оценки погрешностей – математическое ожидание и дисперсию для всех алгоритмах ЦОС. При вычислении дисперсии можно пользоваться либо временным, либо спектральным преставлением. Спектральный метод может оказаться более удобным, в особенности при исследовании влияния внешних помех, так как он позволяет более наглядно и четко выделить частотный диапазон помех, приводящий к наиболее слабой помехоустойчивости данного алгоритма ЦОС, и исследовать погрешности именно в этом диапазоне. С другой стороны, из экспериментальных данных можно получить матрицу корреляций погрешности. В этом случае возможно два пути. Один из них состоит в переходе от корреляционных функций, заданных аналитически или графически, к спектральной плотности, а другой путь – в непосредственном использовании формул статистических оценок, содержащих матрицы корреляции погрешностей. По объему вычислений временной (корреляционный) и спектральный методы отличаются несущественно.
[Чинков В.Н. Цифровая обработка сигналов в измерительной технике: Методические основы оценки погрешностей// Украiнський метрологiчний журнал.–2000.–Вип 4.–стр. 18-21].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.