Государственное образовательное учреждение высшего профессионального образования «Мордовский государственный университет им. Н.П. Огарева»
Кафедра Государственного и муниципального управления
1. Применение метода ARIMA для прогнозирования показателей торгового баланса.
2. Применение метода экспоненциальное сглаживание для прогнозирования показателей безработицы.
Студентки экономического факультета 4 курса 419 группы
Саниной Натальи Владимировны
Проверил к.э.н., старший преподаватель
Черемушкин Сергей Васильевич
Саранск 2006 г.
1. Исходными данными для прогнозирования являются показатели сальда торгового баланса в РФ за период с 1997 по 2006. Данные представлены по месяцам, в млн. долл. США (подробнее см. таблицу 1.)
Цель работы: изучить данные по внешнеторговому балансу в Российской Федерации и составить прогноз на конец 2006 года и на 2007 год включительно.
Прежде чем приступить к построению модели необходимо построить и оценить график переменной. Он представлен на рисунке 1. Можно сказать, что прогнозируемый параметр не имеет четко выраженной сезонной структуры, динамика показателя имеет возрастающий тренд, отсутствует гетероскедастичность. Таким образом, для прогнозирования мы имеем нестационарный ряд, который требует преобразования.
Для преобразования мы возьмем разность с лагом 1 два раза и с лагом 12 один раз (так как существует возможность некоторой сезонности в данных), в результате исходный ряд данных приобретет вид стационарного ряда (см. рисунок 2.)
Для определения типа модели необходимо обратиться к функциям автокорреляции и частной автокорреляции (см. соответственно рисунки 3 и 4). На рисунке 3 отчетливо видно, что функция автокорреляции обрывается на лаге 1 – параметр q, функция частной автокорреляции также обрывается, но на лаге 4 – параметр p. Как нам известно, если функции автокорреляции и частной автокорреляции обрываются, то можно использовать любую модель. Мы решили использовать модель ARIMA.
При задании модели с параметрами q=1, p=4 обнаруживается, что два параметра p статистически не значимы, следовательно, их необходимо убрать. Зато при добавлении параметра сезонной составляющей qs – обнаруживаем его статистическую значимость. В конечном итоге для прогнозирования мы имеем модель со следующими характеристиками (2,2,1)U(0,1,1). Теперь необходимо задать период прогнозирования, в нашем случае он равен 16 месяцам.
В результате запуска программы получим следующий прогноз (подробнее рисунок 5 и таблицу 2).
Для верификации модели необходимо провести проверку функции автокорреляции остатков, главный критерий адекватности модели – параметр χ2, который должен быть не статистически значимым на всех лагах. Функция автокорреляции остатков представлена на рисунке 6, как видно, все остатки статистически не значимы из чего можно сделать вывод о правильности и адекватности выбранной модели.
Рисунок – 1.
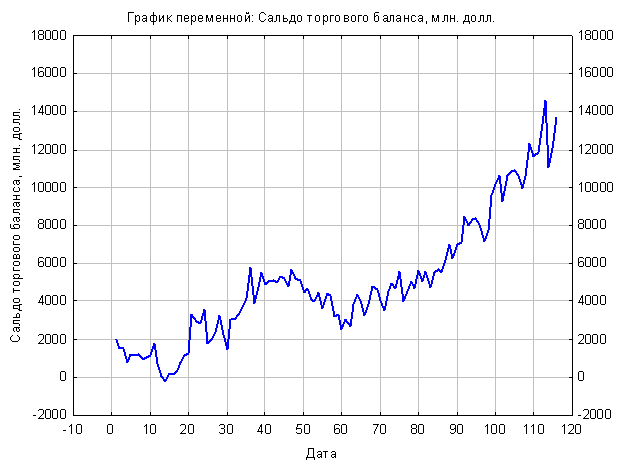
Рисунок – 2.
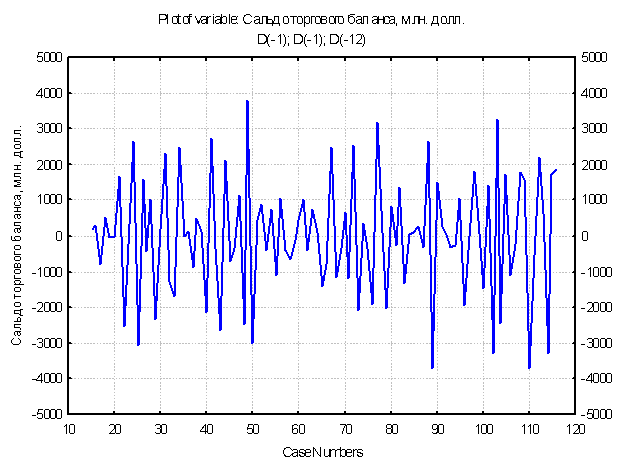 |
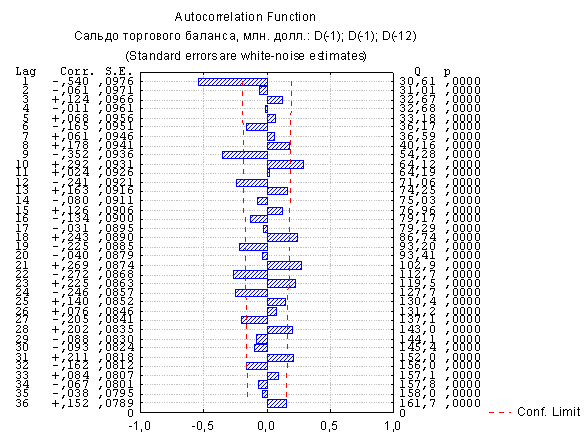 Рисунок – 3.
Рисунок – 3.
Рисунок – 4.
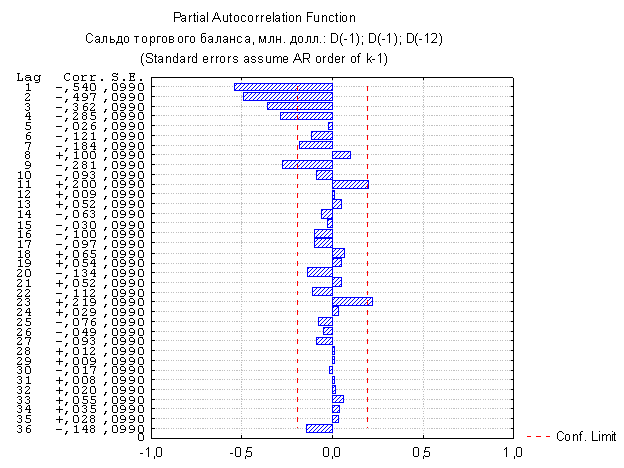 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.