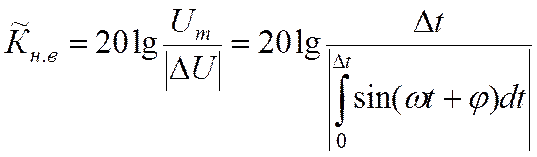Помехозащищенность цифрового вольтметра, страница 6

                                                                                (30).

Введем обозначение

                                              m=/T=f                       (31),

где T и f – период и частота помехи.

Используя это обозначение и взяв интеграл в (30), получаем

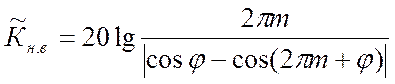                                                                                (32).

Таким образом,  зависит от m и . Интерес представляет значение  при худшем . Выражение для  можно получить обычным способом поиска экстремума:

Решить относительно  уравнение ;

Подставит полученное наихудшее = в (32).

Можно, однако, получить результат менее строгим, но более простым и наглядным путем.

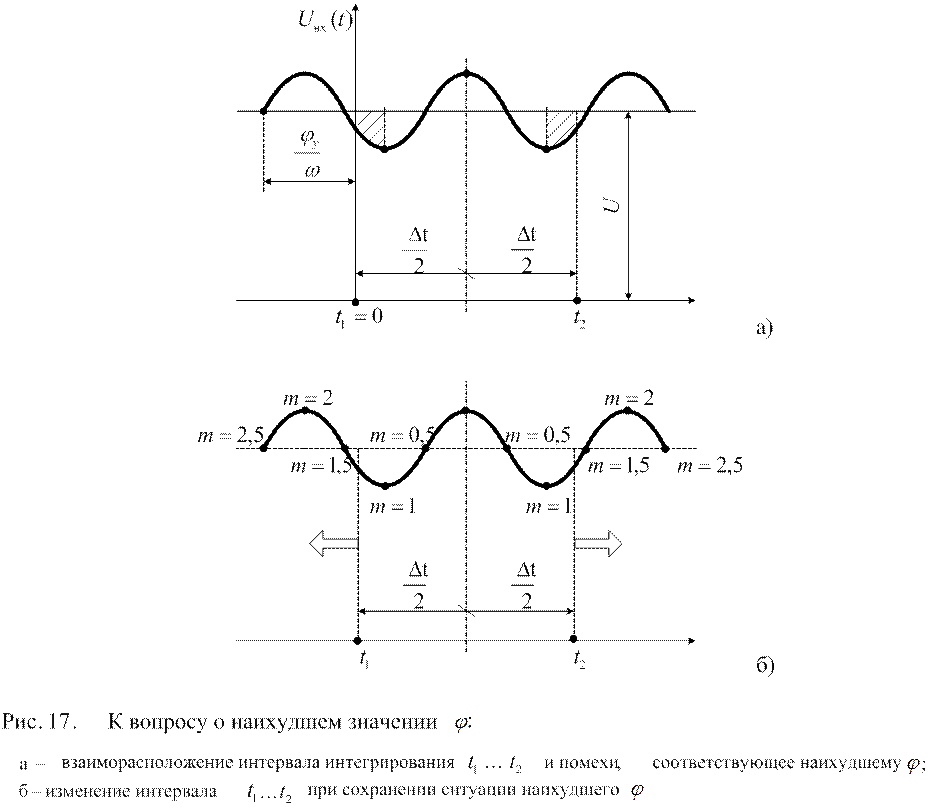
Из рис. 17,а ясно, что представленное на нем взаиморасположение интервала интегрирование  и помехи соответствуют наихудшей фазе. При таком взаиморасположении максимальна площадь заштрихованных участков, а ей соответствуют . Действительно, любое смещение интервала интегрирования вправо или влево при неизменном положение синусоиды уменьшит эту площадь.

Таким образом, наихудшее значение = - это такое, при котором середина интервала интегрирования попадает на экстремум синусоиды-помехи ( на рис. 17,а – на максимум).

Легко себе представить и наилучшее , при котором середина интервала интегрирования попадает на нулевое значение синусоиды. В этом случае =0 и →∞. Далее, зная, что рис. 17,а соответствует = непосредственно по (30). Для этого сначала, мысленно перенося ось ординат в точку , запишем очевидное равенство

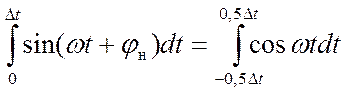                                                                                          (33).

Вычисление правой части (33) с использованием обозначения (31) и подстановка полученного результат в (30) с учетом равенства (33) дают

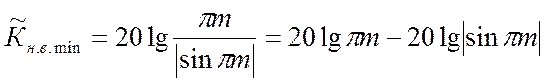                                                         (34).

Таким образом,  зависит только от m.

При целочислительных значениях m имеем sin =0 и →∞. Напомним, что индекс min показывает, что  зависит от  и при худшем = этот коэффициент минимален. Однако при целочислительных значениях  m коэффициент →∞ при любом , в том числе и при  =.

В более наглядной форме сказанное представлено на рис. 17,б. Сдвигая или раздвигая границы интервала интегрирования , но оставляя этот интервал симметричным относительно экстремума помехи, тем самым задаем различные значения m, сохраняя ситуацию наихудшего . Когда при этом границы совпадают с экстремумами синусоиды, интеграл от нее  на данном интервале обращается в нуль, что соответствует →∞. Таким образом, целочисленные числа m являются наилучшими.

При дробных значениях m=0,5; 1,5; 2,5 …, как видно из рис. 17,б, интервал помехи максимален. При этом =1 и в соответствии с (34)

                                                                                                                    (35)

Это выражение представляет собой уравнение прямой, на которой находятся значения  при самом неблагоприятном значении  и m=0,5; 1,5; 2,5 … Эта прямая проходит через точку m =1/ и имеет наклон +20 дБ/дек.

Зависимость (m) показана на рис. 18,а. Она ограничивает снизу бесчисленное множество значений : при любом m коэффициент  может принимать любые значения от ∞ до .

На первый взгляд значения m=0,5; 1,5; 2,5 … как раз и являются наихудшими, ибо они соответствуют максимума интеграла помехи (рис. 17,б). В действительности это не совсем так: важен не сам интеграл помехи, а усредненный за время интеграл (см. (26)). По рис. 17,б можно качественно представить себе следующее. Раздвигая границы интервала  и подходя к точкам m=0,5; 1,5; 2,5 …, видим, что при этом площадь синусоиды, т.е. интеграл помехи, нарастает медленнее, чем интервал . Это значит, что наихудшие значения m располагаются где-то вблизи значений m=0,5; 1,5; 2,5 …, но они несколько меньше этих значений.

Для нахождения этих наихудших значений m нужно найти корни уравнения

                                              ,

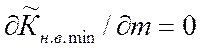где  определяется (34). Производная от (34) дает трансцендентное уравнение

                                                          

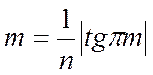
корни которого можно найти численным методом: m=1,43; 2,46; 3,47; …

Как видим, с увеличением m эти наихудшие значения приближаются к значениям m=0,5; 1,5; 2,5; 3,5 … Подстановка найденных наихудших значений m в (34) позволяет определить ординаты минимумов функции : 13,3 дБ; 17,8 дБ; 20,8 дБ; … С увеличением m их отличие от ординат касания точек касания при m=0,5; 1,5; 2,5; … соответственно составляет 2,4

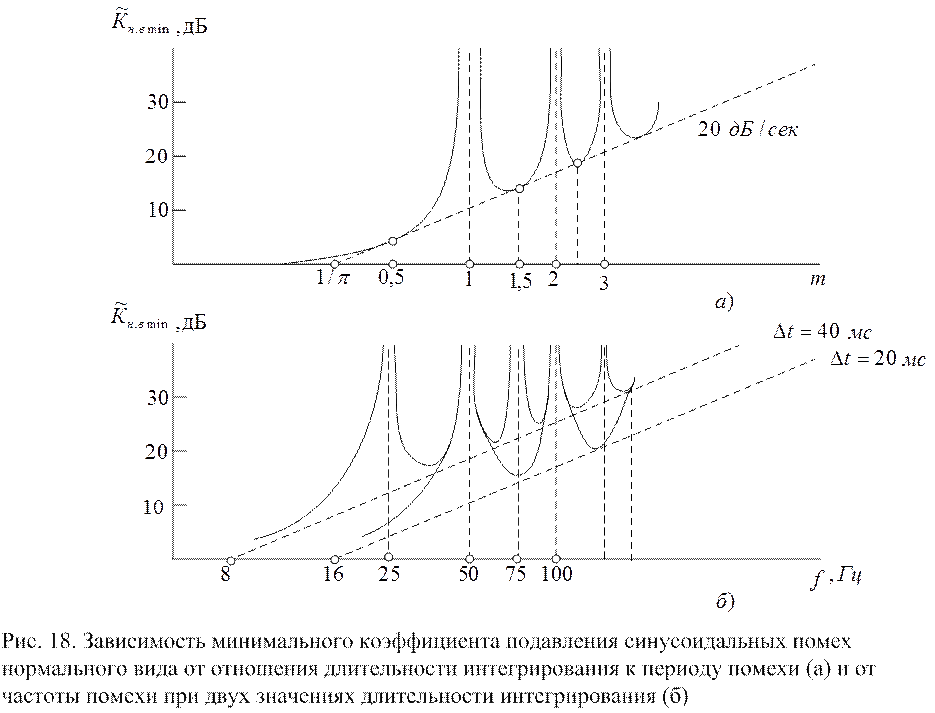
%; 0,84 %; 0,57 %; …, т.е. тоже убывает. Таким образом, с увеличением m координаты минимумов приближаются к координатам точек касания. Пренебрегая различием между ними, можно пользоваться простым выражением (35), считая, что оно определяет нижнюю границу значений  при самых неблагоприятных значениях  и m.

Большой практический интерес представляют значения  при малых отступлениях от равенства (31), т.е. в небольших окрестностях целочисленных значений m.

Введем обозначение

                                                         m=k(1±),

где k=1,2,3 … (точно); <<1.

Тогда в соответствии с (34)

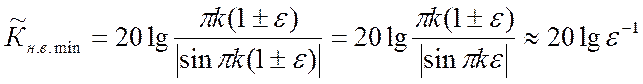                              (36).

Таким образом, при малых отклонениях от равенства или кратности между интервалом интегрирования  и периодом помехи T значение  определяется только значением относительно расхождения  между  и Т и не зависит от значения .

Пример. =20 мс; f=50±0,5 Гц. В этом случае m=1±0,001, т.е. k=1 и =0,01 и =20 lg 100 = 40 дБ.

Для получения больших значений  иногда применяют автоподстройку длительности  под изменяющуюся частоту сети.