Помехозащищенность цифрового вольтметра, страница 4

Как входное (), так и выходное () напряжение фильтра FF содержит полезные составляющие (,), обусловленные измеряемым напряжением постоянного тока U, и вредные синусоидальные составляющие (,), обусловленные  и . Смысл фильтрации заключается в различии коэффициентов преобразования / и /; полезный сигнал  почти не уменьшается или даже усиливается ( при активном фильтре), а вредный сигнал  в определенном диапазоне частот ослабляется. Степень подавления вредного сигнала фильтром  характеризуют коэффициентом фильтрации.

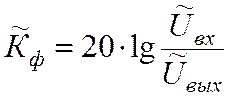                                                            (17)

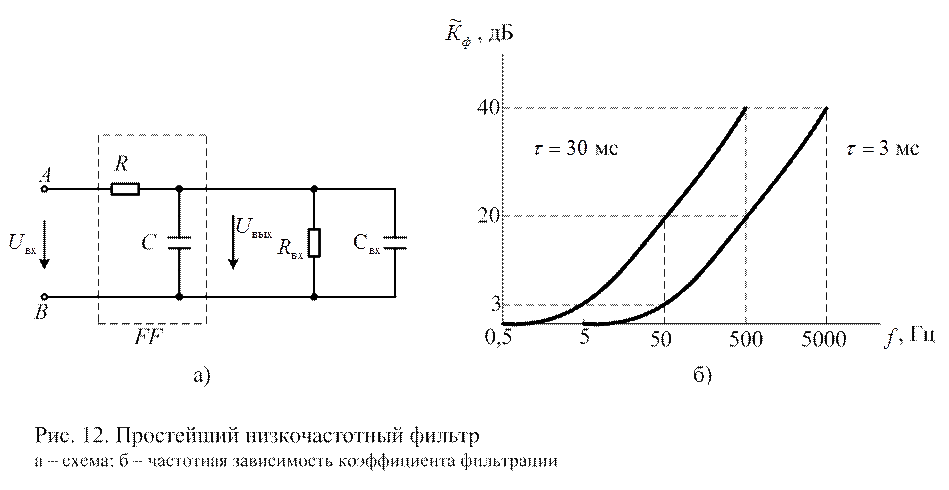
На рис. 12,а показан простейший низкочастотный RC-фильтр. Входная цепь последующего звена, например усилителя, представлена в виде параллельного соединения   и .

 

Обычно <<C, поэтому ее можно не учитывать. Если выбрать R<<, то фильтр почти не будет ослаблять полезную составляющую входного напряжения:

                                              .

          Не составляет труда выразить в соответствии с (17) коэффициент подавления вредной составляющей . Пренебрегая шунтирующим действием , получаем

                                   ,

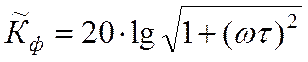где  - постоянная времени фильтра.

При

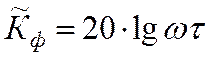                                          ,                    (18)

т.е. частотная зависимость  в логарифмическом масштабе по оси абсцисс представляет собой прямую линию с наклоном +20 дБ/дек.

 В полосе пропускания фильтра при  имеем . Границей полосы пропускания условно считают частоту , при которой , т.е. . При этом

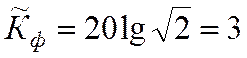                                     дБ.

На рис. 12,б показана частотная зависимость  для двух значений . Таким образом, низкочастотный фильтр тем лучше защищает ЦВ от помехи, чем выше его частота. Для защиты от помех сетевой частоты он мало выгоден. Из рис. 12,б видно, что для повышения значения  на частоте 50 Гц нужно значительно увеличить . Увеличение  ограничено возрастанием инерционности для полезного сигнала: помехозащищенность и быстродействие находятся в противоречии. Допустим, что отсутствуют, а измеряемое напряжение изменилось скачком от 0 до . Тогда выходное напряжение фильтра будет изменяться по экспоненциальному закону

                                 .

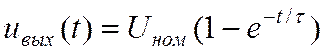Для получения правильного результата нужно «дождаться», пока  достаточно приблизится к установившемуся значению. Если допустить отличие от установившегося значения в один квант q, то время установления  можно найти из условия

                       .

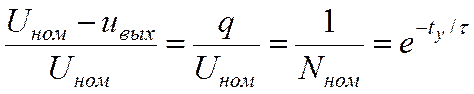Отсюда:

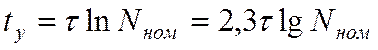                              .        (19)

Например, при  имеем . Чем больше ,т.е. чем больше , тем больше , т.е. тем меньше быстродействие.

 

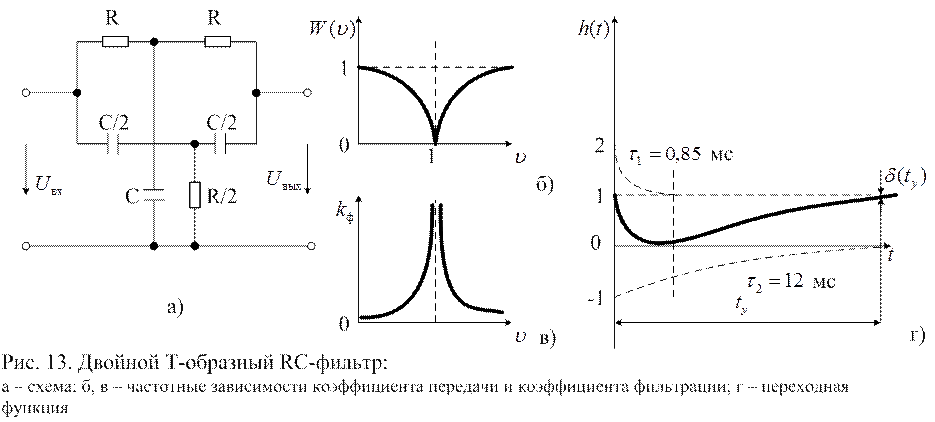
Кроме того, увеличение  путем увеличения С ограниченного габаритами конденсатора и целым рядом недостатков, связанных с применением конденсатора большей емкости. Увеличение  путем увеличения R ограничено теми же факторами, которые ограничивают значения  источника измеряемого напряжения. Если принять R=1 кОм, то даже при C=100 мкФ на частоте 50 Гц получим всего лишь =30 дБ, а время установления при   будет около 1с.

Поэтому для защиты от помех сетевой частоты применяют более сложные режекторные (заграждающие) фильтры. В качестве примера такого фильтра на рис. 13,а показан так называемый двойной Т-образный RC-фильтр.

Полагая, что выходное сопротивление источника сигнала близко к нулю, а сопротивление нагрузки фильтра (входное сопротивление усилителя) близок бесконечности, можно показать, что передаточная функция фильтра определяется выражением

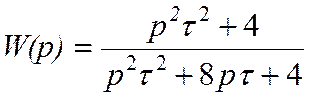                                               (20),

где .

Схема на рис. 13,а представляет собой шестиплечий мост. При  на определенной частоте, называемой частотой настройки и определяемой выражением

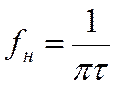                                                                            (21)

этот мост уравновешен, т.е. .

Для настройки на частоту 50 Гц нужно обеспечить

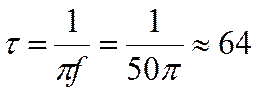                                                    мс,

выбрав, например R=1 кОм и С=6,4 мкФ.

Введя безмерную частоту

                                                         ,

определим модуль комплексного коэффициента передачи, пользуясь (20) и (21):

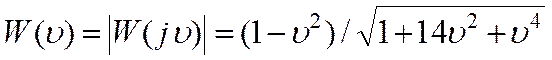                                                                               (22).

Рассмотрим три характерные точки:

1.  ; ; , т. е. .

Физически это легко представить, отбросив конденсаторы в схеме на рис 13,а;

2.  ; ;, т. е.  . Это соответствует балансу моста

3.  ; ; , т.е. снова . Это можно представить, закоротив конденсаторы в схеме на рис. 13,а. Зависимость  показана на рис. 13,б. В соответствии с (17)

.

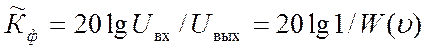Зависимость показана на рис. 13,в. Интерес представляют значения  при малых отклонениях частоты помехи f от частоты настройки фильтра :

; ,

или

; ; .

Из (22) следует, что в этом случае

.

Соответственно

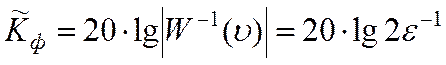                           (23).

Пример. =50 Гц; f=50 Гц0,5 Гц. При этом e=0.01 и  дБ. Оценим теперь инерционность этого фильтра.

При действии на входе фильтра напряжения, изменяющегося скачком от 0 до E, т.е. при

  

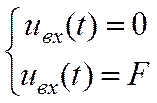
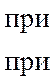
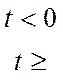
на выходе образуется реакция на этот скачок , являющаяся оригиналом изображения по Лапласу функции :

~,

причем

                                                (24)

и

.

Последнее выражение представляет собой изображение по Лапласу постоянной величины E.

Подставив (20) и (25) в (24) и приведя его к табличному виду, получаем

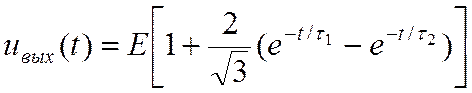                       . (26)

где ; .

При = 50 Гц и , следовательно, =6,4 мс имеем =0,85 мс и =12 мс.

Подставляя эти значения в (26) и учитывая, что переходная функция определяется отношением

,

получаем

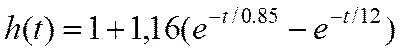                            ,      (27)

где t-время в миллисекундах.

Рассмотрим две характерные точки:

1) ; h(∞)=1, т.е. .